XiaoMi-AI文件搜索系统
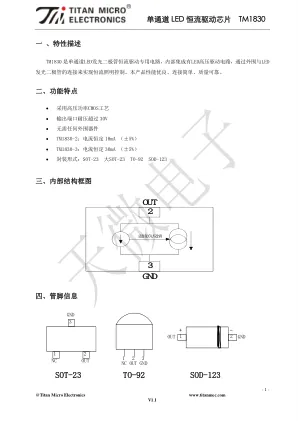
World File Search System单通道LED 恒流驱动芯片TM1830
如图1 所示,要使TM1830 工作在恒流状态下,芯片OUT 引脚上电压应大于2.2V,即芯片的2、3 脚之间的电压应达到2.2V 以上。在应用时,电源串接LED 灯后加在OUT 引脚上的电压建议在3.0V 左右。 如果芯片持续工作在额定恒流状态下,TM1830-2 和TM1830-3 的OUT 引脚电压应分别在12.0V 和8.0V 以内为宜。
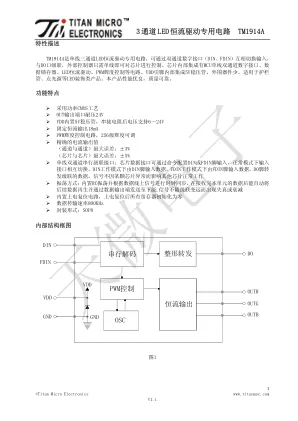
3通道LED恒流驱动专用电路TM1914A
功能说明 1、模式设置 本芯片为单线双通道通讯,采用归一码的方式发送信号。芯片接收显示数据前需要配置正确的工作 模式,选择接收显示数据的方式。模式设置命令共48bit,其中前24bit为命令码,后24bit为检验反码, 芯片复位开始接收数据,模式设置命令共有如下3种: (1)0xFFFFFF_000000命令: 芯片配置为正常工作模式。在此模式下,首次默认DIN接收显示数据,芯片检测到该端口有信号输 入则一直保持该端口接收,如果超过300ms未接收到数据,则切换到FDIN接收显示数据,芯片检测到该 端口有信号输入则一直保持该端口接收,如果超过300ms未接收到数据,则再次切换到DIN接收显示数据。 DIN和FDIN依此循环切换,接收显示数据。 (2)0xFFFFFA_000005命令: 芯片配置为DIN工作模式。在此模式下,芯片只接收DIN端输入的显示数据,FDIN端数据无效。 (3)0xFFFFF5_00000A命令: 芯片配置为FDIN工作模式。在此模式下,芯片只接收FDIN端输入的显示数据,DIN端数据无效。 2、显示数据
WS9032G 非隔离降压型LED 恒流驱动芯片 - NET
X-ON Electronics Largest Supplier of Electrical and Electronic Components Click to view similar products for LED Display Drivers category: Click to view products by Winsemi manufacturer: Other Similar products are found below :
WS9056X 非隔离降压型LED 恒流驱动芯片 - NET
X-ON Electronics 最大的电气和电子元件供应商 点击查看 LED 显示驱动器类别的类似产品: 点击查看 Winsemi 制造商的产品: 其他 类似产品如下:
黎曼方法与卷积神经网络
摘要 目的。迄今为止,在基于 EEG 的脑机接口中,黎曼解码方法与深度卷积神经网络的全面比较仍未在已发表的研究中出现。我们使用 MOABB(所有 BCI 基准之母)来解决这一研究空白,将新型卷积神经网络与最先进的黎曼方法进行比较,这些方法涉及广泛的 EEG 数据集,包括运动想象、P300 和稳态视觉诱发电位范式。方法。我们使用 MOABB 处理管道系统地评估了卷积神经网络(特别是 EEGNet、浅层 ConvNet 和深度 ConvNet)与成熟的黎曼解码方法的性能。该评估包括会话内、跨会话和跨受试者方法,以提供模型有效性的实用分析,并找到在不同实验设置中表现良好的整体解决方案。主要结果。我们发现在会话内、跨会话和跨受试者分析中,卷积神经网络和黎曼方法之间的解码性能没有显着差异。意义。结果表明,在使用传统的脑机接口范式时,在许多实验环境中,CNN 和黎曼方法之间的选择可能不会对解码性能产生重大影响。这些发现为研究人员提供了灵活性,可以根据诸如易于实施、计算效率或个人偏好等因素选择解码方法。
黎曼流形上的差分隐私
在这项工作中,我们考虑了发布驻留在黎曼流形上的差分隐私统计摘要的问题。我们提出了拉普拉斯或 K 范数机制的扩展,该机制利用了流形上的固有距离和体积。我们还详细考虑了摘要是驻留在流形上的数据的 Fréchet 平均值的特定情况。我们证明了我们的机制是速率最优的,并且仅取决于流形的维度,而不取决于任何环境空间的维度,同时还展示了忽略流形结构如何降低净化摘要的效用。我们用两个在统计学中特别有趣的例子来说明我们的框架:对称正定矩阵的空间,用于协方差矩阵,以及球面,可用作离散分布建模的空间。
黎曼切线空间的迁移学习
摘要 — 使用迁移学习来训练脑机接口 (BCI) 解码算法有助于减少校准时间、提高准确性、降低过度拟合风险并允许应用需要大量数据的机器学习方法,例如深度神经网络。在本文中,我们提出了一种受黎曼几何最新进展启发的迁移学习方法。该方法通过 Procrustes 分析在源和目标数据集的切线空间中对齐向量。我们将该方法应用于公开的 P300-BCI 数据库。我们表明,使用我们的方法可以重用来自其他受试者的数据来传输信息。与最先进技术相比,我们获得的分类准确性表明使用迁移学习方法可以清晰地传输信息。
R-Mixup:生物网络的黎曼混合
生物网络通常用于生物医学和医疗保健领域,以有效地模拟复杂生物系统的结构以及连接生物实体的相互作用。然而,由于其高维和低样本量的特点,直接将深度学习模型应用于生物网络通常会面临严重的过拟合。在本文中,我们提出了一种基于 Mixup 的数据增强技术 R-Mixup,它适合生物网络邻接矩阵的对称正定 (SPD) 性质,并优化了训练效率。R-Mixup 中的插值过程利用了黎曼流形中的对数欧几里德距离度量,有效地解决了 vanilla Mixup 的膨胀效应和任意错误的标签问题。我们用五个真实的生物网络数据集在回归和分类任务上证明了 R-Mixup 的有效性。此外,我们推导出一个常被忽视的识别生物网络 SPD 矩阵的必要条件,并实证研究了其对模型性能的影响。代码实现可以在附录E中找到。