XiaoMi-AI文件搜索系统
World File Search System真空和不均匀的Abelian Higgs模型
对Bogomolny-Prasad-Sommerfield(BPS)限制的不均匀的Abelian Higgs模型均针对相对论和非遗体主义制度研究了。尽管空间翻译的对称性因不均匀性而破坏,但延伸到N¼1超对称理论。四分之一的标量电势具有最小值,具体取决于杂质的强度,但在空间渐近线下具有破碎的相位。破碎相的真空构型既不是常数也不是标量电势的最小值,而是被发现是bogomolny方程的非平凡解。虽然其能量密度和磁场是由空间坐标的功能给出的,但能量和磁通量保持为零。磁杂质项的符号允许BPS扇区或抗BPS扇区,但不能同时进行。因此,所获得的溶液被确定为最小零能量的新型不均匀损坏的真空。在存在旋转对称的高斯类型不均匀性的情况下,还获得了拓扑涡流溶液,并且对杂质对涡流的影响进行了数值分析。
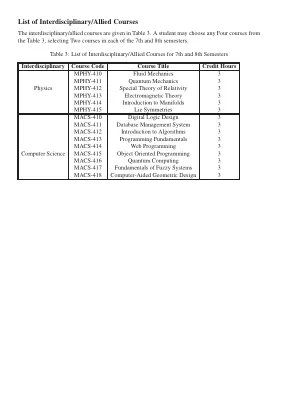
跨学科/相关课程列表
静磁场:磁静力定律、磁感应、磁场中运动的点电荷所受的洛伦兹力、磁场的发散、矢势、电荷守恒和连续性方程、洛伦兹条件、磁场的旋度、安培定律和标量势。
3D光子Chern绝缘子的矢量散装对应关系
组的(保守的)分量(保守的)速度正常与磁化轴(即Chern矢量方向)具有良好的符号,并且表面状态不能沿该特定方向向后散射。在2D中,Chern矢量始终沿缩小尺寸的轴固定,即与系统平面正交的固定。因此,它可以被视为标量数量:Chern数字C,其特征是2D顺式的大量拓扑。[7-9]在这种情况下,可以定义散装对应关系(SBBC)的“标量”范围,以将批量拓扑连接到边界模式的数量。[10,11]根据2D CIS中的SBBC,两个具有Chern数字C 1,C 2的系统之间的接口具有N E = | C 1 -C 2 |受保护的手性边缘状态。这意味着只有在界面上的Chern数字的连续性的情况下,手性边缘状态才能出现,即C 1≠c 2。[12–15]
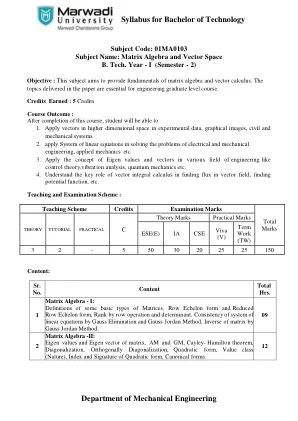
技术学士学位课程大纲...
向量微积分:回顾向量代数的概念、标量和向量函数、梯度散度和旋度、方向导数、保守向量场、无旋函数和螺线函数。线积分、线积分的路径独立性、曲面积分的概念、格林定理、斯托克斯定理和散度定理。
纠缠在量子场论中到底有多普遍?
众所周知,纠缠在量子场论中广泛存在,具体含义为:每个 Reeh-Schlieder 态都包含任意两个空间分离区域之间的纠缠。这尤其适用于闵可夫斯基时空中无相互作用的标量理论的真空。场论中关于纠缠的讨论主要集中在包含无限多个自由度的子系统上 — — 通常是在紧凑空间区域内支持的场模式。在本文中,我们研究 D + 1 维闵可夫斯基时空中的自由标量理论中由有限个场自由度组成的子系统中的纠缠。关注场的有限个模式是受真实实验有限能力的驱使。我们发现有限维子系统之间的纠缠并不常见,需要仔细选择模式的支持才能出现纠缠。我们还发现纠缠在高维中越来越稀疏。我们得出结论,闵可夫斯基时空中的纠缠并不像通常认为的那么普遍。
动态暗能量模型
在研究的第一部分,我们将暗能量建模为一个标量场,该标量场可以最小或非最小耦合到 Ricci 标量,并给出了宇宙场方程的多个精确解。每个解都对应一种特定的几何形状 — — 平坦、开放或封闭。在下一部分中,我们将分析方法与数值技术相结合,对文献中的几种模型进行分析,这些模型之所以被选中,是因为它们能够代表完整的宇宙历史。目的是研究空间曲率如何影响演化的主要特征。最初,我们假设宇宙由范德华流体组成,但仅凭这一点无法解释后期的加速现象,尽管它解释了膨胀和物质主导的时期。因此,我们将暗能量作为精髓、恰普雷金气体或动态真空能量引入。事实证明,从膨胀时期到物质主导时期的转变将首先发生在开放宇宙中,最后发生在封闭宇宙中。晚期加速的开始也将按此顺序发生。此外,发现正曲率
时空光学涡旋:描述原理和基本性质
本汇编总结了时空光学涡旋 (STOV) 结构和特性的主要物理基础。描述和表征 STOV 的一般方法基于标量近轴高斯波包模型。在此基础上,任意阶的 STOV 结构被视为时空厄米-高斯模式的叠加。这种方法能够以明确且物理透明的形式系统地表征主要的 STOV 特性。特别是,我们分析了 STOV 振幅和相位分布、它们在自由传播和光学系统中的演变、内部能量流和轨道角动量。讨论并定性解释了拓扑决定的 STOV 固有不对称性以及“能量中心”和“概率中心”之间的差异 [Phys. Rev. A 107 , L031501 (2023)]。概述了 STOV 生成和诊断方法,并简要描述了非高斯(贝塞尔型)STOV 的主要特性。最后,考虑了整个文本中接受的标量高斯模型的局限性,并揭示了可能的概括。整个演示可能有助于初步介绍与 STOV 相关的思想及其非凡的特性。
学术手册
平均值定理的重要性及其应用,评估多个积分,具有物理理解的矢量演算语言,可以处理诸如流体动力学和电磁场等受试者,序列和系列和系列的融合以及傅立叶系列。模块1差分微积分12小时的限制,连续性和不同性;平均值定理,泰勒和麦克劳林的定理,部分分化,总分分化,欧拉的定理和概括,最大值和最小值的几个变量功能,Lagrange的乘数方法;变量的变化 - 雅各布人。模块2积分10小时的微积分基本定理,不当积分,面积的应用,体积。双重和三个积分模块3矢量计算14标量和向量场;向量分化;定向衍生物 - 标量场的梯度;向量场的发散和卷曲 - 拉普拉斯 - 线和表面积分;格林在飞机上的定理;高斯分歧定理;斯托克斯定理。模块4序列和串联10小时
光子学
•射线射线光学光学(几何(几何光学)光学):: Fermat的Fermat的Fermat的原理,原理,原理,携带携带和矩阵矩阵光学元件.. s l s l s l s l s l s l s l s l w o ti o ti o ti(i t f&g i g i g i g i s claverian scressic corterican s clave and clave scallice sclasic scallice scallice clave and clave wave wave wave wave( Beams) Beams): Scalar Scalar wave wave equation, equation, Helmholtz Helmholtz equation, equation, Superpostion Superpostion of of Waves, Waves, Interferometers, Interferometers, Paraxial Paraxial Wave Wave Equation, Equation, Gaussian Gaussian Beam Beam Solution, Solution, ABCD ABCD Law, Law, Hermite Hermite-Gaussian Gaussian Beams Beams.ABCD ABCD法律,法律,Hermite Hermite高斯高斯横梁。•激光激光物理物理学:轻度放大,放大,抽水计划,方案,增益系数,系数,系数,激光激光输出(CW(CW(CW和脉冲)脉冲)。声音大声疾呼,光学和非线性非线性光学元件• Electromagnetic Electromagnetic Optics Optics:: Maxwell Maxwell Equations Equations in in Vacuum Vacuum and and Dielectrics, Dielectrics, Monochromatic Monochromatic Waves, Waves, Plane Plane Waves, Waves, Polarization Polarization Ellipse, Ellipse, Jones Jones Formalism, Formalism, Reflection Reflection and and Refraction Refraction of of Light Light from from aa Boundary边界..•Fabry Fabry-孔孔洞腔::平面平面腔,腔,阻尼,阻尼,技巧,技巧,技巧,球形球形 - 镜面镜面腔,腔,稳定稳定和不稳定的不稳定型腔。光学光学涂层涂层设计•光子光子光学光学和光材料 - 物质材料相互作用::光子光子光子和光子光子流式流式材料材料属性属性,并模型模型光子光子和原子和原子和原子和原子流,以及流,材料,材料材料属性以及模型,模型,模型,模型,模型,光子,光子光子和型号。
AQA GCSE三部曲科学:如何成功!
•标量和矢量数量,接触和非接触力,重力,导致力,工作和能量传递,力和弹性,距离和位移,速度和位移,速度,速度,距离,距离时间图,加速度,牛顿的第一,第二和第三法律,力量,力量和制动 - 影响停止距离的距离,和反应时间和反应时间,较高的动量,仅(更高)(较高)(较高)(较高)(仅)6。波;