XiaoMi-AI文件搜索系统
World File Search System复合 - 弗里米昂在半填充和四分之一...
在半填充的最低兰道水平上,Halperin-Lee-Lee读的复合材料式费米斯是一个引人入胜的金属相,它是从电子的角度出发的强烈相关的“非Fermi液体”。值得注意的是,实验发现,随着量子井的宽度增加,该状态将过渡到分数量子霍尔状态,自从三十多年前发现以来,其起源一直是一个重要的难题。我们使用系统的变分框架进行详细而准确的定量计算,以配合复合费米子的配对,这些框架紧密模仿了Bardeen-Cooper-Schrieffer超导性的理论。我们的计算表明(i)随着量子 - 孔宽度的增加,占据量子的最低对称子带的单个成分复合材料费米式海洋井口将不稳定置于单一组件p-波配对的复合材料材料状态; (ii)量子孔宽度 - 电子密度平面中的理论相图与实验非常吻合; (iii)量子井的电荷分布中有足够数量的不对称性破坏了分数量子霍尔的效应,如实验性观察到的; (iv)两个组件331状态在能量上比单个组件配对状态的好处。在四分之一填充的最低兰道水平的宽量子井中已经看到了分数量子厅效应的证据;在这里,我们的计算表明复合费米子的F波配对状态。提到了各种实验意义。我们进一步研究了等于一个的填充因子的最低兰道水平的玻色子,并表明复合费米子的p波配对不稳定性,它们是携带单个通量量子的玻色子,对于短范围以及库仑的相互作用,都与精确的直径研究一致。通过实验的复合 - 弗里米亚 - schrieffer方法的一般一致性为偶数量指填充因子的分数量子霍尔效应的机制提供了支持的概念。
关于给定色数图中奇数圈的加强
我们遵循 [9, 13] 中的符号。设 G 为图。对于 V(G) 的非平凡划分 (A,B),1如果路径 P 的一端在 A 中而另一端在 B 中,则我们称路径 P 为 A - B 路径。设 P 为图 G 中的一条路径。设 | P | 为 P 中的边数。如果 | P | 为偶数(分别为奇数),则我们称 P 为偶数(分别为奇数)。设 C 为按循环顺序具有顶点 v 0 ,v 1 ,...,vt − 1 的环。设 C i,j 表示 C 的子路径 vivi +1...vj,其中索引取自加法群 Z t 。设 H 为 G 的子图。如果顶点 v ∈ V ( G ) − V ( H ) 在 G 中与 V ( H ) 中的某个顶点相邻,则我们称 H 和顶点 v ∈ V ( G ) − V ( H ) 在 G 中相邻。设 NG ( H ) = S v ∈ V ( H ) NG ( v ) − V ( H ) 且 NG [ H ] = NG ( H ) ∪ V ( H )。对于 S ⊆ V ( G ),如果 V ( G ′ ) = ( V ( G ) − S ) ∪{ s } 且 E ( G ′ ) = E ( G − S ) ∪{ vs : v ∈ V ( G ) − S 与 G 中的 S 相邻 } ,我们称图 G ′ 是通过将 S 收缩为顶点 s 而从 G 得到的。如果 G − v 包含至少两个分支,则连通图 G 的顶点 v 是 G 的割顶点。 G 中的块 B 是 G 的最大连通子图,使得不存在 B 的割顶点。注意块是孤立顶点、边或2连通图。G 中的端块是 G 中最多包含一个 G 的割顶点的块。如果 G 是图并且 x, y 是 G 的两个不同顶点,我们称 ( G, x, y ) 为有根图。有根图 ( G, x, y ) 的最小度为 min { d G ( v ) : v ∈ V ( G ) −{ x, y }} 。如果 G + xy 是2连通的,我们还称有根图 ( G, x, y ) 是2连通的。我们称 k 条路径或 k 条循环 P 1 , P 2 , . . . , P k 为
玻色-量子中的自旋动量纠缠
造成量子非局域性和违反贝尔不等式的原因。3纠缠一直是量子信息技术和工艺发展的重要资源。4–13 利用纠缠进行量子信息处理依赖于操纵量子系统的能力,无论是在气相还是固相中。在我们之前的工作中,我们研究了纠缠以及在光学捕获的极性和/或顺磁性分子阵列中进行量子计算的前景,这些分子的斯塔克能级或塞曼能级作为量子比特。13,14 在这里,我们考虑被限制在光阱中的 87 个 Rb 原子的玻色-爱因斯坦凝聚态 (BEC) 15,并研究其自旋和动量自由度之间的纠缠。原子的超精细塞曼能级及其量化动量可以作为量子比特,甚至是更高维的量子比特,即具有 d 维的量子比特。我们注意到,在气态系统中实现玻色-爱因斯坦凝聚态,随后又演示了自旋轨道耦合的玻色-爱因斯坦凝聚态 16,为量子控制开辟了新途径。在反应动力学的背景下,自旋轨道耦合
利用四波混频实现双色强度压缩
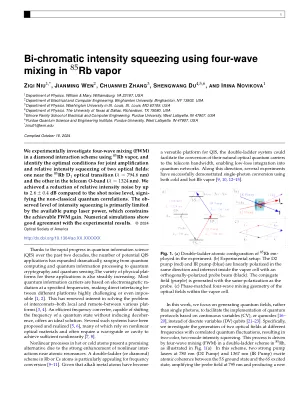
得益于过去 20 年量子信息科学 (QIS) 的快速发展,潜在的 QIS 应用数量急剧增加,包括量子计算和量子信息处理、量子密码和量子传感。这些应用的物理平台种类也在稳步增加。大多数量子信息载体基于特定频率的电磁辐射,因此不同平台之间的直接接口极具挑战性,甚至不可能实现 [1,2]。这重新引起了人们对解决不同平台之间本地和远程互连问题的兴趣 [3,4]。高效的频率转换器能够改变量子态的频率而不会引起退相干,因此提供了一种理想的解决方案。已经提出并实现了几个这样的系统 [5,6],其中许多依赖于非线性光学材料,并且通常需要波导或腔体来实现足够的非线性 [7,8]。热原子或冷原子中的非线性过程是一种很有前途的替代方案,因为原子共振附近的非线性相互作用得到了强烈的增强。Rb 或 Cs 原子中的双梯形(或菱形)方案对于频率转换特别有吸引力 [9-11]。鉴于碱金属原子已成为
多模捕获的干涉仪与非互操作玻色...
我们在实验上证明了一个多模干涉仪,其中包含一个被困在谐波电势中的39 K原子的玻色子凝结物,在该原子间相互作用中可以取消利用Feshbach的共振。kapitza-dirac从光学晶格中的衍射将BEC一致地分配在多个动量成分中,同样间隔,形成了不同的干涉路径,而轨迹被捕获的har-nonig势封闭。我们研究了两种不同的干涉方案,其中重组脉冲是在确定电位的全部或一半振荡后应用的。我们发现,干涉仪输出处动量成分的相对幅度通过诱导的谐波电位相对于光学晶格的诱导位移对外力敏感。我们展示了如何校准干涉仪,充分表征其输出并讨论透视改进。
国防部标准枪械术语(火炮)目录 NDS Y 0003B
3133 偏心螺钉式闭合装置 装弹孔与枪轴线处于同一位置,后膛环内的旋转中心与枪轴线偏心的一种安装在弹匣内并封闭枪管的闭合装置。通过旋转装载孔来打开腔室。用于外置冲锋枪等。
7. 垃圾填埋气收集系统设计和安装的最佳实践
场地条件和运营目标都会影响 GCS 的设计。场地条件(例如垃圾填埋场的几何形状、湿度、压实率、垃圾类型、垃圾深度、覆盖土壤的渗透性和最终覆盖层)都会影响 GCS 的设计。垃圾中的湿度越大,LFG 的生成速度就越快,峰值 LFG 生成率就越高。更快的 LFG 生成率还会导致垃圾沉降速度更快,这可能会对收集器造成损坏,可能需要对其进行评估并可能进行更换。垃圾中的液体可能会减少垃圾中的孔隙空间,从而降低 LFG 移动到 LFG 提取井的能力。因此,湿度较高的垃圾填埋场对单个收集器的有效影响半径(或影响区域)可能较小,并且可能需要更多的收集器才能覆盖相同的面积。相反,一些场地选择增加湿度以促进分解,这会增加 LFG 的生成,但可能会由于额外的井、增加的沉降和更大的集管尺寸而增加 GCS 的运营成本。
Final Cut Pro 中的 HDR 和广色域
多年来,专业摄像机中的图像传感器能够捕捉比 Rec. 709 更多的色彩和更高的动态范围。这些摄像机使用内部图像处理将输出色域和动态范围限制在广播行业标准 Rec. 709 范围内。最近,许多专业摄像机都采用了“log”、RAW 和 HLG 录制格式,这些格式既可以包含比 Rec. 709 色域更宽的色彩范围,又可以包含比 SDR 显示器上显示的更高的动态范围。随着 iPhone 12 及更高版本以杜比视界录制,HDR 捕捉不再仅限于专业摄像机的领域。
玻色-爱因斯坦凝聚态中涡旋的相位恢复
玻色-爱因斯坦凝聚态 (BEC) 是物质的一种量子态,其中玻色子粒子在单一本征态中形成宏观种群。预测这种状态的理论 [ 1 ] 等待了 70 年才在实验室中被探索 [ 2 , 3 ],这一里程碑式的成就开启了近 30 年在超冷原子和量子模拟器领域的卓有成效的研究 [ 4 ]。然而,尽管取得了进展,常用的 BEC 测量技术在提供的信息方面并不完整。成像是 BEC 测量技术的核心。通过将光照射穿过原子云并记录其投射的阴影,可以提取特定状态下原子的密度。通常有两种成像模式:原位,对仍在陷阱内的云进行成像,或飞行时间 (TOF)。后者通过打开陷阱并记录云膨胀后的原子密度来完成 [ 5 ];它类似于在光学中测量“远场”的强度。如果粒子在膨胀过程中不相互作用,并且云的初始尺寸相对于最终膨胀尺寸可以忽略不计,则 TOF 图像提供云的动量分布,即波函数的空间傅里叶变换的幅度。如果存在相互作用,但最终密度足够低,以至于它们可以忽略不计,则测量的动量分布的动能反映初始动能加上相互作用能。这些成像模式仅捕获状态的部分信息,因为它们仅在单个时间点和单个平面上测量密度,无论是原位还是 TOF。然而,BEC 是量子对象,因此它们是物质波 [6],其特征是振幅和相位。因此,要表征 BEC,必须在它们演化过程中获得其在空间中任何地方的振幅和相位的完整图。因此,依靠这两种模式,创新的
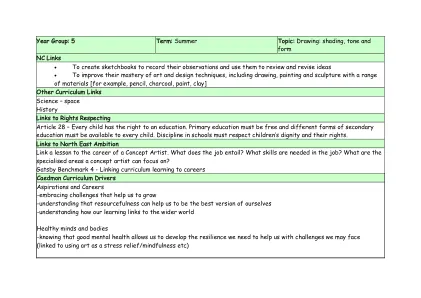
绘画:阴影、色调和形式 创建素描本以……
• 提高他们对艺术和设计技巧的掌握,包括使用各种材料(例如铅笔、木炭、油漆、粘土)进行绘画、绘画和雕塑 其他课程链接 科学 - 太空 历史 链接到尊重权利的第 28 条 - 每个儿童都有接受教育的权利。小学教育必须免费,每个孩子都必须接受不同形式的中学教育。学校的纪律必须尊重儿童的尊严和权利。 链接到东北雄心 将课程与概念艺术家的职业联系起来。这份工作需要做什么?这份工作需要什么技能?概念艺术家可以专注于哪些专业领域?盖茨比基准 4 - 将课程学习与职业联系起来