XiaoMi-AI文件搜索系统
World File Search System纠缠量子物理中的半拓扑数
在量子物理学中,拓扑相可以从自旋为 1/2 的布洛赫球面设计出来,该球面由于径向磁场而呈现出刺猬结构。我们详细阐述了在双自旋模型中,一极处纠缠波函数的形成与一对有趣的半拓扑数之间的关系。与超导体中的库珀对类似,一极处的爱因斯坦-波多尔斯基-罗森对或贝尔态产生半通量量子,这里指的是表面上贝里曲率的一半通量。这些 1/2 数字还指每个球面极点处存在自由马约拉纳费米子。当从北向南行驶时,以及从极点的圆极化场行驶时,可以测量拓扑响应,揭示受保护横向电流的量化或半量化性质。我们展示了纠缠波函数在能带结构中的应用,在动量空间中引入了一个局部标记,以表征双层几何中二维半金属的拓扑响应。
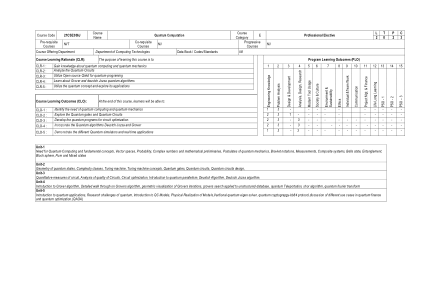
课程代码 21CSE306J 课程名称 量子...
单元 1 量子计算需求和基本概念、向量空间、概率、复数和数学预备知识、量子力学假设、Bra-ket 符号、测量、复合系统、贝尔态、纠缠、布洛赫球、纯态和混合态 单元 2 量子态的几何形状、复杂性类、图灵机、图灵机概念、量子门、量子电路、量子电路设计 单元 3 电路的定量测量、电路质量分析、电路优化、量子并行性简介、Deustch 算法、Deutsch Jozsa 算法 单元 4 Grover 算法简介、Grovers 算法详细介绍、Grovers 迭代的几何可视化、Grovers 搜索应用于非结构化数据库、量子隐形传态、Shor 算法、量子傅里叶变换 单元 5 量子应用简介、量子研究挑战、QC 模型简介、模型的物理实现、变分量子特征求解器、量子密码学-bb84协议,讨论量子金融和量子优化中的不同用例。(QAOA)
ELEC 361:工程师的量子力学
本课程为工程学本科生提供设计量子设备和系统(包括量子计算机)所需的物理理解和数学能力。因此,整个课程的主要参与者是固体中的电子。学生有望学习:1)何时或在什么条件下,量子效应在设备中变得不可忽略;2)如何计算在人工势结构中移动的电子的量子态(波函数)和能量;3)什么决定了量子固态设备的电学和光学特性。将尽早介绍量子力学的基本数学基础,然后立即介绍量子信息和量子计算,这是量子力学最重要的新兴应用之一。我们将力求在严格的数学推导和示例问题解决之间取得良好的平衡。问题将是实际的,包括量子阱红外光电探测器、太阳能电池、量子隐形传态、布洛赫振荡、LED 的带隙工程、量子级联激光器、拓扑能带结构和范德华异质结构的能带图等现代主题。必修课文:
量子计算的数学建模
Arunabh Singh Suraj Kumar Singh 电子和通信系,电子和通信系,FET,MRIIRS,法里达巴德,121003,哈里亚纳邦,印度 FET,MRIIRS,法里达巴德,121003,哈里亚纳邦,印度 摘要 - 量子计算是一种可能彻底改变计算的有利技术。它不同于传统计算,它需要计算算法和与量子力学原理相对应的实现方法。现有计算机处理器系统的时钟频率可能在未来十年内达到约 40 GHz。到那时,一个原子可能代表一个比特,但在这种条件下的电子无法用经典物理学来描述,因此,新的计算模型将变得绝对必要。量子计算的前景可能有潜力解决经典计算面临的问题。关键词:量子计算、量子比特、布洛赫球、量子寄存器、线性光学、捕获离子、光纤、激光脉冲整形等。
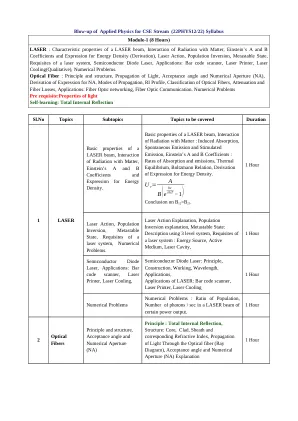
CSE 流应用物理学放大 (22PHYS12/22 ...
量子信息与量子计算原理:量子计算简介、摩尔定律及其终结、经典计算与量子计算之间的差异。量子比特的概念及其属性。布洛赫球对量子比特的表示。单量子比特和双量子比特。扩展到 N 量子比特。狄拉克表示和矩阵运算:0 和 1 状态的矩阵表示、恒等运算符 I、将 I 应用于 | 0 ⟩ 和 | 1 ⟩ 状态、泡利矩阵及其对 | 0 ⟩ 和 | 1 ⟩ 状态的运算、矩阵共轭 i) 和转置 ii) 的解释。酉矩阵 U、示例:行矩阵和列矩阵及其乘法(内积)、概率和量子叠加、规范化规则。正交性、正交性。数值问题量子门:单量子比特门:量子非门、泡利 - X、Y 和 Z 门、阿达玛门、相位门(或 S 门)、T 门多量子比特门:受控门、CNOT 门(针对 4 种不同输入状态的讨论)。交换门、受控 -Z 门、Toffoli 门的表示。
N 波段系统中的 Berry 曲率和量子度量
参数相关的哈密顿矩阵的特征值在参数空间中形成能带结构。在这样的 N 带系统中,由贝里曲率和量子度量张量组成的量子几何张量 (QGT) 通常通过数值获得的能量特征态计算得出。这里,提出了一种基于特征投影器和(广义)布洛赫矢量的 QGT 替代方法。它比特征态方法提供更多的分析见解。具体而言,仅使用哈密顿矩阵和相应的能带能量,即可获得每个能带的完整 QGT,而无需计算特征态。最显著的是,众所周知的以哈密顿矢量表示的贝里曲率双带公式被推广到任意 N 。使用三带和四带多重费米子模型说明了该形式化,尽管具有相同的能带结构,但它们具有非常不同的几何和拓扑性质。从更广泛的角度来看,这项工作中采用的方法可以用于计算任何物理量或研究任何可观测量的量子动力学,而无需明确构建能量本征态。
商业中的量子计算和区块链
五枚硬币之谜 23 纠缠——鬼魅般的超距作用 25 布洛赫球 26 肖尔算法 28 格罗弗算法 30 量子退火 32 量子隧穿 33 旅行商 34 退相干 36 量子纠错 37 结论 38 参考文献 39 第三章:数据经济 41 互联网 42 ARPANET 42 TCP/IP 43 繁荣、萧条与繁荣 44 社交媒体 45 大数据 48 结构化数据处理 49 非结构化数据处理 49 大数据架构 51 云 53 人工智能 55 人工智能的起源 55 模仿游戏 57 人工智能的化身 57 区块链 60 去中心化 60 不变性 61 可追溯性 62 量子计算 63 结论 63 参考文献 64 第四章:对金融服务的影响 65量子计算应用 66 市场风险 67 信用风险 69 技术限制 70 量子启发数字退火 71
量子信息论中泡利幺正算子的数学性质和特征
摘要-本研究探讨了泡利幺正算子的数学性质和特征及其在量子信息论中的应用。泡利算子是量子力学中的基本对象,在描述和操纵量子态方面起着至关重要的作用。通过全面的分析,我们研究了泡利算子的幺正性、厄米性、特征值性质和代数结构。我们探索了它们在布洛赫球面上的几何解释,并讨论了泡利分解定理等高级性质及其在稳定器形式中的作用。该研究表明了泡利算子在量子信息各个方面的广泛影响,包括量子门、测量、纠错码和算法。我们的研究结果强调了泡利算子在量子电路设计、纠错方案和量子技术发展中的不可或缺性。我们还确定了需要进一步研究的领域,例如泡利算子在高维系统中的行为及其在特定噪声模型的量子误差校正中的最佳用途。这项研究有助于更深入地了解这些基本的量子信息工具及其在量子计算和通信中的广泛应用。索引术语 - 数学性质、泡利幺正算子、量子信息论
绝缘范德华铁磁体中的拓扑自旋纹理
鉴于拓扑自旋纹理在信息存储技术中的潜在应用,其生成和控制是现代自旋电子学最令人兴奋的挑战之一。特别令人感兴趣的是磁绝缘体,由于其低阻尼、无焦耳加热和减少的耗散,可以提供节能的自旋纹理平台。本文证明了样品厚度、外部磁场和光激发之间的相互作用可以产生大量的自旋纹理,以及它们在绝缘 CrBr 3 范德华 (vdW) 铁磁体中的共存。使用高分辨率磁力显微镜和大规模微磁模拟方法,证明了 T-B 相图中存在一个大区域,其中存在不同的条纹畴、skyrmion 晶体和磁畴,并且可以通过相位切换机制进行内在选择或相互转换。洛伦兹透射电子显微镜揭示了磁性纹理的混合手性,在给定条件下属于布洛赫类型,但可以通过厚度工程进一步操纵为尼尔类型或混合类型。可以通过标准光致发光光学探针进一步检查不同磁性物体之间的拓扑相变,该探针通过圆偏振分辨,表明存在激子-skyrmion耦合机制。研究结果表明,vdW磁绝缘体是一种有前途的材料框架,可用于操纵和生成与原子级设备集成相关的高度有序的skyrmion晶格。
适合每个人的量子计算 PDF
量子原理允许量子比特以叠加态存在。这意味着量子比特可以处于 0、1 或这些状态的任何量子叠加态。想象一个球体,其北极和南极代表经典状态 0 和 1。球体表面上的任何一点都代表量子比特的一种可能状态。这被称为布洛赫球体表示,Bernhardt 使用该模型帮助读者直观地了解量子比特状态的抽象概念。量子比特的强大之处在于它们能够比经典量子比特容纳更多信息。要理解这一点,请考虑使用位作为最小数据单位的经典计算机。八位或一个字节可以表示 0 到 255 之间的任何数字。但是,由于叠加,八个量子比特可以同时表示 0 到 255 之间的所有数字。这不仅意味着处理能力略有提升,还意味着指数级飞跃。每增加一个量子比特,计算空间就会翻倍,从而产生传统计算无法比拟的增长曲线。Bernhardt 通过量子搜索算法的例子说明了量子比特的威力。想象一下在电话簿中搜索特定名称。在传统计算场景中,这类似于逐页翻阅,直到找到您要查找的名称——这是一个连续且耗时的过程。现在,设想一下,电话簿中的每一页