XiaoMi-AI文件搜索系统
World File Search System使用拉曼光谱法
本文在过去五十年中通过拉曼光谱法对石墨烯中缺陷计量的演变提供了历史记录。将拉曼散射应用于石墨材料中疾病水平的研究可以追溯到1970年代,并且在该领域发生了很大的进步,尤其是在2006年分离石墨烯之后。文章开始介绍与结构缺陷有关的物理学,破坏了晶体固体中的翻译对称性,引入了拉曼光谱中的选择规则的放松,该规则表现为被障碍引起的峰值,然后将其估计为重要的里程碑,并提供了主要现有协议的实际摘要。此外,我们探讨了尖端增强的拉曼光谱法对石墨烯材料中缺陷的基本方面的更深入了解,这是由于其具有高空间分辨率的光谱测量的能力。总而言之,我们概述了这种创新技术进一步利用这种创新技术的前景,以增强石墨烯缺陷的科学和计量及其在其他二维系统中的应用。
clearscope:用于亚细胞分辨率成像的完全集成的光片theta显微镜,没有横向大小约束Matthew G. Fay 1,
1 MBF Bioscience, Williston, VT 05495, USA 2 Department of Biomedical Engineering, Columbia University, New York, NY 10027, USA 3 Department of Biological Sciences, Columbia University, New York, NY 10027, USA 4 Neuroscience Institute, New York University Langone Health, New York, NY 10016, USA 5 Department of Neuroscience and Physiology, New York University Grossman School医学;纽约市,10016,美国6纽约大学格罗斯曼医学院精神病学系;纽约市,美国10016。7纽约大学神经科学中心,纽约,纽约10003,美国8综合癫痫中心,纽约大学格罗斯曼医学院神经病学系;纽约市,10016,美国9纽约大学格罗斯曼医学院神经外科系;纽约市,10016,美国,摘要的三维(3D)在动物模型的完整大脑以及大型人类和非人类和非人类灵长类动物大脑标本的整体化成像对于理解生理神经网络连接模式及其病理学改变的病理学改变而言至关重要。灯页显微镜已成为一种高效的成像方式,用于对大型清除样品的快速高分辨率成像。但是,光显微镜中照明和检测光学的正交布置限制了可以成像的样品的大小。最近开发的光片theta显微镜(LSTM)技术通过利用两个照明光路径的独特布置倾斜到检测光路径,同时允许检测光路相对于试样表面的垂直排列。在这里,我们报告了下一代,完全集成和用户友好的LSTM系统的开发,以在整个大型标本中均匀地均匀地下分辨率成像,而不会约束横向(XY)大小。此外,我们为图像获取,数据存储,预处理和后处理,增强和定量分析提供了无缝集成的工作流程。我们通过完整的小鼠大脑和人脑样品的高分辨率3D成像以及完整的数据分析(包括数字神经元追踪,血管重建和基于设计的立体分析)在3D中证明了系统性能。这种技术增强和用户友好的LSTM实现将在不同类型的非常大的样本中快速对分子和细胞特征的分子和细胞特征进行快速定量映射。关键字:轻度显微镜,轻纸theta显微镜,连接组学,神经科学:0009-0009-0009-2439-8045(M.F.),0009-0007-1876-4104(P.L.),0009-0006-4374-3711(D.D.),0009-0000-5928-8692(N.OC。),0009-0005-0168-9190(B.H.),0009-0004-0565-9872(J.B.1),0009-0003-7441-9496(N.R.),0009-0004-3698-1784(A.W.),0009- 0004-5284-1087(S.A.),0009-0009-8144-0115(P.A.),0000-0002-7559-0936(J.B.2),0000-0003-4350-0569(T.B.),0000-0002-0026-2006(C.G.),0000-0003-0044-4632(O.D.),0000-0002-7559-0936(J.B.),0000-0002-4229-2860(R.T.),0000-0003-4463-207X(J.G.)(Y.B.1,Jeffrey Blaisdell)。
相干态的乌尔曼相和乌尔曼-贝里对应关系
Berry相[1]通过绝热循环过程后获得的相位揭示了量子波函数的几何信息,它的概念为理解许多材料的拓扑性质奠定了基础[2–13]。Berry相理论建立在纯量子态上,例如基态符合零温统计集合极限的描述,在有限温度下,密度矩阵通过将热分布与系统所有状态相关联来描述量子系统的热性质。因此,将Berry相推广到混合量子态领域是一项重要任务。已有多种方法解决这个问题[14–21],其中Uhlmann相最近引起了广泛关注,因为它已被证明在多种一维、二维和自旋j系统中在有限温度下表现出拓扑相变[22–26]。这些系统的一个关键特征是 Uhlmann 相在临界温度下的不连续跳跃,标志着当系统在参数空间中穿过一个循环时,底层的 Uhlmann 完整性会发生变化。然而,由于数学结构和物理解释的复杂性,文献中对 Uhlmann 相的了解远少于 Berry 相。此外,只有少数模型可以获得 Uhlmann 相的解析结果 [ 22 – 30 ] 。Berry 相是纯几何的,因为它不依赖于感兴趣量子系统时间演化过程中的任何动力学效应 [ 31 ] 。因此,Berry 相理论可以用纯数学的方式构建。概括地说,密度矩阵的 Uhlmann 相是从数学角度几乎平行构建的,并且与 Berry 相具有许多共同的几何性质。我们将首先使用纤维丛语言总结 Berry 相和 Uhlmann 相,以强调它们的几何特性。接下来,我们将给出玻色子和费米子相干态的 Uhlmann 相的解析表达式,并表明当温度趋近于零时,它们的值趋近于相应的 Berry 相。这两种相干态都可用于构造量子场的路径积分 [32 – 37]。虽然单个状态中允许有任意数量的玻色子,但是泡利不相容原理将单个状态的费米子数限制为零或一。因此,在玻色子相干态中使用复数,而在费米子相干态中使用格拉斯曼数。玻色子相干态也用于量子光学中,以描述来自经典源的辐射 [38 – 41]。此外,相干态的Berry相可以在文献[ 42 – 45 ]中找到,我们在附录A中总结了结果。我们对玻色子和费米子相干态的 Uhlmann 相的精确计算结果表明,它们确实携带几何信息,正如完整概念和与 Berry 相的类比所预期的那样。我们将证明,两种情况下的 Uhlmann 相都随温度平稳下降,没有有限温度跃迁,这与先前研究中一些具有有限温度跃迁的例子形成鲜明对比 [ 22 – 30 ] 。当温度降至零度时,玻色子和费米子相干态的 Uhlmann 相接近相应的 Berry 相。我们对相干态的结果以及之前的观察结果 [ 22 , 24 , 26 ] 表明,在零温度极限下,Uhlmann 相还原为相应的 Berry 相。
多功能磁性纳米粒子在小鼠黑色素瘤模型中引发抗肿瘤免疫
A 马德里纳米科学高级研究中心 (Imdea Nanociencia),马德里 28049,西班牙 B 哈佛大学约翰·保尔森工程与应用科学学院,马萨诸塞州剑桥 02138,美国 CWAGITY BIGIDUTE FOR 波士顿,马萨诸塞州 02115,美国 D 马德里大学公主医院免疫学服务部,公主卫生研究所,马德里 28006,西班牙 E 纽约大学坦登工程学院生物医学工程系。纽约大学格罗斯曼医学院医学系,纽约大学,纽约州纽约 10010,美国 G 国家生物技术中心 Unity De Nabototecnologíada (CNB-CSIC),马德里 28049,西班牙
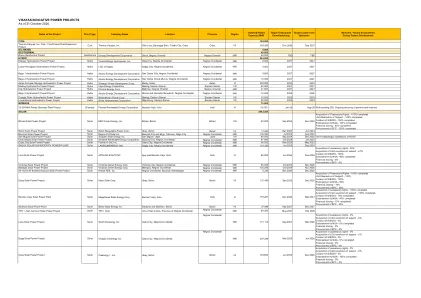
维萨亚斯指示性电力项目 截至 2024 年 10 月 31 日
获取占有权——已完成 100% 地方政府支持解决方案——已完成 100% 进行 SIS/DIS——已完成 100% 向 NGA 认可——已完成 100% 财务结算——已完成 85% EPC 采购——已完成 100% 保和太阳能公司可再生能源项目。 Ubay, Bohol Bohol VII 17.500 2023 年 12 月 2024 年 6 月 巴科洛德太阳能发电项目 Solar Negros PH Solar Inc.巴科洛德市和 Brgy。塔布南,巴戈市 西内格罗斯省 NIR 130.050 2024 年 7 月 2024 年 8 月 圣米格尔太阳能发电项目 太阳能 Sunpalo Solar Energy Inc.圣米格尔,莱特省 莱特 VIII 80.000 2024 年 9 月 2024 年 12 月 NGCP 的 138 kV Babatngon 变电站 Vista Alegre 太阳能发电项目 Solar Amatera 可再生能源公司 巴科洛德市,西内格罗斯省 西内格罗斯省 NIR 41.600 2024 年 10 月 太阳能发电项目 2025 年 1 月 您 Al Sol, Inc.加的斯市, 西内格罗斯省 西内格罗斯省 NIR 56.000 2025 年 3 月 2025 年 5 月 SAGAY SOLAR ON WATER PV POWER PLANT 太阳能 LAKESUNENERGY INC.萨盖市, 西内格罗斯省 西内格罗斯省 NIR 101.200 2026 年 6 月 2026 年 9 月
工会部长曼苏克·曼达维亚(Mansukh Mandaviya)博士通过“ FU
智能制造:CII全国智能制造与董事总经理董事长Dilip Sawhney先生印度Rockwell Automation India Ltd说:“智能制造是实现印度实现7.5万亿美元经济的目标的关键,对GDP贡献了25%,并使印度成为第二大全球制造业枢纽>有90%的领域公司是MSMES,竞争力对于创造超过1亿高技能的就业机会并将印度融入全球价值连锁店至关重要。”他强调,随着高级技术的发展,制造业,技能和高技能计划必须赋予劳动力的能力,以适应分析驱动的角色,推动经济增长和增值