XiaoMi-AI文件搜索系统
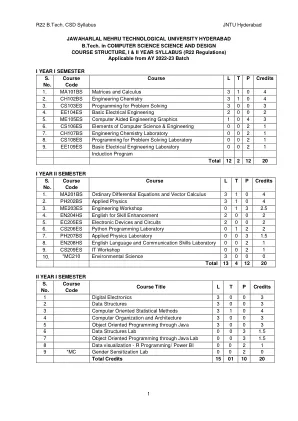
World File Search SystemR22 B.Tech. CSD 教学大纲 JNTU 海得拉巴 1 ...
写出一组线性方程的矩阵表示并分析方程组的解 查找特征值和特征向量 使用正交变换将二次形式简化为标准形式。 解决均值定理的应用。 使用 Beta 和 Gamma 函数评估不当积分 找到有/无约束的两个变量函数的极值。 评估多重积分并应用概念来寻找面积和体积 UNIT - I:矩阵 10 L 通过梯形和标准形式对矩阵进行秩,通过高斯-乔丹方法对非奇异矩阵进行逆运算,线性方程组:用高斯消元法、高斯赛德尔迭代法求解齐次和非齐次方程组。第二单元:特征值和特征向量 10 L 线性变换和正交变换:特征值、特征向量及其性质、矩阵对角化、凯莱-汉密尔顿定理(无证明)、用凯莱-汉密尔顿定理求矩阵的逆和幂、二次型和二次型的性质、用正交变换将二次型简化为标准形式。 第三单元:微积分 10 L 均值定理:罗尔定理、拉格朗日均值定理及其几何解释和应用、柯西均值定理、泰勒级数。应用定积分求曲线旋转的表面积和体积(仅限于笛卡尔坐标系)、不当积分的定义:Beta 函数和 Gamma 函数及其应用。第四单元:多元微积分(偏微分和应用)10 L 极限和连续性的定义。偏微分:欧拉定理、全导数、雅可比矩阵、函数依赖性和独立性。应用:使用拉格朗日乘数法求二元和三元函数的最大值和最小值。
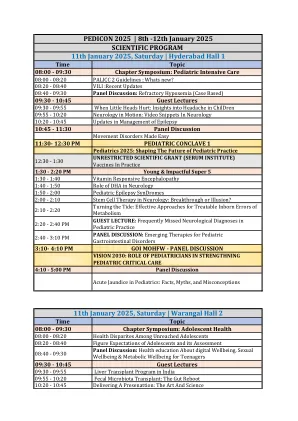
2025年1月11日,星期六|海得拉巴大厅1
Time Topic 08:00 - 09:30 Chapter Symposium: Infant & Young Child Feeding 08:00 - 08:20 New Insights into the Mastitis Spectrum 08:20 - 08:40 Colostrum: The White Gold 08:40 - 09:30 Panel Discussion: Human Milk Banking--Scopes and Horizons 09:30 - 10:45 Guest Lectures 09:30 - 09:55 Syncope Decoded 09:55 - 10:20 Approach to Pediatric hypertension 10:20 - 10:45 Rising to the Challenge: AdDressing Polio Resurgence 10:45 - 11:30 Panel Discussion Tele Echo: Bringing Cardiac Diagnostics to Your Doorstep 11:30- 12:30 PM Guest Lectures 11:30 - 12:00 Intriguing Case Scenarios In Pediatric Nephrology 12:00 - 12:30 The Fragile Filter: Preserving Kidney Function In Pediatric Patients 12:30 - 1:30 PM AWARD PAPERS 1:30 - 2:20 PM Young & Impactful Super 5 1:30 - 1:40 Echogenic Focus in Antenatal scan 1:40 - 1:50 Keeping the PDA open 1:50 - 2:00 Rhythm Rescue: Approach to SVT 2:00 - 2:10 Timing Matters: Surgical management of congenital heart disease 2:10 - 2:20风湿热复活2:20-3:10 pm来宾讲座2:20-2:45 pm心肌疾病:从心肌病到炎症2:45-3:10 pm卫生保健未来2.0 3:10-4:00
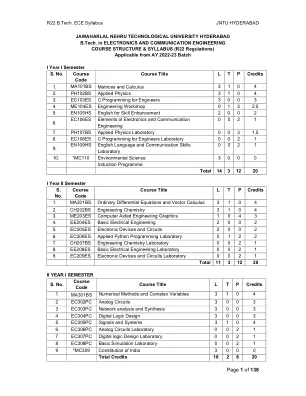
R22 B.Tech. ECE 教学大纲 JNTU 海得拉巴
写出一组线性方程的矩阵表示并分析方程组的解 寻找特征值和特征向量 利用正交变换将二次形式简化为标准形式。 解决均值定理的应用。 使用 Beta 和 Gamma 函数求不当积分 找出有/无约束的两个变量函数的极值。 评估多重积分并应用概念寻找面积、体积 UNIT-I:矩阵 10 L 通过梯形和标准形式对矩阵进行秩计算,通过高斯-乔丹方法对非奇异矩阵进行逆计算,线性方程组:通过高斯消元法、高斯赛德尔迭代法求解齐次和非齐次方程组。第二单元:特征值和特征向量 10 L 线性变换和正交变换:特征值、特征向量及其性质、矩阵对角化、凯莱-汉密尔顿定理(无证明)、利用凯莱-汉密尔顿定理求矩阵的逆和幂、二次型和二次型的性质、利用正交变换将二次型简化为标准形式。 第三单元:微积分 10 L 均值定理:罗尔定理、拉格朗日均值定理及其几何解释和应用、柯西均值定理、泰勒级数。应用定积分求曲线旋转的表面积和体积(仅在笛卡尔坐标系中)、不定积分的定义:Beta 函数和 Gamma 函数及其应用。 UNIT-IV:多元微积分(偏微分和应用)10 L 极限和连续性的定义。偏微分:欧拉定理、全导数、雅可比矩阵、函数依赖性和独立性。应用:使用拉格朗日乘数法求二元和三元函数的最大值和最小值。
第47届年度报告 - IGM图书馆 - 海得拉巴大学
名称名称联系人号E-Mail ID Librarian N Varatha Rajan (040) 23132600 NVRAJAN2002@gmail.com Director, IQAC S Srinath (040) 23132137 Iqac@uohyd.ac.in Director, CC & CNF SANJAY KUARMA SHARMA (040) 23132646 Dirccss@uohyd.ac.in Director, Tie-U GS Prasad (040) 23132119 tieu.uoh@gmail.com Director, RDC Samrat L SABAT (040) 23132800 RESAARCH@OOYD.C.in Chee Medical Officer I/C M Rajashree (040) 23132402 Helathcentre.uoh@gmail.com Chief Proctor E Harikumar (040) 23134042 cp@uohyd.in Professor I/C, CIL SRINATH (040) 23262 srinath@ohyd.ac.in Dean, Student Welfare G Nagaraju (040) 23132500 DSW-AFFICE@uohyd.ac.in Chief Warden Vineet C P Nair (040) 23132505 CWOOH@Gmail.com办公室事务总监Chetan Srivastava(040)23132808 sipuoh98@gmail.com大学工程师I/C DVN Raju(040)23132300 ue@uohyd.ac.in董事,HRDC Y Narasimhulu(040)232271 Hrdcuhar rairnem narrdc y Narasimhulu(040) (040)23132440 jatinsriiraj@yahoo.co.coin董事,距离与虚拟学习S JEELANI(04066)董事cde@uohyd.ernet.inet.inE-Mail ID Librarian N Varatha Rajan (040) 23132600 NVRAJAN2002@gmail.com Director, IQAC S Srinath (040) 23132137 Iqac@uohyd.ac.in Director, CC & CNF SANJAY KUARMA SHARMA (040) 23132646 Dirccss@uohyd.ac.in Director, Tie-U GS Prasad (040) 23132119 tieu.uoh@gmail.com Director, RDC Samrat L SABAT (040) 23132800 RESAARCH@OOYD.C.in Chee Medical Officer I/C M Rajashree (040) 23132402 Helathcentre.uoh@gmail.com Chief Proctor E Harikumar (040) 23134042 cp@uohyd.in Professor I/C, CIL SRINATH (040) 23262 srinath@ohyd.ac.in Dean, Student Welfare G Nagaraju (040) 23132500 DSW-AFFICE@uohyd.ac.in Chief Warden Vineet C P Nair (040) 23132505 CWOOH@Gmail.com办公室事务总监Chetan Srivastava(040)23132808 sipuoh98@gmail.com大学工程师I/C DVN Raju(040)23132300 ue@uohyd.ac.in董事,HRDC Y Narasimhulu(040)232271 Hrdcuhar rairnem narrdc y Narasimhulu(040) (040)23132440 jatinsriiraj@yahoo.co.coin董事,距离与虚拟学习S JEELANI(04066)董事cde@uohyd.ernet.inet.in
专用电缆 - 温州海得利电气有限公司
heatle.net › uploads 技术细节(船舶电力合作伙伴热带地区)... 不锈钢/铜/铜镍合金 1825 合金... 导体标准截面mm。24 页
野生动植物取证中的DNA技术(动物) - 海得拉巴
-Rakesh Mishra董事,CSIR -CCMB非法野生动植物贸易是全球威胁。在发展中国家,有标志性物种,例如老虎,亚洲大象,单角犀牛。定期将一些新的野生动植物物品包括在非法野生动植物贸易中。穿衣尺度,红色沙纸上,巨型盖克和监测蜥蜴正在偷猎以灭绝其身体部位。这些项目是无法识别的,并且从这种材料中涉及的物种的鉴定极具挑战性。此处概述的协议是十年来测试,标准化和成功应用基于DNA的技术在野生动植物法医学诊断中的结果。如果此SOP之后是感兴趣的各方,则可以及时解决一些野生动植物犯罪。
鸿海111年报_en(0516追加)_for_print.pdf
在过去三年中,全球Covid-19的大流行不仅威胁到人类健康,而且对全球经济产生了影响。尽管大流行的影响逐渐减弱,但各个国家通过促进大流行期间经济的货币扩张政策导致了通货膨胀。随后在2022年,全球经济进入了利率上升的周期。尽管增加利率在控制通货膨胀和稳定经济发展方面起着关键作用,但这些政策对经济前景包含一定程度的负面影响。公司运营的技术行业也受到影响。考虑到2022年的许多挑战,所有员工的努力都能够为该公司(集团)提供创纪录的高收入和15年以来每股收益最佳。
R22 B.Tech. CSE(AI 和 ML)课程大纲 JNTU 海得拉巴
写出一组线性方程的矩阵表示并分析方程组的解 查找特征值和特征向量 使用正交变换将二次形式简化为标准形式。 解决均值定理的应用。 使用 Beta 和 Gamma 函数评估不当积分 找到有/无约束的两个变量函数的极值。 评估多重积分并应用概念来寻找面积和体积 UNIT - I:矩阵 10 L 通过梯形和标准形式对矩阵进行秩,通过高斯-乔丹方法对非奇异矩阵进行逆运算,线性方程组:用高斯消元法、高斯赛德尔迭代法求解齐次和非齐次方程组。第二单元:特征值和特征向量 10 L 线性变换和正交变换:特征值、特征向量及其性质、矩阵对角化、凯莱-汉密尔顿定理(无证明)、用凯莱-汉密尔顿定理求矩阵的逆和幂、二次型和二次型的性质、用正交变换将二次型简化为标准形式。 第三单元:微积分 10 L 均值定理:罗尔定理、拉格朗日均值定理及其几何解释和应用、柯西均值定理、泰勒级数。应用定积分求曲线旋转的表面积和体积(仅限于笛卡尔坐标系)、不当积分的定义:Beta 函数和 Gamma 函数及其应用。第四单元:多元微积分(偏微分和应用)10 L 极限和连续性的定义。偏微分:欧拉定理、全导数、雅可比矩阵、函数依赖性和独立性。应用:使用拉格朗日乘数法求二元和三元函数的最大值和最小值。