机构名称:
¥ 13.0
写出一组线性方程的矩阵表示并分析方程组的解 寻找特征值和特征向量 利用正交变换将二次形式简化为标准形式。 解决均值定理的应用。 使用 Beta 和 Gamma 函数求不当积分 找出有/无约束的两个变量函数的极值。 评估多重积分并应用概念寻找面积、体积 UNIT-I:矩阵 10 L 通过梯形和标准形式对矩阵进行秩计算,通过高斯-乔丹方法对非奇异矩阵进行逆计算,线性方程组:通过高斯消元法、高斯赛德尔迭代法求解齐次和非齐次方程组。第二单元:特征值和特征向量 10 L 线性变换和正交变换:特征值、特征向量及其性质、矩阵对角化、凯莱-汉密尔顿定理(无证明)、利用凯莱-汉密尔顿定理求矩阵的逆和幂、二次型和二次型的性质、利用正交变换将二次型简化为标准形式。 第三单元:微积分 10 L 均值定理:罗尔定理、拉格朗日均值定理及其几何解释和应用、柯西均值定理、泰勒级数。应用定积分求曲线旋转的表面积和体积(仅在笛卡尔坐标系中)、不定积分的定义:Beta 函数和 Gamma 函数及其应用。 UNIT-IV:多元微积分(偏微分和应用)10 L 极限和连续性的定义。偏微分:欧拉定理、全导数、雅可比矩阵、函数依赖性和独立性。应用:使用拉格朗日乘数法求二元和三元函数的最大值和最小值。
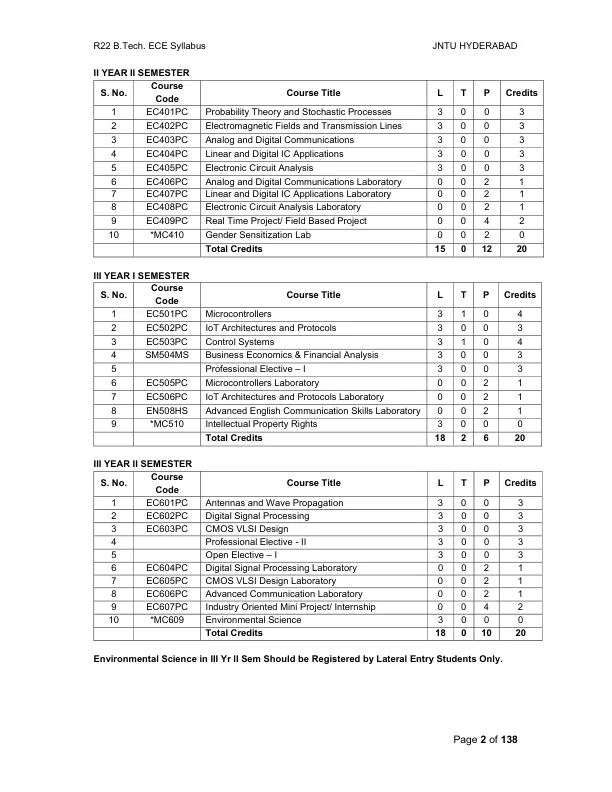
R22 B.Tech. ECE 教学大纲 JNTU 海得拉巴
主要关键词