XiaoMi-AI文件搜索系统
World File Search System替代重力公式之间的互惠关系
我们根据Bhandari最近提出的工作进行了比较牛顿的普遍重力法与校正的模拟方法,在该方法中保持了引力常数g。相对于质量中心之间的距离,两个隔离重力公式之间存在互惠关系。我们总结了两个引力公式的一对一映射。我们不需要爱因斯坦的时空弯曲结构。
物理学理学硕士 - 课程结构和教学大纲
牛顿运动定律,牛顿力学的缺点。拉格朗日力学:约束、广义坐标、虚功原理、达朗贝尔原理、保守和非保守系统的拉格朗日运动方程、达朗贝尔原理的拉格朗日方程、拉格朗日公式的应用。汉密尔顿力学:广义动量和循环坐标、汉密尔顿原理和拉格朗日方程、汉密尔顿运动方程、汉密尔顿公式的应用、鲁斯公式。中心力:两体中心力问题、轨道微分方程、开普勒定律、维里定理、中心力场中的散射、卢瑟福散射。变分原理和最小作用原理。正则变换。泊松和拉格朗日括号、刘维尔定理、相空间动力学、稳定性分析。汉密尔顿-雅可比方程和向量子力学的过渡。耦合振子。刚体动力学。非惯性坐标系。对称性、不变性和诺特定理。狭义相对论和相对论力学基础。四矢量公式。电动力学协变公式基础。
数值方法模块 14:等值插值...
此公式可以更好地估计 xn 附近点 x 处的 f 值,因为公式尽可能早地使用最接近该 x 的数据点,并且还利用了最多 n 阶后向(实际上是相除)差值。同样的推理表明,该公式可能不适合估计远离 xn 的点 x 处的 f 值,即靠近观测数据的中间或开始处。但是,正如下图和下一模块中介绍的数值实验所示,这种限制没有任何实际意义。例 1:设 f(x) = e 2x Cos 3x,其中 x Є [0, 1]。使用 5 次牛顿前向/后向差分插值多项式,在节点 x = 0、x = 0.2、x = 0.4、x = 0.6、x = 0.8 和 x = 1 上找到 f(0.1)、f(0.5) 和 f(0.9) 的近似值。给定 6 个节点和相应的函数值,计算表 2 中给出的前向/后向差分。然后根据牛顿前向/后向差分插值公式,计算 f(0.1)、f(0.5)、f(0.9) 的值并将其与实际值进行比较。
中级大学物理学 - 理查德·菲茨帕特里克(Richard Fitzpatrick)
1牛顿动力学5 1.1单元。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。5 1.1.1 MKS单位。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。5 1.1.2标准预固定。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。6 1.1.3其他单元。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。7 1.1.4维度分析。。。。。。。。。。。。。。。。。。。。。。。。。。。8 1.1.5得出物理关系。。。。。。。。。。。。。。。。。。。。。。8 1.1.6缩放定律。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。9 1.2牛顿运动定律。。。。。。。。。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>10 1.2.1简介。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>10 1.2.2牛顿的第一项运动定律。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>10 1.2.3牛顿第二条运动定律。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>11 1.2,4纽约的第三运动定律。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>12 1.3单个粒子的运动。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>13 1.3.1冲动。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>13 1.3.2工作。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>。 div>14 1.3.3保守力量。 div>。 div>。 div>。 div>。。。。。。。。。。。。。。。。。。。。。。。。15 1.3.4势能。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。16 1.3.5节能。。。。。。。。。。。。。。。。。。。。。。。。。。。。17 1.3.6能量图。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。17 1.4许多颗粒系统的运动。。。。。。。。。。。。。。。。。。。。。20 1.4.1运动方程。。。。。。。。。。。。。。。。。。。。。。。。。。。。20 1.4.2质量中心。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。21
AQA GCSE三部曲科学:如何成功!
•标量和矢量数量,接触和非接触力,重力,导致力,工作和能量传递,力和弹性,距离和位移,速度和位移,速度,速度,距离,距离时间图,加速度,牛顿的第一,第二和第三法律,力量,力量和制动 - 影响停止距离的距离,和反应时间和反应时间,较高的动量,仅(更高)(较高)(较高)(较高)(仅)6。波;
机电一体化工程 - 入学先决条件
颗粒和刚体的物理学运动学(位置,线性和旋转运动中的速度和加速度);颗粒和刚体的动力学(力和力矩,牛顿运动定律);刚体的平衡;拉格朗日方程;节能原则(工作,能源和权力);热力学;热运输(传导,对流,辐射);电磁学(Coloumb的法律,生物 - 萨瓦特法律,高斯法律,麦克斯韦法律)。
Flaminia Giacomini 博士
在量子理论的界面上理解引力的基本性质是理论物理学中一个重要的未决问题。最近,对引力量子系统的研究,例如在位置的量子叠加中准备的、以引力场为源的大规模量子系统,引起了广泛关注:量子光学实验正在努力在实验室中实现这种场景,测量与量子源相关的引力场有望提供一些有关引力性质的信息。在理论方面,量子信息工具用于解释结果。然而,关于这些实验可以得出关于引力量子性质的确切结论,仍然存在悬而未决的问题,例如,这种状态下的实验是否能够测试引力场的更多部分。在我的演讲中,我将介绍一个新的结果,其中非局域量子源产生的效应无法使用牛顿势再现,也无法作为经典广义相对论的极限。这些效应原则上可以通过进行干涉实验来测量,并且与引力子发射无关。确定比牛顿势能可再现的更强的引力量子方面,对于证明引力场的非经典性和规划新一代实验(在比迄今为止提出的更广泛的意义上测试引力的量子方面)至关重要。
研究方法的范式
流动微生物的密度在减轻和监测动量,热和溶质边界层时表现出动态特征。看到这一点,我们检查了卡森纳米流体悬浮液的流动特征,这是由于片张的拉伸而引起的。研究了辐射,不均匀的散热器或源,热经液和布朗运动的影响。流是层流和时间依赖的。检查热量和传质特征的关节影响。速度滑移边界条件被认为是研究流量特征。建模的方程式是高度耦合和非线性的。因此,对于此模型是不可能的分析解决方案。因此,我们提出了一个数值解决方案。合适的相似性被思考将原始PDE的变态变成ODE,然后通过利用基于Runge-Kutta的射击技术来解决。借助图详细讨论了各种参数在流场上的影响。同时阐明牛顿和非牛顿液。被描述,嗜热参数的增强导致热量增强,从而降低了浓度。此外,特征是生物对流刘易斯的数量和小伙子的数量降低了动感微生物的密度。关键字:MHD,热量和传质,生物概念,卡森流体,布朗运动。
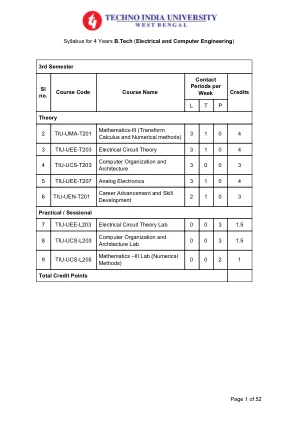
4 年制 B.Tech(电气和计算机)课程大纲...
详细课程大纲 第一单元:变换微积分拉普拉斯变换:拉普拉斯变换、性质、逆、卷积、用拉普拉斯变换求某些特殊积分、初值问题的解。傅里叶级数:周期函数、函数的傅里叶级数表示、半程级数、正弦和余弦级数、傅里叶积分公式、帕塞瓦尔恒等式。傅里叶变换:傅里叶变换、傅里叶正弦和余弦变换。线性、缩放、频移和时移性质。傅里叶变换的自互易性、卷积定理。应用于边界值问题。第二单元:数值方法近似和舍入误差、截断误差和泰勒级数。插值 - 牛顿前向、后向、拉格朗日除差。数值积分 - 梯形、辛普森 1/3。通过二分法、迭代法、牛顿-拉夫森法、雷古拉-法尔西法确定多项式和超越方程的根。通过高斯消元法和高斯-西德尔迭代法求解线性联立线性代数方程。曲线拟合-线性和非线性回归分析。通过欧拉法、修正欧拉法、龙格-库塔法和预测-校正法求解初值问题。
Venglustat,一种口服的葡萄糖基酰胺
一个溶酶体疾病单位,艾登布鲁克医院,剑桥大学医院中心兼儿科大学辛辛那提大学医学院,俄亥俄州俄亥俄州俄亥俄州俄亥俄州E国家E国家血液学医学研究中心,莫斯科,俄罗斯f儿科,营养和代谢疾病系,儿童纪念健康研究所,波兰G sanoide comfornity c Comprister,Qurand comfine comcan i comfor阿姆斯特丹,荷兰J,以前是美国马萨诸塞州剑桥的萨诺夫;目前,美国马萨诸塞州沃特敦的Eloxx Pharmaceuticals,马萨诸塞州沃特敦,前美国马萨诸塞州弗雷明汉。目前,目前,美国马萨诸塞州牛顿的贝丝·瑟伯格·孤儿(Beth Thurberg Orphan Science LLC) FilièreG2M,Metabern网络,凡尔赛大学医学遗传学系目前,美国马萨诸塞州牛顿的贝丝·瑟伯格·孤儿(Beth Thurberg Orphan Science LLC) FilièreG2M,Metabern网络,凡尔赛大学医学遗传学系