机构名称:
¥ 1.0
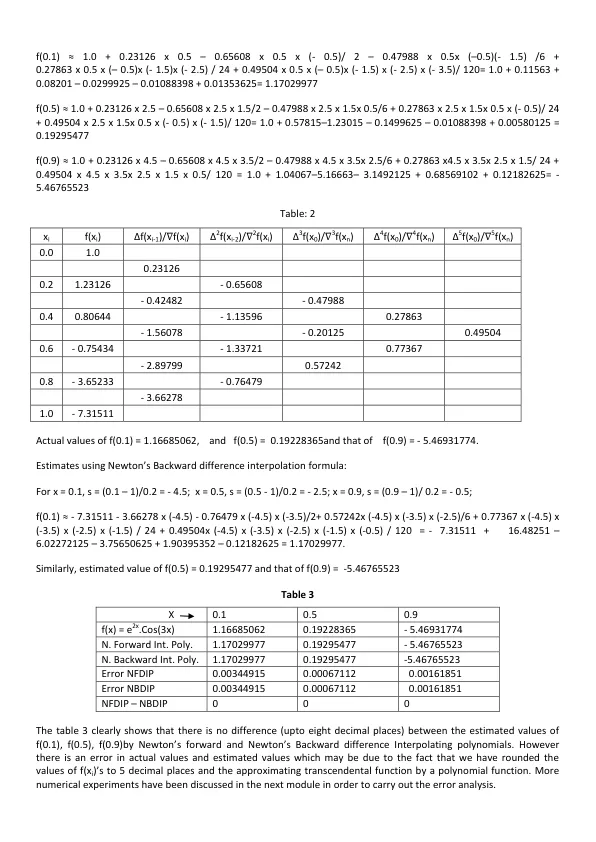
此公式可以更好地估计 xn 附近点 x 处的 f 值,因为公式尽可能早地使用最接近该 x 的数据点,并且还利用了最多 n 阶后向(实际上是相除)差值。同样的推理表明,该公式可能不适合估计远离 xn 的点 x 处的 f 值,即靠近观测数据的中间或开始处。但是,正如下图和下一模块中介绍的数值实验所示,这种限制没有任何实际意义。例 1:设 f(x) = e 2x Cos 3x,其中 x Є [0, 1]。使用 5 次牛顿前向/后向差分插值多项式,在节点 x = 0、x = 0.2、x = 0.4、x = 0.6、x = 0.8 和 x = 1 上找到 f(0.1)、f(0.5) 和 f(0.9) 的近似值。给定 6 个节点和相应的函数值,计算表 2 中给出的前向/后向差分。然后根据牛顿前向/后向差分插值公式,计算 f(0.1)、f(0.5)、f(0.9) 的值并将其与实际值进行比较。
数值方法模块 14:等值插值...
主要关键词