XiaoMi-AI文件搜索系统
World File Search System对可再生能源进行简要评估,以确定发展中国家偏远岛屿 100% 可再生能源微电网的最佳规模:以孟加拉国为例
摘要:本研究探讨了孟加拉国目前的能源状况、可再生能源 (RE) 的可能性,并为孟加拉国圣马丁岛设计了一个最佳的 100% 基于可再生能源的离网电力系统。提出了基于光伏 (PV) 电池、电池储能系统 (BESS)、燃料电池 (FC) 和电解厂 (EP) 的混合可再生微电网的最佳规模。先进的直接负荷控制 (ADLC) 和屋顶光伏以最低成本满足能源需求,并通过销售海水电解生产的化学产品实现利润最大化。使用 MATLAB ® 软件,利用混合整数线性规划 (MILP) 优化技术探索了四种情况,以证明所建议电力系统的有效性。案例 1 中的系统成本低于其他情况,但没有盈利的机会。案例 2、3 和 4 的安装成本较大,分别可在 8.17、7.72 和 8.01 年内通过利润偿还。虽然案例 3 的收入比案例 2 高 6.23%,比案例 4 高 3.85%,但案例 4 被认为是最可靠的电力系统,因为它可以以最低的成本满足能源需求,同时增加利润,不会给客户带来负担。
配电网规划中基于事件的储能、电压调节器和基础设施升级分配
摘要 — 本文介绍了一种新颖的数值方法,旨在寻找一种可防止未来拥塞和电压问题的配电网扩建计划。预测的热和电压违规事件的持续时间和强度用于确定基础设施(即线路/电缆)升级、电压调节器和储能系统安装的潜在候选池。该方法还补充了一种算法,用于获得这些候选者的最低成本列表,该算法使用二进制线性规划解决所有约束违规事件。通过大量高分辨率准静态时间序列模拟,使用改进的 IEEE 33 总线网络和爱尔兰西部的真实 1171 总线馈线验证了该方法。考虑了三个候选池和三个成本预测,以探索该方法对不同场景的敏感性。结果表明,所提出的方法是设计师、规划人员和政策制定者的多功能工具。该方法可以确保投资计划解决所有预测的违规事件。尽管如此,我们表明接受边际违规程度是可以接受的,并且可以大大降低投资成本。
布鲁塞尔自由大学 AI 工具箱 Bargiacchi, Eugenio
存在几个与 AI-Toolbox 功能部分重叠的库。MADP(Oliehoek 等人,2017)是最著名的工具箱之一。它用 C++ 编写,面向多智能体部分可观察模型,并提供多种算法。MADP 是面向对象的,因此类的层次结构很大,而 AI-Toolbox 的设计更紧凑。此外,MADP 没有 Python 绑定。BURLAP 是一个用于强化学习和规划的广泛的 JAVA 库。它包含可视化环境的代码,可与 ROS 框架一起使用(Quigley 等人,2009)。它主要关注完全可观察的环境,而 AI-Toolbox 包含多种最先进的 POMDP 算法。pomdp-solve 是 Anthony Cassandra 编写的 C 库,其中包含相对较旧的 POMDP 算法(最新的算法发表于 2004 年)。它还需要商业许可的 CPLEX 线性规划求解器。MDPToolbox(Chades 等人,2014 年)是用于单代理 MDP 算法的 MATLAB 工具箱。相比之下,AI-Toolbox 还支持 bandits、POMDP 和 MMDP 算法。还有其他工具箱,例如 PyMDPToolbox、JuliaPOMDP(Egorov 等人,2017 年)、ZMDP 和 APPL,但它们的范围比 AI-Toolbox 小得多。
区域能源系统的最新进展:综述
术语 缩写 AC 吸收式制冷机 ATES 蓄水层热能储存 BDHC 双向区域供热制冷 BTES 钻孔热能储存 CC 压缩式制冷机 CCCP 传统中央循环泵 CCHP 冷热电联产 CHP 热电联产 COP 性能系数 DC 区域制冷 DH 区域供热 DHC 区域供热制冷 DHW 生活热水 DS 区域系统 DVSP 分布式变速泵 EA 电力调节 EAC 电力调节能力 EC 电动制冷机 EES 工程方程求解器 ESS 储能系统 GSHP 地源热泵 GT 燃气轮机 HEX 热交换器 HP 热泵 HRSG 热回收蒸汽发生器 ICE 内燃机 LTDHC 低温区域供热制冷 MILP 混合整数线性规划 MINLP 混合整数非线性规划 NG 天然气 PGU 发电机组 PHE 板式换热器 PSO 粒子群优化 PV 光伏 RES 可再生能源 SNG 合成天然气 TES 热能储存 TEST 热能储存罐
电力系统中边际瓶颈识别...
为了量化对应于给定调度策略 p * 的电力系统能力,[2] 提出了可调度区域 (DPR) 的概念,该概念似乎既有效又鼓舞人心。另一方面,一个有趣的问题是哪个约束最有可能被违反。这个主题还没有得到广泛的研究,[3] 报告了开创性的工作,其提出通过将 p * 投影到 DPR 的每个边界来确定这个约束。到 p * 距离最近的边界将是最危险的瓶颈。然而,WPPE 的相关性是预测 WPG 的固有性质,却被忽略了。为了弥补这一空白,本文提出了一种在考虑 WPPE 相关性的情况下识别电力系统边际瓶颈的方法,从而对本研究课题进行有益的补充,并为电力系统运营商提供有用的信息。该方法基于用椭圆凸集表示风力发电区域 (WGR) 的公式化,该区域描述了实现的风力发电区域可能落入的空间。然后将识别过程公式化为三级最大-最大-最小问题。利用所提出的方法生成适当的初始点,可以通过基于迭代线性规划 (ITLP) 的算法来解决该问题。在两个测试系统上的仿真表明
工艺灵活性和不完美预测对哈伯-博世绿色氨操作和设计的影响
本文采用两种方法来评估灵活性在绿色氨工厂中的作用:用于工厂设计的线性规划 (LP) 和用于工厂运行的模型预测控制 (MPC)。前一种方法已用于其他绿色氨生产分析,11 – 15 尽管本文提出了一种修改方法来确定存储单元的循环对氨价格的影响程度,并给出了新的灵敏度结果。后一种 MPC 方法在孤岛绿色氨工厂中的应用是新颖的,并且为 LP 提供的结果设置了保护栏。MPC 的目的不是设计专门确定氨工厂运行参数(温度、压力、进料比等)的控制回路;相反,MPC 的目的是作为一种确定氨工厂设定点的算法。换句话说,这里介绍的 MPC 类似于级联控制布置中的主回路,决定电力分配和氨产量。对于这两个模型,天气数据均来自 ERA5,并使用标准涡轮机曲线 13 和 Python 上的 PVLib 模块转换为风能和太阳能数据。16
论文标题(使用样式
摘要 — 预计大型储能设施 (ESF) 将成为未来能源市场的重要组成部分,以增加可再生能源的渗透率。本文开发了一种新的优化算法,以参与大型商业 ESF 应对可再生能源波动。ESF 是一家投资者所有并独立运营的公司,力求最大化其总利润,同时对冲系统净负荷变化。为此,设想了一种精确计算高效的双层混合整数线性规划 (MILP)。ESF 运营商试图在较高级别最大化自己的利润,而 ISO 则寻求在较低级别出清市场。原则上,ESF 将能够构建其竞价/报价曲线以从不同市场购买/出售。为了保持问题的可处理性,每个较低级别都被其 KKT 最优条件取代,并使用强对偶理论将非线性转换为线性等价物,从而呈现单级 MILP,并因此重铸为 MPEC。此外,根据信息差距决策理论(IGDT)工具构建了所提出的框架,以捕捉不确定性对 ESF 利润的不利影响。
多准则决策分析平台及应用
本文全面介绍了 REACT-DECARB 能源规划平台,该平台旨在协助评估岛屿电网的脱碳情景,并应用于八 (8) 个欧盟岛屿。这些情景是在“地平线 2020”欧盟项目的背景下开发的,该项目采用了可再生能源生产预测和优化混合整数线性规划模型。该平台采用能源和经济模块、生命周期评估和多标准决策分析来促进情景的综合评估,并使决策者能够充分掌握能源系统脱碳的技术、环境、经济和社会方面。结果表明,应谨慎考虑岛屿电力自治,并且只有在不优先考虑成本标准的情况下才是一种有效的选择。此外,还确定在电力生产碳成本低的国家寻求自治可能不利于环境。已经进行了多次岛屿间比较,结果表明 REACT-DECARB 平台可以帮助规划人员和决策者确定最佳可用方案,根据标准权重定义敏感性问题,并与当地社区达成共识,从而制定岛屿向脱碳能源未来转型的路线图。
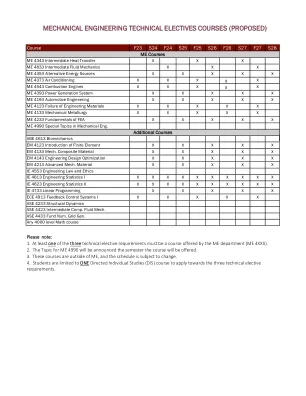
机械工程技术选修课程(拟议)
为了帮助我们的学生选择这些课程,我们还建议在目前的技术选修课列表中扩充一个按学科/兴趣分组的课程列表。下面是分组示例。突出显示的课程目前未列在机械工程技术选修课列表中,但我们希望考虑它们。下面的课程列表已经过审查,以确保我们的学生满足这些课程的先决条件要求。能源/环境 ME 4353 – 替代能源 ME 4373 – 空调 ME 4990 – 发电系统 PTE 4993 - 石油经济分析 ME 4543 – 内燃机材料 ME 4123 – 工程材料故障 ME 4133 – 机械冶金学 ABE 4523 - 生物医学材料 CHE 4143 - 高级聚合物/复合材料 EM 4133 – 复合材料力学流体/热力学 ME 4833 – 国际。流体力学 ASE 4423 – 国际计算机流体动力学 ME 4343 – 中级传热 ME 4543 – 内燃机 数学和科学 IE 4613 - 工程统计学 I IE 4624 - 工程统计学 II IE 4733 – 线性规划 ASE 4233 - 结构动力学 任何 4000 级数学课程
基于 MILP 的混合微电网统计优化设计
摘要-最近由于技术、经济和环境原因,可再生能源在电力系统中的渗透率有所提高。另一方面,在偏远地区和有能力的地区利用这些资源作为孤立的微电网有几个优点。本文研究了一种混合微电网,包括光伏 (PV)/风能/储能。它位于伊朗哈尔哈勒。本研究的目的是实现最佳能源管理和微电网规模。由于收获的可再生能源的数量与季节和气候问题密切相关,因此基于它们的具体值来规划系统是一种过于简单的做法。因此,除了环境和运营等传统约束外,还考虑了现场风速的估计。采用蒙特卡罗方法来建模和估计风行为。此外,为了调节微电网的生产和需求,实施了需求响应 (DR) 计划,以提高可再生能源的贡献。规划被构建为一个优化问题。它被表述为混合整数线性规划 (MILP)。通过求解该问题,可以确定能源的规模和生产量以及存储条件。最后,使用 GAMS 对两种情景的所有季节进行了所提出的方法模拟。结果表明,所研究电网的能源管理和成本降低效果理想。