XiaoMi-AI文件搜索系统
World File Search System执行委员会的议程
cas,JanHrubý继续开发一种适用于当代Helmholtz Energy模型的新混合模型,这与病毒系数的严格混合规则一致。发布的结果[3]包括模型的一般表述,病毒膨胀高达4度,并发现该模型的简单变体在使用范德华混合规则的标准方法时,将模型的简单变体应用于状态的两个参数立方方程。进一步的工作(在博尔德的第18个ICPW上进行报告)包括对简单流体混合物的热力学特性和相位平衡的预测计算,事实证明这是成功的。然而,事实证明,对蒸气液相平衡(VLE)和状态近距离进行建模要求状态方程在饱和蒸气和饱和液态密度之间显示单个范德华环。包括IAPWS-95在内的当前状态多轴方程显示了多个范德华循环。因此,似乎非常希望普通水的特性的未来基本表述显示出单个范德华循环,并且在亚稳态蒸气和液体区域中的实验数据和分子模拟都尽可能支持。
超快相干 THz 晶格动力学与范德华反铁磁体 FePS 3中的自旋耦合
少原子层薄材料 [1–3] 的合成引发了大规模研究的火花,旨在操控其宏观特性。最近,二维磁有序材料也已生成。[4–7] 这些化合物的长程磁序似乎极易受到晶格畸变的影响,这是因为磁各向异性在稳定二维磁体中的长程有序方面发挥了作用。[8] 通过各种机制超快产生声子已被证明是在基本时间尺度上驱动和控制块体磁体自旋动力学的有力工具。[9–14] 这种途径也适用于范德华二维材料晶体,最近在铁磁 CrI 3 晶体中发现动态自旋晶格耦合就证明了这一点。 [15] 从自旋电子学角度来看,二维反铁磁体与铁磁体相比具有几个基本优势。主要优势在于基态更稳定,磁共振频率在 THz 范围内,比铁磁体高几个数量级。至关重要的是,反铁磁磁子与声子的耦合处于光学声子的能量范围内,这导致了最近有关二维反铁磁材料中杂化磁子-声子准粒子的报道。[16–20] 因此,光驱动的集体晶格模式具有在二维反铁磁体中光学控制长程磁序的潜力,这是基于已证实的可能性,即使光子能量远离其本征频率,也可以完全相干地驱动此类模式[21,22],也基于它们与磁子的强耦合。在此背景下,过渡金属三硫属磷酸盐(MPX3,其中M = Ni、Fe、Mn、... 和X = S、Se)代表了一类有趣的范德华反铁磁体。[23–26] 虽然据报道在独立的 NiPS3 块体单晶中 [27] 可以产生光学磁振子,但这种材料缺乏可扩展性到二维极限。事实上,实验证明,NiPS3 的单原子层在磁排序上与 MnPS3 [28] 和 FePS3 [25] 并无不同。
超快相干 THz 晶格动力学与范德华反铁磁体 FePS3 中的自旋耦合
少原子层薄材料 [1–3] 的合成引发了大规模研究的火花,旨在操控其宏观特性。最近,二维磁有序材料也已生成。[4–7] 这些化合物的长程磁序似乎极易受到晶格畸变的影响,这是因为磁各向异性在稳定二维磁体中的长程有序方面发挥了作用。[8] 通过各种机制超快产生声子已被证明是在基本时间尺度上驱动和控制块体磁体自旋动力学的有力工具。[9–14] 这种途径也适用于范德华二维材料晶体,最近在铁磁 CrI 3 晶体中发现动态自旋晶格耦合就证明了这一点。 [15] 从自旋电子学角度来看,二维反铁磁体与铁磁体相比具有几个基本优势。主要优势在于基态更稳定,磁共振频率在 THz 范围内,比铁磁体高几个数量级。至关重要的是,反铁磁磁子与声子的耦合处于光学声子的能量范围内,这导致了最近有关二维反铁磁材料中杂化磁子-声子准粒子的报道。[16–20] 因此,光驱动的集体晶格模式具有在二维反铁磁体中光学控制长程磁序的潜力,这是基于已证实的可能性,即使光子能量远离其本征频率,也可以完全相干地驱动此类模式[21,22],也基于它们与磁子的强耦合。在此背景下,过渡金属三硫属磷酸盐(MPX3,其中M = Ni、Fe、Mn、... 和X = S、Se)代表了一类有趣的范德华反铁磁体。[23–26] 虽然据报道在独立的 NiPS3 块体单晶中 [27] 可以产生光学磁振子,但这种材料缺乏可扩展性到二维极限。事实上,实验证明,NiPS3 的单原子层在磁排序上与 MnPS3 [28] 和 FePS3 [25] 并无不同。
劳伦斯·伯克利国家实验室
缩小尺寸中的磁性材料不仅是磁性基础研究的出色平台,而且在技术进步中起着至关重要的作用。单层2D范德华系统中固有磁性的发现引起了巨大的兴趣,但是1D磁性范德华材料的单链极限在很大程度上尚未开发。本文报告了具有组成MX 3(M = Cr,V和X = Cl,Br,I)的1D磁范德华材料的家族,并在碳纳米管保护性核心内以完全分离的方式制备。原子分辨率扫描透射电子显微镜确定了独特的结构,这些结构与众所周知的2D蜂窝晶状体MX 3结构相差。密度功能理论计算揭示了电荷驱动的可逆磁相变类。
编目 MoSi2N4 和 WSi2N4 范德华异质结构:用于激子太阳能电池应用的卓越材料平台
太阳能转化为电能是一种很有前途的清洁能源,可为未来更可持续的技术格局提供动力。尽管传统硅基太阳能电池得到了广泛应用,但不断提高太阳能转化为电能的转换效率仍然是一项艰巨的挑战。传统晶体硅 pn 结太阳能电池受到光生电子空穴对非辐射复合的困扰 [1],这严重限制了其太阳能转化为电能的效率。[2] 硅太阳能电池还需要使用更厚的层来实现更长的光路,从而获得更好的光吸收,这从根本上限制了它们在超紧凑和低质量太阳能电池设计中的应用。[3] 寻找超越传统硅 pn 结太阳能电池的新型纳米材料和器件结构仍然是一个悬而未决的研究挑战,迫切需要解决。
科学家实现通用技术 - 称为范德华挤压 - 用于2D金属的原子制造
VDW砧座由两个单一晶体MOS 2单层在蓝宝石上生长。砧座对于生产2D金属至关重要,原因有两个。首先,单层MOS 2 /SAPPHIRE的原子平坦,无骨的表面确保大规模均匀的2D金属厚度。第二,蓝宝石和单层MOS 2(> 300 GPA)的高年轻人的模量使它们能够承受极端的压力,从而使两个砧之间形成2D金属到
范德华(Van der Waals)的应变工程的最新进展2D材料:可调电气,电化学,磁性和光学特性
对应物。[2]因此,2D材料非常适合柔性光电子,并且有可能用于下一代超薄电子和光电设备。[1]在2004年发现石墨烯时,首先实现了2D材料的概念。[4]石墨烯对其出色的电气,光学和机械性能引起了广泛的关注。[4-6]已经研究了各种技术应用,包括Spintronics,sensors,opetelectronics,SuperCapitors和Solar Cells等。[5,7] Besides graphene, other 2D materials, such as h-BN, phosphorene, silicene, germanene, and transition metal dichalcogenides (molybdenum disulfide (MoS 2 ), molybdenum diselenide (MoSe 2 ), tungsten disulfide (WS 2 ), and tungsten diselenide (WSe 2 ), etc.),近年来已经进行了广泛的研究。[1,8–11]单层二维材料的厚度通常在订单上或小于1 nm。同时,它们的侧向尺寸可以达到更大的尺寸(从微米到偶数英寸),并且在随后的处理或进行特征或设备应用程序的后续处理或后续测量之前,可以将2D材料转移到不同的基板上。
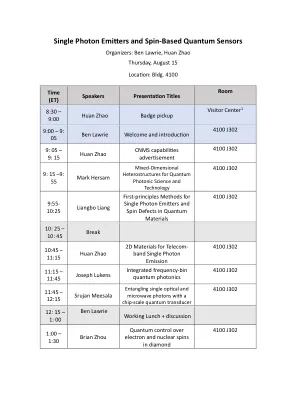
单光子发射器和基于自旋的量子传感器
层状二维 (2D) 材料主要通过范德华键相互作用,这为不受外延晶格匹配要求约束的异质结构创造了新的机会 [1]。然而,由于任何钝化的、无悬空键的表面都会通过非共价力与另一个表面相互作用,因此范德华异质结构并不仅限于二维材料。具体来说,二维材料可以与多种其他材料(包括不同维度的材料)集成,形成混合维度范德华异质结构 [2]。此外,化学功能化为调整二维材料的性质和异质界面间的耦合程度提供了更多机会 [3]。在本次演讲中,我们将探讨混合维度异质结构在量子光子科学和技术中的前景,特别关注化学功能化如何操纵和增强应变二维过渡金属二硫属化物中的单光子发射 [4]。除了技术含义之外,本次演讲还将探讨几个基本问题,包括能带排列、掺杂、陷阱态以及跨混合维异质界面的电荷/能量转移。
EDGE 文章 - RSC 出版
通过稳定的原子级精确表面实现二维电子态的实现,进一步激发了人们对低维固体的研究,这种固体可以承载接近单链状态的高度受限的一维状态。在目前建立的二维范德华晶体中,一维电子态或光学态通常通过带有底层一维基序的二维晶格(如磷烯)获得,8,9 或者通过自下而上的路线,通过基底和生长工程破坏平面内共价键的形成,10,11 催化 VLS 生长,12-14 人工台阶边缘,15 或在碳纳米管内部生长,从而引导过渡金属二硫属化物晶格生长成其一维对应物。 16 由于其结构类似于二维范德华晶体,由亚纳米厚的一维或准一维(q-1D,指具有非各向同性横截面的链状结构)链通过弱范德华力结合在一起的结晶相已成为最近关注的主题,作为通往低维固体的替代途径。17 – 22 保持