XiaoMi-AI文件搜索系统
World File Search System化学粘合决定了两个看似相同的超导体的急剧临界温度差
尽管YB 6和实验室6具有相同的晶体结构,原子价电子的形象和声子模式,但它们表现出截然不同的声子介导的超导性。yb 6低于8.4 K的超导导,使其成为已知硼化物的第二个最高临界温度,仅次于MGB 2。实验室6直到接近 - 绝对零温度(低于0.45 K)才能超导。尽管以前的研究已经量化了Yb 6的更高费米 - 水平(E F)状态和较高的电子 - Phonon耦合(EPC)的规范超导性描述(EF),但尚未全面评估该差异的根源。通过化学键合,我们确定灯笼中的低谎言,未占用的4F原子轨道是这些超导体之间的关键区别。这些轨道在YB 6中无法访问,与πB– B键杂交,并使能量的能量低于σB-B键,否则在E f时。这种频段的反转至关重要:我们显示的光学声子模式负责超导性,导致Yb 6的σ-轨道在重叠中发生巨大变化,但彼此弱于实验室6的π轨道。yb 6中的这些声子甚至访问电子状态的交叉,表明EPC强。在实验室6中未观察到这种交叉。最后,显示了一个超级电池(m k-点)会发生PEIERL-喜欢YB 6中的效果,从柔软的声音子和相同的电子 - 耦合的光学模式中引入了其他EPC。总体而言,我们发现实验室6和YB 6具有从根本上不同的超导性机制,尽管它们差不多 - 身份差。
癌症是肿瘤疗法的革命
可以根据各种标准(包括物理特性和冷却成本)对超导体进行分类。** I型超导体**:具有一个临界场(HC),并在达到超导状态和正常状态之间突然过渡。** II型超导体**:拥有两个临界场HC1和HC2,它们是下部临界场以下的完美超导体,并返回到上临界场高于上方的正常电导率。包括无法使用BCS理论或相关理论来解释的重费超导体。这些材料具有独特的特性,可以无视传统的理解,并需要进一步的研究以充分理解其行为。超导体根据其临界温度分为三组:低温超导体(LTS)低于77K,高温超导体(HTS)高于77K,而室温超级导体。77K的分界点显着,因为液氮可用于在此温度下实现材料的超导性。大多数基于元素的超导体是I型,但是存在一些例外,例如niobium,Technetium和某些碳同素同素同素。合金等合金具有超导性能。陶瓷,包括丘比特和YBCO家族,也表现出高温超导性。其他材料(如镍和Ruddlesden-popper相似)被发现在较低温度下是超导的。超导体的分类并不详尽,并且正在进行的研究继续发现具有独特特性的新材料。基于铁的超导体,二吡啶镁,palladates和其他化合物的潜力表现出超导性的潜力。超导体的发现,例如HG3NBF6和HG3TAF6,导致了材料科学领域的重大进步。这些化合物在7 K(-266.15°C; -447.07°F)以下表现出超导性,使其对于各种技术应用都很有价值。最近的突破导致了新的超导体的发展,包括无限层镍和五重杆层方形 - 平面镍镍,这表明在绝对零以上的温度下表现出超导性。此外,科学家在理解超导性的基础机制方面取得了重大进展。例如,发现二吡啶镁(MGB2)的发现使人们对高温超导体所需的特性有了更深入的理解。随着研究人员继续探索超导体材料的前沿,他们正在发现其在尖端技术中应用的新可能性。
tomasch振荡作为拓扑超导性的差距上方签名
鉴定拓扑超导体通常涉及搜索受拓扑保护的差距模式。然而,在当前的实验环境中,仍然缺乏这些内置模式的吸烟枪证据。在这封信中,我们建议通过上面的差距运输签名来支持二维常规S波和拓扑P波 - 超导体之间的区别。我们的方法利用了在两个金属铅之间夹着的超导体组成的连接中的准颗粒振荡的出现。我们证明,电导中振荡随界面屏障的函数的行为为S波和P波超导体提供了独特的签名。具体而言,随着S波超导体的屏障强度的增加,振荡变得较弱,而它们在P波超导体中变得更加明显,我们被证明是配对对称性的直接表现。我们的方法可以作为通过上述差距运输来识别某些类别的拓扑超导体的免费探针。
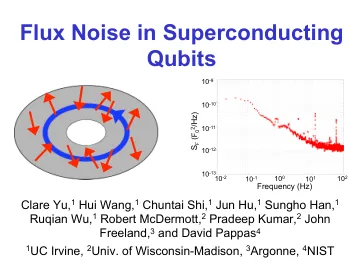
超导QUBITS中的通量噪声
如果我们将2个超导体彼此隔开,则被薄绝缘层隔开,则两个超导体之间的相位差(θ2-θ1)将导致超导库珀对的电流在超导体之间流动。电流没有电池!这是约瑟夫森效应。
物理798C春季2024讲座2摘要
要在普通金属中诱导直流电流,您可以使用直流电场。要在超导体中诱导直流电流,您可以应用直流磁场!我们从伦敦的第一个方程式中看到,电场控制了超电流的加速度。超导体在零频率下的无限电导率(在下一个讲座中进行了讨论)意味着超导体不能支持直流电场。方程式还说,需要一个交流电场来建立和支撑超导体中的交替电流。由于超导电子的有限惯性,该交流电场也将被任何共存的正常电子见证,从而造成耗散。下面是一张表,总结了(在局部极限的超导体和正常金属的简化本构方程)。
超导体 - 触发器系统中的Andreev and Majorana结合状态的非热零能量
在有限长度的超导型杂种系统中,Majorana结合状态的出现已预测以振荡能水平的形式发生,而奇偶校验横梁围绕零能量。每次零能量交叉都有望产生量化的零偏置电导峰值,但有几项研究报告了电导率峰值固定在零能量的一系列Zeeman领域,但其起源并不清楚。在这项工作中,我们考虑在Zeeman场下与旋转轨道耦合的超导系统,并证明,由于与Ferromagnet Lead的耦合,非富裕效应引起了Majorana和Trivial Andreev结合状态的零能量。我们发现,这种零能量固定效应是由于形成了被称为异常点的非弱势光谱退化性的,其出现可以通过非热性的相互作用,应用的Zeeman Fierd和化学势来控制。此外,根据非热空间空间验证,我们发现非热性会改变单点赫尔米尔拓扑相变为受到多个低能水平的特殊点的特殊点界定的零能量线。这种看似无辜的变化显着使差距截断远低于Hermitian拓扑相过渡,这原则上可以简单地实现。此外,我们揭示了将主要和琐碎的Andreev结合状态与准核定状态分开的能量差距对于产生零能量固定效应的值仍然是强大的。因此,我们的发现对于理解Majorana设备中微不足道和拓扑状态的零能量固定可能很有用。尽管合理的非热性价值确实可以是有益的,但非常强大的非热效应可能会破坏超导性。
在二阶拓扑超导体中具有Majoraana角状态的磁性拓扑编织
拓扑量子计算可以通过将逻辑信息编码为具有非亚伯统计的任何人[1,2]来消除变形,并被认为是实现耐断层量量子计算机的最有效方法。Majorana零模式的行为就像Majorana Fermions一样,每种模式都是自身的反粒子[3],并承诺一个平台来实现代表非亚洲编织组的代表,从而实现拓扑量子计算[4,5]。然而,在实验系统(例如非常规超导体[6,7])中,Majorana零模式是否诱导零能量信号[8-13],铁磁原子链[14]和二维超导管vort vort [15,15]。无论如何,它不会影响Majorana零模式编织设计的探索。后来,还提出了高阶拓扑阶段作为物质的新拓扑阶段,其在多维维度下具有非平凡边界状态。例如,Langbehn等人。提出了二维二阶拓扑超导体,以实现零维的零零模式[17]。通过应用外部磁场[18-20],可以将一阶式托架超导体驱动为二阶对应方,其中局部Majorana零模式出现在拐角处[21 - 24]。要实现Majorana零模式的编织操作,关键过程是绝热时间依赖的
arxiv:2410.21682v1 [cond-mat.supr-con] 2024年10月29日
自旋 - 轨道耦合和超导性的组合在ISIS级超导体中诱导了非常规的自旋 - 三个相关性。我们从理论上研究了通过非金属 - 金属超导体结的自旋转运,这表明Ising超导体也具有自旋超导性的特征。由于存在自旋三曲,库珀对,不仅充电超电流,而且自旋超电流可以在Ising超导体中运输。我们分析了连接中的运输过程,该交通过程主要由等旋转的Andreev反射和旋转反射,并计算不同条件下的自旋电导和自旋注射效率。我们的发现拓宽了自旋超导的边界,并揭示了Ising超导体在Spintronics中的潜在应用,尤其是在受控的长距离耗散无自旋转运中。
arxiv:2503.08162v1 [cs.ro] 2025年3月11日
手性材料表现出自旋滤波效果,所谓的手性诱导的自旋选择性(CISS)。最近观察到手性超导体末端的自旋积累的观察到了研究超导体中CISS效应的新途径。在手性超导体中,旋转单链和自旋三阶阶参数的混合物显着影响超导性的特性。在本文中,我们研究了超导顺序参数与超电流诱导的自旋电流之间的相互作用,即超传递电流。在弱聚会混合的超导体中,自旋电流主要与温度无关,是由自旋极化的库珀对带有有限的质量中心动量的。相反,在强派对混合的超导体中,温度依赖性自旋电流还由具有相反动量的电子和反平行旋转形成库珀对。手性结构化超导体将为探索CISS效应提供新的平台,并可以更深入地了解其与平均混合订单的基本机制。








![arxiv:2410.21682v1 [cond-mat.supr-con] 2024年10月29日](/simg/8\8bdb2b5de6833ca8b78e5775b95f827d36f69b3f.webp)
![arxiv:2503.08162v1 [cs.ro] 2025年3月11日](/simg/3\3943054da3ddb9b62e2dcafab078c9b4bc23d7a8.webp)