XiaoMi-AI文件搜索系统
World File Search System辅因子
转录辅因子PC4小分子抑制剂在非小细胞肺癌防治中的疗效
人类正辅激活因子 4 (PC4) 最初被鉴定为一种多功能辅因子，能够介导多种基因和组织特异性激活剂的转录激活。最近的研究表明，PC4 还可以作为不同类型癌症的新型癌症生物标志物和治疗靶点。siRNA 敲低研究表明，PC4 表达的下调可抑制裸鼠 A549 非小细胞肺癌肿瘤模型的致瘤性。这里我们表明，通过高通量筛选鉴定出的小分子 AG-1031 可以抑制 PC4 的双链 DNA 结合活性，比其单链 DNA 结合活性更有效。使用纯化的转录因子，AG-1031 还在体外特异性抑制 PC4 依赖性转录激活。 AG-1031 抑制了几种非小细胞肺癌 (NSCLC) 培养细胞系的增殖，以及免疫功能低下的小鼠中 A549 细胞异种移植瘤的生长。此外，在这些小鼠中预先注射 AG-1031 不仅可以缩小肿瘤大小，还可以防止 20% 的动物形成肿瘤。AG-1031 处理的 A549 细胞和 AG-1031 处理动物的肿瘤显示 PC4 和 VEGFC 水平显著下降，而 VEGFC 是癌症血管生成的关键介质。另一方面，所有测试小鼠在动物试验期间体重保持不变。这些结果表明 AG-1031 可能是 PC4 阳性 NSCLC 的潜在疗法。
氮酶辅因子生物合成，使用在酿酒酵母的线粒体中产生的蛋白质
抽象的生物氮固定，惰性N 2向代谢可触发的NH 3的转化仅由某些称为重18zotrophs的微生物进行，并由氮酶催化。a [7fe-9s-c-mo- r- homocitrate] - cofactor（指定为femo-CO）提供了催化位点，用于降低mo依赖性氮酶的n 2。因此，在模型真核生物（例如酿酒酵母）中实现FEAMO-CO形成，这是使它们具有MO依赖性生物氮固定能力的重要里程碑。femo-CO组装中的中心播放器是脚手架蛋白Nifen，在该蛋白质中，NIFB的[8FE-9S-C]前体的nifb-Co处理。先前的工作确定可以在酿酒酵母线粒体中产生NIFB-CO。在当前的工作中，在酿酒酵母中表达了来自不同重18zotrophs的Nifen基因的库，针对线粒体，并针对产生可溶性硝基蛋白质复合物的能力进行了调查。许多这样的nifen变体在重生A. vinelandii中异源产生时，都支持FEMO-CO形成。然而，其中只有三个以可溶性形式积聚在有氧培养的酿酒酵母的线粒体中。在体外FEAM-CO合成测定中有两个变体活跃。Nifen，Nifb和NIFH蛋白（所有这些物种都从酿酒酵母线粒体中产生并纯化），以建立成功的FEMO-CO生物合成途径。这些发现表明，将各种种间氮酶Feemo-CO组件组件结合在一起可能是一种有效的，也许是实现和优化真核眼球生物体中氮固定的唯一方法。
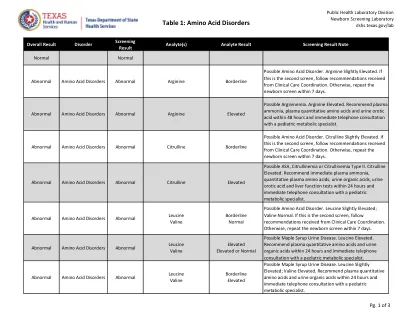
表1：氨基酸疾病 推广者（A）或社区卫生工作者（CHW）培训和... 如何审查免疫记录和德克萨斯州学校疫苗要求 表8：血红蛋白病 TVFC/ASN重新注册 负责您的健康 Texasaim Osud教师BIOS 记录疾病的历史：水痘（水痘） 新的novavax covid-19疫苗可用于订购 TVFC/ASN疫苗损失 - 报告浪费或过期... 疫苗分配和订购系统（VAO） 您可能对狂犬病不了解的8件事，但应 表1：德克萨斯州心血管疾病和中风会员的出席会议于2024年5月6日星期一举行。 unidos contra la糖尿病 负责您的健康 hep b妈妈 咨询委员会名称
可能的PKU，良性的热丙氨酸血症，辅因子生物合成或辅因子再生中生物蛋白缺损中的生物蛋白缺损。苯丙氨酸略有升高； phe/tyr抬高。在24小时内建议血浆定量氨基酸，并立即与儿科代谢专家进行电话咨询。
Mancilla Uribe J，J，Estrada Caceres E，E，Fonseca Escobar d d。急诊中颌面创伤中口服抗凝治疗的患者逆转
通过与血液接触，将因子XII转换为XIIA（激活），从而激活了XI XI因子XI向因子Xia的转化，从而将因子Xi催化为Xia，从而将因子IX裂解为IXA。XIIA还将prekallikrein转换为Kallikrein，以在正反馈循环中产生更多因子XIIA。因子IXA随后与其辅因子VIII结合，该复合物将激活因子X到Xa，这是公共途径的开始。因子Xa随后与其辅因子因子V结合，将凝血酶原（因子II）转换为凝血酶（因子IIA）。凝血酶最终将纤维蛋白原转化为纤维蛋白，开始凝块形成。10
化学计量矩阵左零空间的凸基导致了具有代谢意义的池的定义
摘要 计量矩阵 S 表示反应速率向量到浓度时间导数空间的映射。计量矩阵的左零空间包含动态不变量：浓度变量的组合，称为代谢池，其总浓度不会随时间而变化。通过类比 S 形成的传统反应图，可以从 ST 得出化合物图。与 S 的（右）零空间的通量分析类比使我们能够将代谢池分为三类：A 类包含以某些部分形式的化学元素及其组合，B 类除了包含网络内部携带此类部分的辅因子外，还包含此类部分，C 类仅包含辅因子。左零空间基的凸公式使我们能够将代谢池直接分为这三类。 B 型代谢池包括保守池，这些池形成代谢物和辅因子的部分占据和部分空置浓度状态的结合物。因此，B 型代谢池描述了主要底物和辅因子之间捕获能量和氧化还原电位等特性的部分交换的各种状态。凸基可以清楚地洞察人类红细胞中糖酵解途径的这种交换，包括识别形成结合物的高能池和低能池。示例表明，池图可能比通量图更适合信号通路。对化学计量矩阵左零空间的分析使我们能够定义细胞的可实现状态及其生理相关性。
生物化学博士入学考试大纲
酶催化反应中辅因子和辅酶的化学性质和参与，金属激活的酶和金属酶，无辅因子的酶催化反应机理。活性位点，结合位点和催化位点的识别。初速度和底物浓度之间的关系，Michaelis-Menten 方程，Lineweaver-Burk 和 Eadie-Hofstee 图，动力学数据分析，数值练习。可逆和不可逆酶抑制，酶抑制的用途。