机构名称：
¥ 1.0
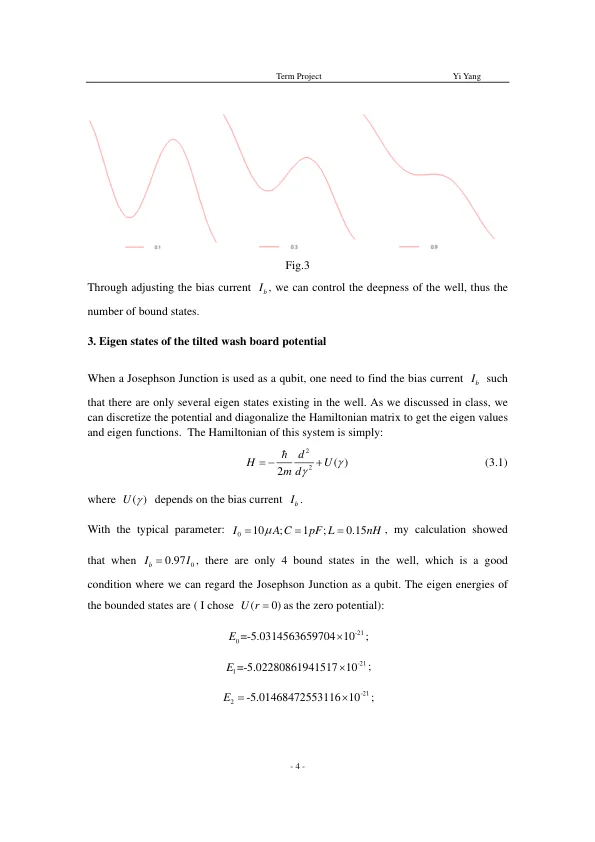
与谐振子势不同，洗衣板势的能量空间并不相等。这是该系统的一个重要特性，使其成为量子比特的候选者，这一点后面会讨论。图 4 显示了我计算中的势和 4 个最低状态的特征函数。特征函数看起来与谐振子势的特征函数相似。但是，我们可以看到，在状态 2 和状态 3 的函数右边缘，函数不再为零。事实上，由于阱的右势垒不是无限高的（实际上在这种情况下非常低），所以每个状态都必须有一个传输速率（或量子隧穿速率）。从函数草图中，我们可以粗略地看出，状态 2 和 3 的隧穿速率比状态 0 和 1 的隧穿速率大得多。实际上，这种隧穿速率的差异是我们设计具有约瑟夫森结的量子比特的另一个基础。在下一节中，我将计算每个状态的隧穿速率，并解释如何通过量子隧穿来测量这种量子比特的状态。
约瑟夫森结的量子图
主要关键词
相关文件推荐
