机构名称：
¥ 1.0
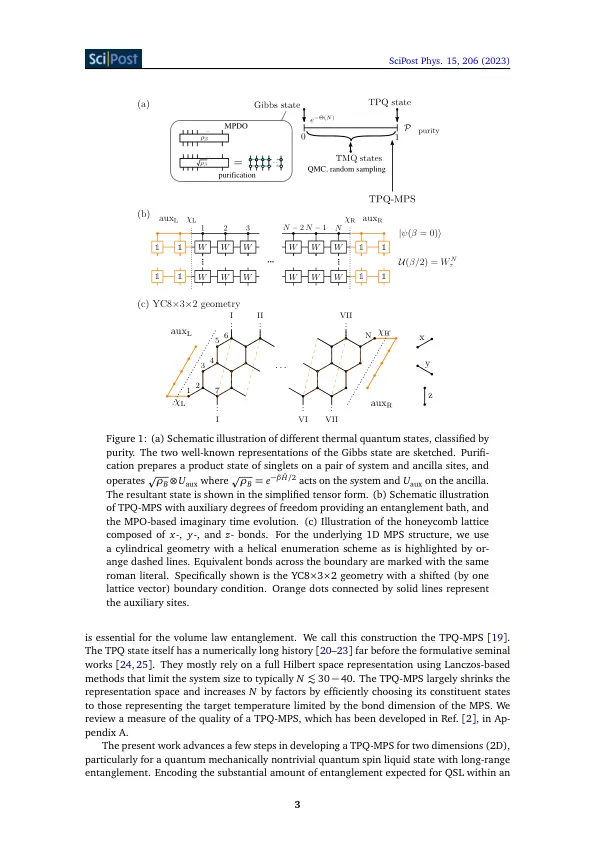
我们介绍了矩阵乘积状态（MP）的首次成功应用，该矩阵乘积状态（MPS）代表在整个温度范围内的两个空间维度中平衡中的热量子纯状态（TPQ）。我们将Kitaev Honeycomb模型用作主持量子自旋液体（QSL）基态的突出例子，以使用先前几乎完全使用Free Majorana Fermionic描述来瞄准两个先前已解决的特定热峰。从高温随机状态开始，我们的TPQ-MPS框架精确地再现了这些峰，这表明基于自旋的量子多体外描述仍然可以捕获Z 2量规场中的新出现的巡回Majorana fermions。截断过程有效地丢弃了高能状态，甚至达到了远程纠缠的拓扑状态，接近给定有限尺寸群集的确切基态。TPQ-MP的优点比精确的对角度或基于纯化的方法的优势是，即使在有限温度下，其数值降低的成本也来自降低的效率希尔伯特空间。
二维的热纯矩阵乘积状态
主要关键词
相关文件推荐
