XiaoMi-AI文件搜索系统
World File Search System期刊集合列表A-Z
A 4OR Abdominal Radiology Accreditation and Quality Assurance Acoustical Physics Acta Applicandae Mathematicae Acta Biotheoretica Acta Diabetologica acta ethologica Acta Geotechnica Acta Informatica Acta Mathematica Hungarica Acta Mathematica Sinica, English Series Acta Mathematicae Applicatae Sinica, English Series Acta Mechanica Acta Mechanica Sinica Acta神经外尿神经病理学神经病理学管理和心理健康和心理健康服务的政策研究研究的吸附在应用的克利福德代数方面的进步大气科学的进步计算数学的进步数据分析和分类在健康科学科学领域的进步进步社会协会和行为代数和逻辑代数环球代数和代表理论算法算法Alpine Alpine植物学美国舞蹈治疗杂志氨基酸氨基酸氨基酸类模拟循环和信号处理分析数学分析分析和生物分析性化学和生物分析性化学化学化学动物(henri poincaTion Annales henri poincare annalali Matata pura)金融组合纪念碑的生物医学工程年鉴
季度新闻通讯
新开设的课程: 课程名称:算子理论和算子代数 课程:博士(数学) 讲师:Harsh Trivedi 博士和 Ratan Giri 博士 学习目标:这是一门入门课程。它可应用于数学研究的几个领域,包括微分方程、量子统计力学、量子信息论和数学物理。它主要面向希望在算子理论、算子代数和相关领域进行研究的学生。 课程名称:李代数 课程:博士(数学) 讲师:Ashish Mishra 博士 学习目标:本课程介绍李代数理论。我们的目标是研究有限维复半单李代数的结构及其表示理论。李代数是一个重要的研究领域,在数学的各个领域有着广泛的应用,例如微分几何、组合学、数论、微分方程,以及物理学的许多领域,如量子力学和粒子物理学。为了给学生提供学习李代数高级主题的背景知识,本课程将从模块理论的介绍开始,特别介绍模块的张量积和张量代数的主题。本课程主要面向希望在李代数和相关领域进行研究的学生。
ERC 科学描述符
物理科学与工程 PE1 数学:数学的所有领域,包括纯数学和应用数学,以及计算机科学的数学基础、数学物理和统计学 PE1_1 逻辑与基础 PE1_2 代数 PE1_3 数论 PE1_4 代数和复几何 PE1_5 几何 PE1_6 拓扑 PE1_7 李群、李代数 PE1_8 分析 PE1_9 算子代数和泛函分析 PE1_10 ODE 和动力系统 PE1_11 偏微分方程的理论方面 PE1_12 数学物理 PE1_13 概率 PE1_14 统计学 PE1_15 离散数学和组合数学 PE1_16 计算机科学的数学方面 PE1_17 数值分析 PE1_18 科学计算和数据处理 PE1_19 控制理论与优化 PE1_20 数学在科学中的应用 PE1_21 数学在工业和社会生活中的应用 PE2物质的基本成分:粒子、核、等离子体、原子、分子、气体和光学物理学 PE2_1 基本相互作用和场 PE2_2 粒子物理学 PE2_3 核物理学 PE2_4 核天体物理学 PE2_5 气体和等离子体物理学 PE2_6 电磁学 PE2_7 原子、分子物理学 PE2_8 超冷原子和分子 PE2_9 光学、非线性光学和纳米光学
Bangabasi学院数学系
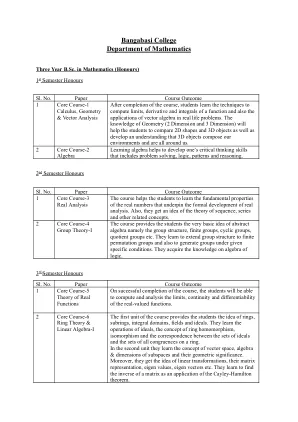
该课程的第一单元为学生提供了戒指,子环,整体域,字段和理想的想法。他们学习理想的运作,戒指同态的概念,同构的概念以及理想集和所有一致性的一组之间的对应关系。在第二个单元中,他们学习了矢量空间,代数和尺寸的子空间和几何意义的概念。他们学会找到矩阵的倒数作为Cayley-Hamilton定理的应用。
R. A. Hill的编码理论的第一门课程
用于立即或同时在代数中进行教学编码理论,因为它与具体的示例加强了线性代数和基础群体理论中涉及的许多思想。)我还将整个文本用作硕士课程,该课程不一定在数学上。最后八章在很大程度上是彼此独立的,因此可以改变课程以适合要求。例如,不是专业数学家的学生可能会省略第9、10、14和15章。
B.Tech教学大纲 - 计算机科学与工程
方程。5。了解相关,回归,力矩,偏度以及峰度和曲线拟合的概念。模块1:拉普拉斯变换:(8小时)拉普拉斯变换的定义,存在定理,衍生物和积分的拉普拉斯变换,初始和最终值定理,单位步长函数,diracdelta函数,dirac-delta函数,laplace的周期性函数,周期性拉普拉斯转换,互惠变换,卷积变换,互惠定理,solude for solve lineal lineal lineal lineal lineal lineal lineal lineal lineal lineal lineal lineal lineal areviations lineal lineal areviations lineal lineal areviations。模块2:傅立叶变换:(8小时)傅立叶积分,正弦和余弦积分,傅立叶积分,傅立叶变换,逆傅里叶式扭转,卷积定理,傅立叶定理,傅立叶正弦和余弦变换,傅立叶变换的应用到简单的一维热传输方程。模块3:代数和超验方程和插值的解决方案:(8小时)数量及其准确性,代数和先验方程的解决方案:分配方法,迭代方法,Newton-Raphson方法和Regula-Falsi方法。这些方法的收敛速率(没有证据),插值:有限差异,操作员之间的关系,使用牛顿的前向和后差公式进行插值,与不平等间隔的插值:牛顿的分裂差异和Lagrange的公式。
教学大纲
方程。5。了解相关,回归,力矩,偏度以及峰度和曲线拟合的概念。模块1:拉普拉斯变换:(8小时)拉普拉斯变换的定义,存在定理,衍生物和积分的拉普拉斯变换,初始和最终值定理,单位步长函数,diracdelta函数,dirac-delta函数,laplace的周期性函数,周期性拉普拉斯转换,互惠变换,卷积变换,互惠定理,solude for solve lineal lineal lineal lineal lineal lineal lineal lineal lineal lineal lineal lineal lineal areviations lineal lineal areviations lineal lineal areviations。模块2:傅立叶变换:(8小时)傅立叶积分,正弦和余弦积分,傅立叶积分,傅立叶变换,逆傅里叶式扭转,卷积定理,傅立叶定理,傅立叶正弦和余弦变换,傅立叶变换的应用到简单的一维热传输方程。模块3:代数和超验方程和插值的解决方案:(8小时)数量及其准确性,代数和先验方程的解决方案:分配方法,迭代方法,Newton-Raphson方法和Regula-Falsi方法。这些方法的收敛速率(没有证据),插值:有限差异,操作员之间的关系,使用牛顿的前向和后差公式进行插值,与不平等间隔的插值:牛顿的分裂差异和Lagrange的公式。模块4:数值差异和集成和解决方案:(8小时)
B.Tech的教学大纲
方程。5。了解相关,回归,力矩,偏度以及峰度和曲线拟合的概念。模块1:拉普拉斯变换:(8小时)拉普拉斯变换的定义,存在定理,衍生物和积分的拉普拉斯变换,初始和最终值定理,单位步长函数,diracdelta函数,diracdelta函数,laplace的周期性函数,周期性的拉普拉斯转换,逆向拉普拉斯变换,卷积变换,卷积定理,应用程序lineal linear lineal lineal lineal lineal lineal lineal lineal lineal lineal lineal lineal lineal areviations lineal lineal areve lineal lineal areviations。模块2:傅立叶变换:(8小时)傅立叶积分,正弦和余弦积分,傅立叶积分,傅立叶变换,逆傅里叶式扭转,卷积定理,傅立叶定理,傅立叶正弦和余弦变换,傅立叶变换的应用到简单的一维热传输方程。模块3:代数和超验方程和插值的解决方案:(8小时)数量及其准确性,代数和先验方程的解决方案:分配方法,迭代方法,Newton-Raphson方法和Regula-Falsi方法。这些方法的收敛速率(没有证据),插值:有限差异,操作员之间的关系,使用牛顿的前向和后差公式进行插值,与不平等间隔的插值:牛顿的分裂差异和Lagrange的公式。