XiaoMi-AI文件搜索系统
World File Search System在激发状态下的量子保真度敏感性...
由于其两维的性质以及存在两个良好的物理极限 - 线性和弯曲的配置,以及中间性构造 - 质中性物种 - 质膜(Quasilinear)物种 - 由大峰值运动使其富有谱图,因此,的研究已被促进了自由度的研究。 Positive or non-monotonous anaharmonicities, the latter associated with the occurrence of the Dixon dip in the Birge-Sponer plot for nonrigid molecules [2], and anomalous ro- tational spectra due to the mixing of linear and bent characters in the wave functions of states straddling in the propinquity of the barrier to linearity [3, 4] are the most salient spectroscopic features可以在准线性物种的光谱中找到。 光谱法的显着进步和发展使得一些分子物种的高弯曲泛音的实验访问可能。 以这种方式,有可能访问实验光谱信息,从而可以在线性屏障周围研究系统[5,6]。 水[7]和NCNC [8-10]获得的结果特别相关。 最近,Cushman和Duistermaat [11]最初引入的量子单片概念并由Child [12]重新审视,这在波浪函数复杂性的系统中的分配大大帮助了状态,这是由于国家邻近的障碍与线性的障碍,妨碍了状态性的状态,妨碍了一个状态标记[5-8,13]。 这一领域的开创性作品是Hougen-Bunker-Johns Bender Hamiltonian [15]。的研究已被促进了自由度的研究。Positive or non-monotonous anaharmonicities, the latter associated with the occurrence of the Dixon dip in the Birge-Sponer plot for nonrigid molecules [2], and anomalous ro- tational spectra due to the mixing of linear and bent characters in the wave functions of states straddling in the propinquity of the barrier to linearity [3, 4] are the most salient spectroscopic features可以在准线性物种的光谱中找到。光谱法的显着进步和发展使得一些分子物种的高弯曲泛音的实验访问可能。以这种方式,有可能访问实验光谱信息,从而可以在线性屏障周围研究系统[5,6]。水[7]和NCNC [8-10]获得的结果特别相关。最近,Cushman和Duistermaat [11]最初引入的量子单片概念并由Child [12]重新审视,这在波浪函数复杂性的系统中的分配大大帮助了状态,这是由于国家邻近的障碍与线性的障碍,妨碍了状态性的状态,妨碍了一个状态标记[5-8,13]。这一领域的开创性作品是Hougen-Bunker-Johns Bender Hamiltonian [15]。这是一个从经典力学借来的概念,一旦系统能量足够大以探测局部鞍点或最大值,以防止定义全球动作角变量的定义[14]。非矛盾分子物种中弯曲振动的理论建模需要特殊工具,因为较大的振幅振动自由度强烈地伴随着自由度和旋转的自由度。这项工作后来扩展到了半irigid bender hamiltonian [16]和一般的semirigid bender hamiltonian [17]。基于上述开发的模型[18]目前是分析非矛盾分子光谱的标准方法,其中同时考虑了旋转和振动自由度的同时考虑实验术语值的建模和量子标签的分配所需。代数方法,尤其是Vibron模型是传统的分子模型的传统内部差异方法的替代方法。该模型基于对称考虑因素,并在很大程度上依赖于Lie代数的特性[19]。Vibron模型(VM)属于一个模型家族,该模型分配了U(n + 1)代数为n维问题的动力学或频谱生成代数[20]。类似的模型已成功地应用于哈德子[21,22]和核[23-25]的结构的建模。2DVM定义了一种形式主义,该形式主义能够建模弯曲程度的线性和弯曲限制案例,以及表征中间情况的大幅度模式[30-33]。在原始的Vibron模型形式主义中,由Iachello引入,双子型分子物种的反振动激发被视为集体骨气兴奋[26],并且动态代数为u(3+1)= u(4),由于自由度的相关程度[25,25,27]。弯曲振动的二维性质以及简化Vibron模型形式主义以有效地处理多原子系统的需求,自然而然地驱动着vibron模型(2DVM)的二维极限的制定[28,29]。最近发表了在本工作中使用的代数哈密顿量的四体操作员的扩展[34]。2DVM也已用于耦合弯曲器的建模[28,35-37],拉伸弯曲中的相互作用[38-41]和异构反应中的过渡态[42]。
旋翼机飞行模拟模型保真度改进和...
5.4 降阶模型和基于物理的修正 5-6 5.4.1 方法论 5-6 5.4.1.1 旋翼诱导流入动力学 5-6 5.4.1.2 旋翼间干扰 5-8 5.4.1.3 气动干扰 5-9 5.4.1.4 机身气动 5-9 5.4.1.5 带旋翼超前-滞后的发动机/传动系统动力学 5-9 动力学 5.4.1.6 传感器和斜盘执行器动力学 5-10 5.4.2 应用 5-10 5.4.3 优势和局限性 5-10 5.5 基于物理的模拟的模型参数调整 5-11 5.5.1 方法论 5-11 5.5.1.1 D 级飞行员训练的参数调整 5-11模拟器 5.5.1.2 工程研究的参数调整 5-11 模拟 5.5.2 应用 5-12 5.5.3 优点和局限性 5-12 5.6 关键模拟常数的参数识别 5-12 5.6.1 方法 5-12 5.6.2 应用 5-12 5.6.3 优点和局限性 5-12 5.7 从点 ID 模型和修剪数据进行拼接模拟 5-13 5.7.1 方法 5-13 5.7.2 应用 5-15 5.7.3 优点和局限性 5-15 5.8 参考文献 5-16
建立运动保真度的初步进展...
本文介绍的研究是利物浦大学 (UoL) 正在进行的一个项目的一部分,该项目旨在开发海上旋翼机飞行模拟器的整体模拟保真度要求。这需要对单个建模和仿真 (M&S) 元素进行结构化检查,例如运动和视觉提示、飞行动力学模型和船舶尾流集成。本文报告了运动提示研究的初步结果,该研究旨在评估和优化运动驱动规律并确定模拟船上操作的高保真运动提示。为此,开发了一种客观技术,即前庭运动感知误差 (VMPE)。该技术用于优化 UoL 的 Heliflight-R 模拟器中的运动提示,以模拟直升机在湍流环境中降落在航空母舰上。离线导出了四个运动调整集并进行了实验测试。结果显示了不同运动提示和尾流条件对飞行员整体自我运动感知、控制策略和任务表现的影响。研究发现,在较高的尾流风条件下,高保真运动提示对飞行员来说更可取,使用新技术可以获得“优化”运动设置,而不是在较低的尾流湍流条件下。
CRISPR-CAS9变体保真度的动力学机制
。cc-by-nc 4.0国际许可(未获得同行评审证明),他授予Biorxiv授予Biorxiv的许可,以永久显示预印本。它是此预印本版本的版权持有人,该版本发布于2025年1月29日。 https://doi.org/10.1101/2025.01.27.634389 doi:Biorxiv Preprint
转移概率(保真度)及其相关项
本文描述了量子物理的“非动力学基础”或“语法”的一小部分,但内容却十分丰富。随着量子信息论的兴起,它的重要性比以前更加明显,尽管在量子场论和统计物理学的所谓代数方法中已经很明显了。当然,只有结合动力学、具体哈密顿量等才能取得实验进展。另一方面,我们在本文中讨论的规则是如此普遍,以至于人们几乎不敢相信它们可以从特别选择的动力学中推导出来或证明出来。与作者的观点相反,这些一般规则是设定可能形式的动力学(包括空间和时间)的条件。
第 11 讲 追踪距离和保真度
迹距的操作意义在于概率区分性。假设我们的目的是区分一个概率为p的事件P和概率为q的事件Q。一个最普遍的策略是,当j发生时,我们以概率f(j)和1-f(j)将其判断为P和Q,其中f(j)∈[0,1]。那么成功概率为“
量子态验证和保真度估计的统计方法
高效可靠的量子态认证对于各种量子信息处理任务以及量子技术实施的总体进展至关重要。近几年来,出现了几种使用高级统计方法以资源高效的方式认证量子态的方法。本文回顾了该领域的最新进展。首先解释如何用假设检验的语言讨论量子态的验证和保真度估计。然后,详细解释了使用局部测量或局部操作辅助测量和经典通信来验证纠缠态的各种策略。最后,讨论了该问题的几种扩展,例如量子信道的认证和纠缠的验证。
数据压缩与有线的信号保真度权衡...
摘要 - 途径高密度和高通道计数神经接口,能够同时记录成千上万的神经元的同时记录,将为学习,恢复和增强神经功能提供一个门户。但是,在完全植入的设备的比特率极限和功率预算内建立此类技术是具有挑战性的。使用在类似物到数字界面处使用有损耗的压缩,有线或压缩读数架构解决了高通道计数神经界面的数据洪水挑战。在本文中,我们评估有线或对神经工程至关重要的几个步骤的适用性,包括尖峰检测,尖峰分配和波形估计。对于有线或有线信号的各种接线配置以及基础信号质量的假设,我们表征了压缩比和特定任务信号保真度指标之间的权衡。使用来自猕猴视网膜中的18个大尺度微电极阵列记录的数据,我们发现,对于7-10的事件SNR,有线或正确检测并分配了至少80%的尖峰,至少具有50倍压缩。有线或方法还鲁棒地编码动作电势波形信息,从而实现了下游处理,例如细胞类型分类。最后,我们表明,通过将基于LZ77的无损耗压缩机(GZIP)应用于有线或体系结构的输出,可以在基线记录中实现1000倍压缩。
具有保真度估计的可扩展量子断层扫描
随着量子器件制造技术的快速发展,我们现在可以操纵越来越多的纠缠量子比特。中型量子器件(10-100 量子比特)已在超导电路、囚禁离子和超冷原子平台上实现 [1-7]。量子态层析成像 (QST) 旨在通过对状态副本进行适当测量来重建未知量子态,它是验证和衡量实现优劣的黄金标准。具体而言,QST 是证明量子处理器上所有实际操作和测量所能提供的信息的完整性所必需的。量子场论的早期研究集中在混合态,发现它需要对一组最小 O(d) 个互不偏基进行射影测量[8-10],或对正算子值测度(POVM)进行 O(d2) 期望所提供的信息[11-14]。随着希尔伯特空间维数 d 随着成分(如粒子)数量的增加而呈指数增长,这很快变得不切实际。对于纯态,最近证明,就信息而言,POVM 的数量可以大幅减少到 O(d)[15-17],测量基的数量可以减少到 4 个[18-20]。然而,由于样本空间 d 的大小呈指数级增长,实现这些精心设计的非局部测量并获得相应的收敛概率分布在实验上仍然是难以实现的[21]。经过长期发展其数学基础之后,我们现在正处于考虑其实用方面的阶段。
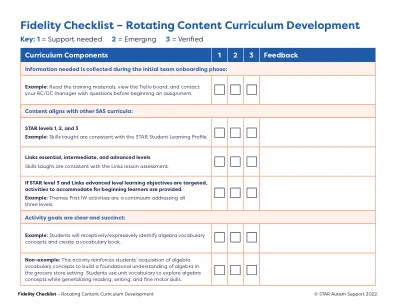
保真度检查表 – 轮换内容课程开发
非示例:此活动强化学生对代数词汇概念的掌握,以在杂货店环境中建立对代数的基本理解。学生使用单位词汇探索代数概念,同时概括阅读、写作和精细运动技能。