XiaoMi-AI文件搜索系统
World File Search System比特币区块链中使用的SECP256K1椭圆曲线的安全性:
摘要:本文深入研究了用于比特币区块链中地址生成的SECP256K1椭圆曲线的复杂特征和安全属性。比特币区块链是一个分散的数字分类帐,记录了用比特币加密货币进行的所有交易。在这项工作中,描述了SECP256K1椭圆曲线及其参数以及使用随机数生成私钥和公共密钥的方法。虽然专用密钥允许签署交易来花费比特币,但相应的公钥和地址使其他人能够验证交易并将资金发送到区块链上的特定地址,以确保分散网络中的安全性,真实性和隐私性。讨论了对使用SECP256K1的使用来生成诸如蛮力攻击,扭曲攻击,故障攻击以及椭圆曲线实施中的侧渠道攻击之类的比特币地址。通过维护SECP256K1的安全性和完整性,我们可以确保加密操作(例如数字签名和关键交换)仍然不妥协。如果曲线的安全性受到了损害,恶意用户可能会从公共钥匙中衍生出私钥,从而导致未经授权的交易,双人支出或其他恶意活动。可以通过确保使用SECP256K1进行彻底的测试和验证以确保正确且安全的操作来增强实施的安全性。讨论了对区块链技术的重要攻击,例如51%的攻击,SYBIL攻击,双重支出攻击和智能合同漏洞。通过全面的探索,读者将了解为什么选择这种特定的椭圆曲线以用于比特币的加密协议中,从而强调了其在确保区块链生态系统的鲁棒性和完整性方面的作用。
优秀男子铁饼投掷技术的时间分析
希腊塞萨洛尼基亚里士多德大学体育与运动科学系生物力学实验室 摘要 Panoutsakopoulos V, Kollias IA。优秀男子铁饼投掷技术的时间分析。J. Hum。Sport Exerc。Vol.7,No.4,页826-836,2012。本研究的目的是调查一组优秀男子铁饼运动员的投掷时间与官方投掷距离之间的关系。为了进行研究,我们分析了国际顶级田径比赛参赛者的技术阶段(即准备、入场、腾空、过渡、投掷、释放)。使用 Casio EX-FX1(卡西欧计算机有限公司)数码摄像机(采样频率:300fps)记录了七名右撇子投掷运动员(年龄:28.8 ± 4.1 岁,身高:1.94 ± 0.09 米,体重:119.4 ± 11.6 公斤)的投掷动作,并使用 V1 Home 2.02.54 软件(Interactive Frontiers Inc.)分析了捕捉到的投掷动作,从而获取了数据。使用 SPSS 10.0.1 软件(SPSS Inc.),通过皮尔逊相关分析检验了投掷技术阶段的持续时间与官方投掷距离之间的关系。结果显示,平均官方投掷距离(63.04 ± 6.09 米)与掷铁饼时间或每个技术阶段的时间之间没有显著相关性(p > 0.05)。时间和相关性分析与之前的研究一致。主要的投掷方式是无地面支撑的投掷。大多数投掷运动员在投掷转弯(过渡、投掷和投掷阶段)中单人支撑所占比例大于双人支撑所占比例。值得注意的是,过渡阶段持续时间短,加上起始转弯所用时间与投掷转弯所用时间之比较低,可能有利于实现更大的投掷距离。关键词:田径投掷、官方投掷距离、单支撑阶段、双支撑阶段、生物力学。
量子二十一点:量子策略在通信受限游戏中的优势
在量子信息领域,双人博弈为我们展示了量子纠缠作为一种资源的独特威力。例如,克劳塞-霍恩-西莫尼-霍尔特 (CHSH) 博弈就是一个操作任务的例子,其中量子纠缠比所有可能的经典策略都更具优势。对 CHSH 以及更一般的非局部博弈的分析不仅为我们提供了对贝尔不等式 [1] 等基础概念的洞察,而且还为可验证随机性生成 [2]、密钥分发 [3] 和委托计算 [4] 等重要任务制定了协议。由于无需通信的纠缠就能产生超出经典可能性的相关性,因此值得探索在允许通信的情况下这种相关性在多大程度上仍然成立。对于具有分布式输入的计算函数,纠缠可以将通信成本降低多达指数倍 [5],但不会更多 [6]。纠缠形式在某些情况下很重要,但在其他情况下则不然:当允许通信和少量误差时,爱因斯坦-波多尔斯基-罗森对至少与其他状态一样有用 [ 7 ],而在零通信设置中,非最大纠缠态可以实现更多 [ 8 , 9 ]。虽然这些结果告诉我们通信量为零或渐近增长,但对于特定协议的非渐近通信量知之甚少。我们将在此基础上构建的一个例外是参考文献 [ 10 ] 的“超比特”协议,它表征了具有无限纠缠、单个比特通信和单个比特输出的协议的功能,得到的答案让人想起了 Tsirelson 对 XOR 游戏的表征[ 11 , 12 ]。其他非渐近结果包括通信减少的具体例子(例如,使用纠缠从 3 比特减少到 2 比特[13])、随机接入编码中的量子优势[14,15]、量子通信功率与贝尔不等式的关系[16,17]、补充有 1 比特通信的局部隐变量模型[18],以及针对大型纠缠的低通信测试
单向量子通信的直接乘积定理
其中 Q1ε(f)表示最坏情况误差为ε的f的单向纠缠辅助量子通信复杂度,fk表示f的k个并行实例。据我们所知,这是第一个用于一般关系量子通信复杂度的直接积定理——直接和定理以前仅用于一般关系的单向量子协议,而直接积定理仅在特殊情况下为人所知。我们的技术受到Jain、Pereszlényi 和Yao [ 24 ]提出的乘积分布下的双人非局部博弈中纠缠值的并行重复定理,以及Bavarian、Vidick 和Yuen [ 4 ]提出的锚定分布下的并行重复定理,以及Jain、Radhakrishnan 和Sen [ 29 ]提出的量子协议消息压缩的启发。具体来说,我们证明了对于 X × Y 上任意锚定在一侧的分布 q 下,f 的分布单向量子通信复杂度的直积定理成立,即存在 ay ∗ 使得 q(y ∗) 为常数,且对于所有 x ,q(x|y ∗)=q(x)。这使我们能够证明一般分布的直积定理,因为对于任何关系 f 及其输入上的任何分布 p,我们可以定义一个修改的关系 ˜ f ,它具有接近于 p 的锚定分布 q,使得对于 ˜ f 在 q 下失败的概率最多为 ε 的协议可以用来给出对于 f 在 p 下失败的概率最多为 ε + ζ 的协议。我们的技术也适用于纠缠的非局部博弈,这些博弈的输入分布锚定在任意一侧,即,要么存在前面指定的 ay∗,要么存在一个 x∗,使得 q(x∗) 为常数,且对所有 y 都有 q(y|x∗)=q(y)。具体来说,我们表明,对于任何博弈 G=(q,X×Y,A×B,V),其中 q 是 X×Y 上的分布,锚定概率为常数,锚定在任意一侧,则
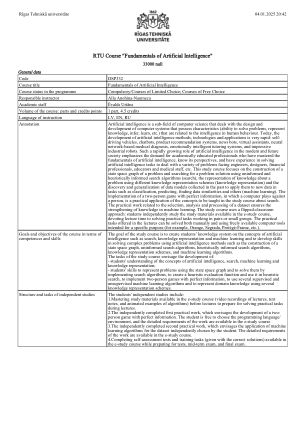
RTU课程“人工智能基础”
代码 DSP332 课程名称 人工智能基础 课程状态 必修/限选课程;自由选择课程 指导老师 Alla Anohina-Naumeca 教职人员 Ēvalds Urtāns 课程数量:课时和学分 1部分,4.5个学分 教学语言 LV, EN, RU 注释 人工智能是计算机科学的一个子领域,涉及设计和开发具有与人类行为智能相关的特性(解决问题、表示知识、推断、学习等的能力)的计算机系统。如今,人工智能方法、技术和应用的发展非常迅速:自动驾驶汽车、聊天机器人、产品推荐系统、新闻机器人、虚拟助手、基于神经网络的医疗诊断、情感智能辅导系统,以及令人印象深刻的工业机器人。人工智能在现代和未来社会中的作用日益增强,这凸显了对受过学术教育的专业人员的需求,他们掌握了人工智能的基础知识,了解其前景,并具有解决人工智能任务的经验,以解决工程师、设计师、金融专业人士、教育工作者和医务人员等面临的各种问题。本学习课程的重点是构建问题的状态空间图并使用无信息和启发式信息搜索算法(搜索)搜索问题解决方案,使用不同的知识表示方案表示有关问题的知识(知识表示)以及发现和概括过去收集的数据模型,以将它们应用于分类、预测、查找数据相似性等任务中的新数据(机器学习)。实施具有完美信息的双人游戏,其中计算机与人对战,是搜索学习课程中要教授的概念的实际应用。与数据集的选择、分析和处理相关的实际工作确保了机器学习知识的加强。该学习课程采用翻转课堂方式:学生独立学习电子学习课程中提供的学习材料,利用课堂时间以两人一组或小组的形式解决实践任务。课堂上提供的实际任务既可以手动解决,也可以使用免费提供的专用计算机工具(例如 Orange、Segrada、Protégé-Frame 等)解决。课程在能力和技能方面的目标和目的
博弈论基础 I:战略形式游戏 1 - CDN
博弈论是研究冲突与合作的分析框架。早期的研究工作受到赌博和国际象棋等娱乐游戏的启发,因此博弈论中出现了“博弈”一词。但很快人们就发现,该框架的应用范围要广泛得多。如今,博弈论已用于许多学科的数学建模,包括许多社会科学、计算机科学和进化生物学。在这里,我主要从经济学中举出例子。这些笔记是对一种称为战略形式博弈(也称为标准形式博弈)的数学形式主义的介绍。目前,将战略形式博弈视为代表一种非时间互动:每个玩家(用博弈论的语言)在不知道其他玩家做了什么的情况下采取行动。一个例子是双人游戏石头剪刀布的单个实例(您可能已经很熟悉,但将在下一节中讨论)。在配套笔记《博弈论基础 II:扩展形式博弈》中,我开发了一种称为扩展形式博弈的替代形式主义。扩展形式博弈明确地捕捉了时间因素,比如在标准国际象棋中,玩家按顺序移动,并且每个玩家都知道游戏中之前的动作。如我在扩展形式博弈的笔记中所讨论的,有一种自然的方式可以为任何扩展形式博弈提供战略形式表示。还有第三种形式,称为联盟形式博弈(也称为特征函数形式)。联盟形式抽象了个体玩家行为的细节,而是关注物理上可能的收益分配,既适用于所有玩家一起,也适用于每个玩家子集(联盟)。我(目前)没有关于联盟形式博弈的笔记。Osborne (2008) 是一篇关于战略和扩展形式博弈研究的简短入门文章。Gibbons (1992) 是博弈论的标准本科教材,我经常在自己的课程中使用。其他选择包括 Osborne (2003)、Watson (2013) 和 Tadelis (2013)。标准的研究生博弈论教材是 Fudenberg 和 Tirole (1991)。我还推荐 Myerson (1991)、Osborne 和 Rubinstein (1994) 和 Mailath (2019)。研究生微观经济理论教材中也有关于博弈论的很好的介绍,例如 Kreps (1990)、Mas-Colell
课程信息 2024-25 MN3119 策略
教学大纲 基础博弈论:双人博弈。静态和动态博弈以及一些例子。均衡概念和解决机制 - 纳什均衡、主导/被主导策略、逆向归纳法。寡头竞争:完全竞争和垄断。价格竞争和伯特兰悖论。数量竞争。反应函数。伯特兰与古诺。市场结构分析:描述市场结构:C4 比率、赫芬达尔指数、勒纳指数和市场力量。市场定义 - 技术和解释。勾结:卡特尔和反垄断。卡特尔稳定性和贴现因子。市场动态和勾结稳定性。战略联盟:投资组合测试。战略和商业伙伴关系。互补来源。资源积累。吸收能力。组织设计:组织契合度、战略和结构、职能组织、多部门结构、全球结构。竞争动态:竞争动态、竞争行动、资源相似性、市场共性、意识、动机和能力。战略不对称:规模经济、来源和后果。范围经济:航空枢纽。学习或经验曲线。具有 EoScale/Scope/Learning 的企业战略。先发优势。收益递增的市场结构。价值链分析和垂直关系:双重边际化及其补救措施。垂直排斥。零售商竞争和投资外部性。垂直整合和交易成本:制造或购买。合同。关系特定资产和持有。经济租金和准租金。进入和进入威慑:进入的结构性决定因素。进入壁垒和退出壁垒。进入威慑。识别进入者。研究与开发:市场结构和研发强度。研发竞争。垄断者和进入者的研发激励。研发的风险选择。专利制度的好处。沉睡专利。溢出效应。技术采用:先发制人游戏。期权价值和未来技术世代。技术传播:异质性、流行病和种群生态学方法。网络效应:直接和间接网络效应。系统产品。过剩惯性。过剩动量。具有网络效应的企业战略。标准之战。所有主题均在主题指南中通过专门编写的案例研究进行了补充。
主席页面 - 航空航天医学协会
Melchor Antuñano 主席制定的战略计划仍然有效。AsMA 行动纲领中的几项内容有助于定义和改善航空航天医学在教育和研究中的参与。五个常设委员会和几个组成组织承担了广泛的任务,直接影响我们协会的这一领域。由航空航天人为因素委员会主席 Thomas Nesthus 博士任命的一个小组委员会对“航空疲劳对策”立场文件进行了广泛研究,该文件计划于 2007 年 5 月的会议之前准备好供审查和批准。本文将考虑并报告所有可能的对策,以减少军用和民用机组人员的疲劳,并借鉴该领域许多杰出研究人员的经验和背景。由 Chuck DeJohn 博士担任主席的航空安全委员会有两个非常有成效的小组委员会。由 Mary Cimmrmancic 博士担任主席的民航安全小组委员会已经讨论了“最佳客舱高度”问题,并在 John Ernsting 博士的顾问下就此问题制定了立场文件。该小组委员会在奥兰多会议上提交了一项关于“航空医学对重大飞机事故调查的贡献”的决议。该决议已通过并通过信函传达给国际民航组织。由 Tarek Sardana 博士担任主席的军事航空安全小组委员会研究了“无人驾驶飞行器控制员医疗标准建议政策”问题(与 ASAMS 联合),并起草了一份决议供我们 5 月份的会议审议。在 Stan Mohler 博士的领导下,历史和档案委员会对年度奖项的获奖者进行了审查。这些奖项的获奖者反映了他们参与航空航天医学和相关领域的丰富历史。该委员会计划在 5 月份的会议上举行双人小组会议,重点介绍德克萨斯州布鲁克斯空军基地 (City-Base) 的研究历史,该基地将于 2011 年关闭。他们还将在新奥尔良提供具有航空医学意义的历史航空影片。由 Jan Stepanek 博士担任主席的教育和培训委员会正在努力形成一个世界性的
NASA的MN太空赠款财团(MNSGC)本科奖学金申请指示NASA的MN太空赠款财团(MNSGC)本科奖学金申请指示
•回答“ Mn Twin Cities U的MNSGC 2025年春季奖学金申请”当被问及“您要申请什么?” •上传个人陈述(一页最大,打字,双人间隔),描述您的教育和职业目标,以及它们如何直接或间接地联系NASA对太空探索的愿景和/或NASA对增加STEM(科学,技术,工程学和数学)工作中的性别和种族/种族多样性的兴趣。(要阅读有关NASA的过去,现在和未来计划的更多信息,请遵循http://www.nasa.gov的“关于NASA”的链接。)•以.pdf表单上传您的MN转录本的非官方副本。•需要来自MN教授或MN学术顾问的U的推荐信。提供他们的姓名,部门/标题和电子邮件地址(并提前告诉他们,希望与您的MNSGC奖学金申请联系,要求与请求联系)。推荐信将于2025年1月31日到期。奖学金获得者将从那些在过去的教育努力中非常成功的申请人中选择(通常GPA临界值为3.0,但我们将考虑在其他领域的GPA较低的GPA,并且他们的研究领域和职业目标与NASA在太空科学/工程领域的目标保持一致。申请人必须是MN双胞胎城市U的全日制学生,并且必须是美国公民。其他MNSGC学校为学生提供了单独的机会和不同的截止日期。请注意,重点是与NASA共享感兴趣领域的申请人。因此,除非可以清楚地将其职业目标确定为支持NASA的使命和/或可以帮助增加STEM劳动力的多样性,否则不寻求潜在从业人员在健康,医疗和兽医领域中的申请。在https://www.mnspacegrant.org上了解有关MN空间赠款的更多信息。如果您对此奖学金机会有任何疑问,请通过将电子邮件发送至mnsgc@umn.edu,联系明尼苏达太空赠款副主任詹姆斯·弗拉滕教授。UMTC学生此奖学金机会的申请截止日期是2025年1月28日,星期二(推荐信至2025年1月31日)。奖学金决定将在2月初做出,奖项将向MN学生帐户发放,并可用于在春季学期内帮助支付教育费用。
弗雷德·托尔曼指挥士官长
指挥军士长 Fred N. Tolman 是科罗拉多州布莱顿人,2002 年 5 月以步兵身份加入美国陆军。他参加了佐治亚州摩尔堡的步兵一站式部队训练。指挥军士长 Tolman 在其职业生涯中担任过多个领导和教学职位,包括火力小组组长、助理小组军士、侦察训练教官、小组军士、高级军事科学教官、营作战军士长和营指挥军士长。指挥军士长托尔曼在美国本土的任职包括佐治亚州摩尔堡的第 75 游骑兵团第 3 游骑兵营和团侦察连、第 75 游骑兵团特种部队营、马萨诸塞州波士顿大学美国陆军学员司令部第 2 旅和南卡罗来纳州杰克逊堡的第 39 步兵团第 2 营。他曾在韩国凯西营的第 503 伞兵团第 1 营、第 2 步兵师和意大利卡塞马德尔丁的第 173 步兵旅战斗队(空降)第 503 步兵团第 2 营服役。托尔曼指挥军士长曾多次被派往阿富汗、伊拉克和世界其他地区,为战斗和应急行动提供支持,积累了近六年的战斗经验。托尔曼指挥军士长的军事教育包括参加空中突击学校、空降学校、游骑兵训练计划、游骑兵学校、指定射手课程、探路者课程、军事自由落体跳伞员课程、侦察和监视领导者课程、跳伞长课程、SERE 学校、团侦察操作员培训课程、高级源操作课程、军事自由落体跳伞长课程、突破大师课程、联合军事双人跳伞大师课程、电子和信息安全课程、隐蔽进入课程、跨机构通信课程、非标准通信课程、基础教员辅导员课程、大学高级领导者课程、所有 NCOPDS 和军士长学院。托尔曼指挥军士长还获得了计算机工程理学学士学位、领导力与劳动力发展文学士学位,目前正在攻读电气与计算机工程理学硕士学位。托尔曼指挥军士长与结婚 21 年的妻子凯利和三个女儿阿拉娜、米娅和菲奥娜居住在佐治亚州摩尔堡。他的儿子尼古拉斯目前也驻扎在佐治亚州摩尔堡。