XiaoMi-AI文件搜索系统
World File Search System固体的
范德华固体的机器人四维像素组装
通过组装层状二维材料 1、2，可以设计出具有原子级精确垂直组成的范德华 (vdW) 固体。然而，由微机械剥离的薄片 3、4 手工组装结构与可扩展和快速制造不兼容。进一步设计 vdW 固体需要精确设计和控制所有三个空间维度上的组成以及层间旋转。本文，我们报告了一种机器人四维像素组装方法，用于以前所未有的速度、精心设计、大面积和角度控制制造 vdW 固体。我们使用机器人组装由原子级薄的二维组件制成的预图案化“像素”。晶圆级二维材料薄膜的生长和图案化采用清洁、非接触式工艺，并使用由高真空机器人驱动的工程粘合剂印章进行组装。我们制备了多达 80 个独立层的范德华固体，由 100 × 100 μ m 2 的区域组成，这些区域具有预先设计的图案形状、横向/垂直编程的成分和可控的层间角度。这使得对范德华固体进行有效的光学光谱分析成为可能，揭示了 MoS 2 中新的激子和吸光度层依赖性。此外，我们制备了扭曲的 N 层组件，其中我们观察到了扭曲的四层 WS 2 在≥ 4° 的大层间扭曲角下的原子重构。我们的方法能够快速制造原子级分辨的量子材料，这有助于充分发挥范德华异质结构作为新物理 2、5、6 和先进电子技术 7、8 平台的潜力。对硅等无机晶体材料的结构和化学成分进行精确的三维 (3D) 空间控制（x、y、z）是集成电路的基础。通过堆叠二维材料 (2DM) 形成的范德华 (vdW) 固体不受晶格可公度性或层间键合的限制，因此与传统的顺序沉积晶体 1、2 相比具有两个优势。首先，相邻层之间的晶格和化学灵活性意味着可以生产具有层可调电学 4、5、9、磁性 9、10 和光电 11-14 特性的任意垂直晶体组合物序列。其次，这种层间灵活性引入了一个额外的维度 θ，即层间晶格旋转或扭曲，作为控制 vdW 固体性质的新自由度。这已在
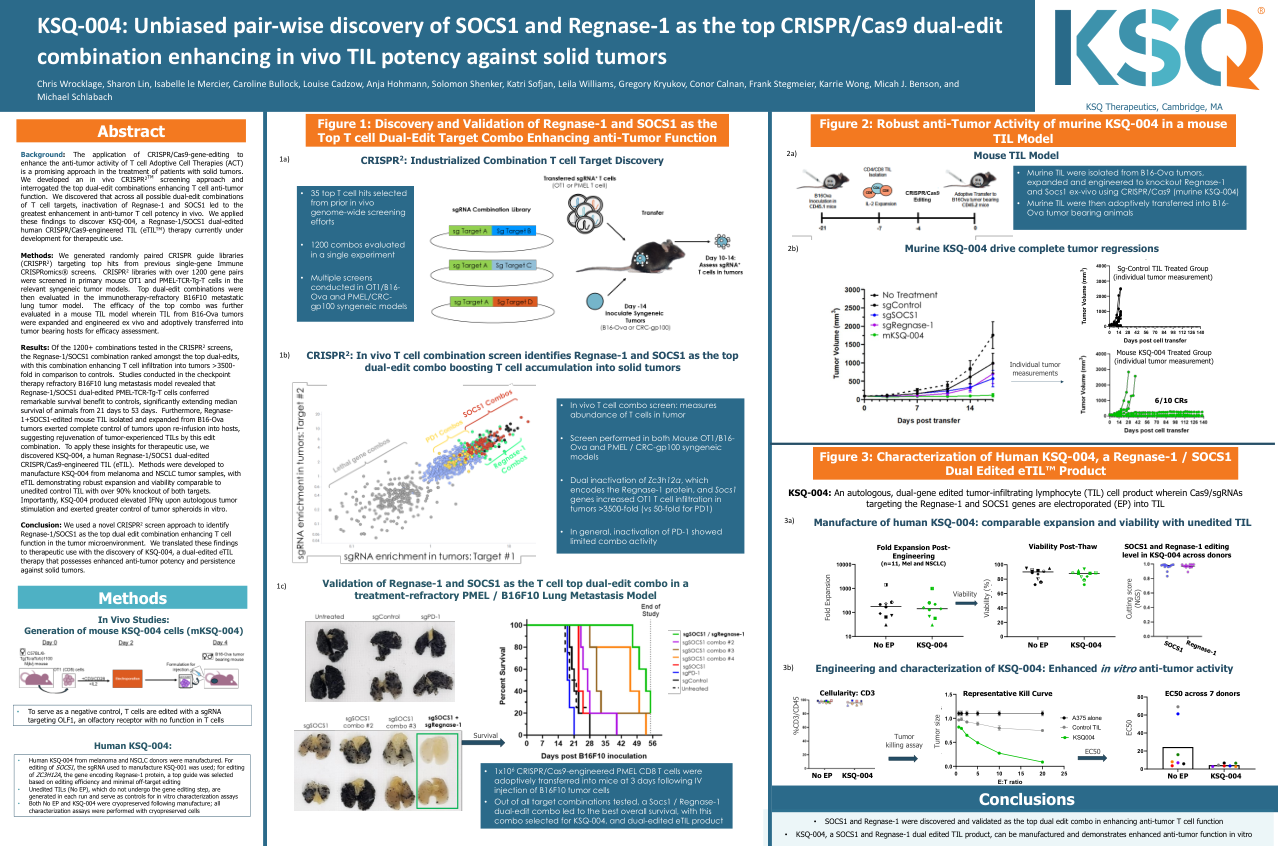
KSQ-004：无偏对发现 SOCS1 和 Regnase-1 是最佳 CRISPR/Cas9 双重编辑组合，可增强体内 TIL 对固体的效力
结果：在 CRISPR 2 筛选中测试的 1200 多种组合中，Regnase-1/SOCS1 组合位居双编辑组合之首，与对照组相比，该组合增强了 T 细胞向肿瘤的浸润 >3500 倍。在检查点治疗难治性 B16F10 肺转移模型中进行的研究表明，Regnase-1/SOCS1 双编辑的 PMEL-TCR-Tg-T 细胞为对照组带来了显著的生存优势，显著延长了动物的中位生存期，从 21 天延长至 53 天。此外，从 B16-Ova 肿瘤中分离和扩增的 Regnase-1+SOCS1 编辑的小鼠 TIL 在重新输注到宿主体内后对肿瘤产生了完全控制，表明这种编辑组合可以使肿瘤经历的 TIL 恢复活力。为了将这些见解应用于治疗用途，我们发现了 KSQ-004，这是一种人类 Regnase-1/SOCS1 双编辑 CRISPR/Cas9 工程化 TIL (eTIL)。我们开发了从黑色素瘤和 NSCLC 肿瘤样本中制造 KSQ-004 的方法，eTIL 表现出与未编辑对照 TIL 相当的强劲扩增和活力，两个靶标均被敲除 90% 以上。重要的是，KSQ-004 在自体肿瘤刺激下产生了升高的 IFNɣ，并且在体外对肿瘤球体发挥了更大的控制作用。
固体的总能量的快速准确预测...
摘要我们使用图形卷积神经网络（GCNN）来快速准确地预测固体溶液二元合金的总能量。gcnns允许我们抽象固体物质的晶格结构作为图，从而将原子建模为节点和金属键作为边缘。此表示自然结合了有关材料结构的信息，从而消除了对标准神经网络（NN）方法所需的计算昂贵数据预处理的需求。我们在Ab-Initio密度功能理论（DFT）上训练GCNN，用于铜金（CuAU）和铁铂（FEPT）数据，这些数据是通过运行LSMS-3代码而生成的，该数据实现了OLCF SuperCutisters titan and Immit的LSMS-3代码，该代码实现了本地自称的多重散射方法。gcnn在计算时间方面，按数量级胜过Ab-Initio dft模拟，以产生给定的原子结构的总能量的估计。我们通过使用根平方的误差来量化深度学习（DL）模型的预测质量，将GCNN模型与标准NN的预测性能进行比较。我们发现，GCNN的可达到的准确性至少比MLP的数量级好。
9固体的传输特性
请注意，σ和κ都是张力量，例如，沿x轴的梯度原则上可以导致沿y - 或z轴沿ux量。但是，在大多数情况下，σ和κ的这些非对角线术语是比对角线术语小的数量级，因此我们将讨论限制为本章中的对角线术语。此外，重要的是要意识到该方程。（9.1）和等式。（9.2）是J E（U）和J H（t）的完整关系的第一阶taylor扩展。就本章而言，使用这种线性响应近似值远远超过了理由，鉴于典型的电压Δu<1，000 V和温度差异∆ t <1，000 k在现实世界中应用于大型固体（量V> 1 µ M 3）对应于1 µm Minuse Elively级别的1级和一级<<1级和温度级别的<1级和温度级别的<10k。在此制度中，我们可以将所谓的“ Onsager图片”中的固体视为显微镜，各个部分的组合：假定本节的每个部分都如此之大，以至于可以保持热力学平衡规则，并允许定义温度量化，例如每个单个部分的温度。但是，各个部分相对于彼此而言并不处于热力学平衡状态。从一开始，这似乎是一个显然简化讨论的假设。我们将在本章中看到，实际上并非如此：基本原因是我们
第 3 章 / 晶体固体的结构 - UNC 物理学
衍射现象 当波遇到一系列间距均匀的障碍物时就会发生衍射，这些障碍物 (1) 能够散射波，并且 (2) 其间距在大小上与波长相当。此外，衍射是两个或多个被障碍物散射的波之间建立特定相位关系的结果。考虑图 3.1 a W 中的波 1 和 2，它们具有相同的波长 (�) 并在点 O – O � 处同相。现在让我们假设这两个波都以某种方式散射，即它们穿过不同的路径。散射波之间的相位关系很重要，它将取决于路径长度的差异。当这个路径长度差是波长的整数倍时，就会出现一种可能性。如图 3.1 a W 所示，这些散射波（现在标记为 1 � 和 2 �）仍然同相。据说它们相互加强（或相互干扰）；并且，当振幅相加时，就会产生图中右侧所示的波。这是衍射的一种表现，我们将衍射光束称为由大量相互加强的散射波组成的光束。散射波之间可能存在其他相位关系，但不会导致这种相互加强。另一个极端是图 3.1 b W 中所示的情况，其中散射后的路径长度差是半 w 的某个整数