XiaoMi-AI文件搜索系统
World File Search System量子算法的大统一
与传统算法相比,量子算法在解决各种问题时都具有显著的加速效果。量子搜索、量子相位估计和哈密顿模拟算法是这一优势的最有力论据,这些算法是大量复合量子算法的子程序。最近,许多量子算法通过一种称为量子奇异值变换 (QSVT) 的新技术结合在一起,该技术使人们能够对嵌入酉矩阵的线性算子的奇异值进行多项式变换。在关于 QSVT 的开创性 GSLW'19 论文 [Gilyén et al. , ACM STOC 2019] 中,涵盖了许多算法,包括振幅放大、量子线性系统问题方法和量子模拟。在这里,我们通过这些发展提供了一个教学教程,首先说明了如何将量子信号处理推广到量子特征值变换,QSVT 自然而然地从中产生。与 GSLW'19 并行,我们使用 QSVT 构建直观的量子算法,用于搜索、相位估计和汉密尔顿模拟,并展示特征值阈值问题和矩阵求逆的算法。本概述说明了 QSVT 是如何成为一个包含三种主要量子算法的单一框架的,这表明量子算法实现了大统一。
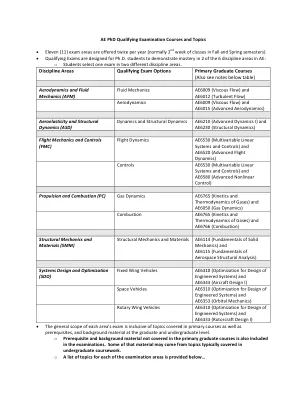
博士考试课程和主题_v3
• 频率响应 • 伯德增益和相位图 控制系统分析和设计 • 传递函数、框图和信号流图 • 稳定性分析、瞬态性能、稳态误差 • 劳斯稳定性标准 • 根轨迹技术 • PI、PD 和 PID 控制器 • 极点和零点对系统响应的影响、极点-零点抵消 控制系统的频域分析和设计 • 伯德增益和相位图 • 增益和相位裕度、相对稳定裕度、稳健性 • 超前和滞后动态补偿 • 奈奎斯特图和奈奎斯特稳定性标准 矩阵数学 • 矩阵分解(Jordan、Schur、奇异值) • 非负定矩阵和正定矩阵 • 矩阵范数、广义逆 • 矩阵指数
h-infinity 输出反馈控制:应用于无人驾驶
5.6 带控制器的环路形状对象................................................................................. 81 5.7 环路增益奇异值图............................................................................................... 82 5.8 湍流模型仿真................................................................................................ 83 5.9 随机速度扰动矢量................................................................................................. 84 5.10 对单位倾斜角阶跃命令的闭环横向状态响应......................................................................... 86 5.11 对单位倾斜角阶跃命令的闭环纵向状态响应......................................................................................... 87 5.12 对单位倾斜角阶跃需求的控制历史............................................................................. 88 5.13 对单位俯仰角阶跃命令的闭环纵向状态响应......................................................................................... 89 5.14 对单位俯仰角阶跃命令的闭环横向状态响应......................................................................................... 90 5.15 对单位俯仰角阶跃需求的控制历史............................................................................. 91 5.16 控制器结构................................................................................
预测性空气和空气动力建模
量子线性求解器是求解方程线性系统的最早且众所周知的量子算法之一是Harrow,Hassidim和Lloyd [8]。这实现了复杂性的指数改善(即运行时)。随后在Childs等人的量子算法中获得了相对于精度的提高复杂性。[9]。这是通过基于量子奇异值转换(QSVT)代替[8]的量子相估计来实现的。Childs等人的算法。可以看作是Gilyen等人的更通用QSVT算法的特殊情况。[10]。应注意的是,由于州准备或状态读数要求,任何潜在的指数改进都处于风险的危险中[11]。这需要以某种形式解决,而无需使用“被动QRAM”,而没有已知的可扩展物理实现[12]。
系统辨识中一般矩阵的量子线性系统算法
摘要:求解线性方程组是经典辨识系统中最常见、最基本的问题之一。给定一个系数矩阵A和一个向量b,最终任务是寻找解x使得Ax=b。基于奇异值估计技术,该文提出一种改进的量子方案,对于一般的m×n维矩阵A,在O(κ2√rpolylog(mn)/ϵ)时间内得到线性方程组解对应的量子态|x⟩,该方案优于现有的量子算法,其中κ为条件数,r为矩阵A的秩,ϵ为精度参数。同时,我们还设计了一个针对齐次线性方程组的量子电路,并取得了指数级的提升。我们方案中的系数矩阵A是与稀疏性无关的非方阵,可以应用于更一般的场合。我们的研究提供了一个通用的量子线性系统求解器,可以丰富量子计算的研究范围。
矩阵补全的更简单方法
本文给出了迄今为止重建未知低秩矩阵所需的随机采样条目数的最佳界限。这些结果改进了 Cand`es 和 Recht (2009)、Cand`es 和 Tao (2009) 以及 Keshavan 等人 (2009) 的先前工作。重建是通过最小化隐藏矩阵的核范数或奇异值之和来实现的,前提是与提供的条目一致。如果底层矩阵满足某种不相干条件,则所需的条目数等于二次对数因子乘以奇异值分解中的参数数。这一断言的证明很短、自成体系,并使用非常基本的分析。本文中的新技术基于量子信息理论的最新研究。关键词:矩阵完成、低秩矩阵、凸优化、核范数最小化、随机矩阵、算子切尔诺夫界限、压缩感知
量子计算解析
解答 54 算子的迹 54 例 3.8 54 解答 54 例 3.9 55 解答 55 迹的重要性质 56 例 3.10 56 解答 56 例 3.11 57 解答 57 算子的期望值 57 例 3.12 57 解答 58 例 3.13 58 解答 59 算子的函数 59 酉变换 60 例 3.14 61 解答 61 投影算子 62 例 3.15 63 解答 63 你试试 63 例 3.16 65 解答 65 正算子 66 交换子代数 66 例 3.17 67 解答 67 海森堡不确定性原理 68 极分解和奇异值 69 例 3.18 69 解答 70 量子力学 70 公设 1:系统的状态 70 公设 2:算符表示的可观测量 70 公设 3:测量 70 公设 4:系统随时间演变 71 练习 71
分布式NASH平衡寻求超过时变的定向通信网络
摘要 - 本文提出了一种分布式算法,以在一类不合作凸的游戏中找到NASH均衡,并具有部分决策信息。我们的方法与共识动态一起采用了分布式的投影梯度播放方法,而单个代理通过梯度步骤和与邻居的本地信息交流通过随时间变化的有向通信网络来最大程度地减少其本地成本。解决时变的定向图提出了重大挑战。现有方法通常通过关注静态图或有向图的特定类型或要求使用Perron-Frobenius EigenVectors进行扩展来避免这种情况。相比之下,我们建立了新的结果,该结果为与时变的行定量重量矩阵相关的混合术语提供了收缩特性。我们的方法根据权重矩阵和图形连接结构的特征明确表示收缩系数,而不是通过先前的研究中的第二大重量矩阵的奇异值隐式表示。既定的结果有助于证明所提出的算法的几何融合,并提高了随着时变的定向通信网络中分布式算法的收敛分析。nash-cournot游戏的数值结果证明了该方法的功效。
优化Kreiss常数
是矩阵非正常行为的定量度量[33,4],这是因为K(a)≥1,例如如果a是正常的。更确切地说,当且仅当M 0(a)= 1达到其全局最小值时,将获得全局最小值k(a)= 1,这是在这些矩阵a a at a at是光谱规范中的收缩。在动态系统的领域之外,例如,k(a)的定量方面在网络分析中引起了人们的关注[4]。尽管我们在这里的主要关注点是矩阵,但值得一提的是C 0 - 操作员半组的情况。这里的左手估计k(a)≤m0(a)从(4)仍然有效,观察到k(a)= 1 = 1表示m 0(a)= 1,在频谱规范中至少在Hilbert Space中获得了Hilbert Space的全局最小值。这两个事实都是Hille-Yoshida定理的简单后果[11]。结论是,即使对于半组,瞬态动力学也可以通过Kreiss常数进行适当评估。虽然Kreiss常数K(A)在许多书籍,文章和文章中受到了广泛的关注,以分析瞬态系统行为的理论数量[33],但最近才解决了其计算。在[24]中,作者与全局搜索同时使用各种本地优化技术来计算具有认证的k(a)。在[33]中,k(a)仅通过绘制比率αϵ(a) /ϵ的比率来估算,并搜索最大值,这似乎是在[23]中开创的。纸张的结构如下。在本文中,我们表明可以使用可靠控制的技术以有限的复杂性来准确地计算kreiss常数k(a)。我们的新特征为更具挑战性的情况开辟了道路,在这种情况下,克里斯常数不仅是构成的,而且更加雄心勃勃,在闭环中最小化,目的是通过使用反馈来限制植物的瞬时生长(1)。简而言之,一个人可能希望使用反馈使闭环A CL更靠近承包瞬态行为,而不是原始矩阵a。这有望在非线性系统的反馈控制中产生后果,众所周知,即使对于良好的抑制抑制型的效应,稳定状态下的雅各布式的非正态性也可能导致较大的瞬态扩增,或者导致非线性效应,或者导致不良极限限制动力学。这种现象在流体动态社区中众所周知[19,28,30,34,26]。在第2节中,我们获得了k(a)的公式,该公式可通过将其与结构化的奇异值或在鲁棒系统分析中知道的结构化奇异值或µ相关联,以合理的效果来计算它。在第3节中,我们扩大了范围,并解决了在闭环中最小化K(A Cl)的问题。由于这是一个NP硬性问题,因此提出了一种快速的启发式,该问题基于非差优化技术。第4节简要概述了这些技术,并显示了如何使用第2节的技术来证明本地优化的结果。数值实验和其他并发技术在第5节中提供。
具有张量网络的隐私机器学习
张量网络广泛用于提供有效的局部量子多体系统的低能状态的有效表示,最近被提议为Ma-Chine学习体系结构,这些体系结构可以在传统方面具有优势。在这项工作中,我们表明,张量网络体系结构尤其具有潜在的潜在属性来保存机器学习,这在诸如医疗记录处理之类的任务中至关重要。首先,我们描述了馈电神经网络中存在的一个新的隐私漏洞,以合成和现实世界数据集进行了说明。然后,我们开发明确定义的条件,以确保对这种脆弱性的鲁棒性,这涉及仪表符号下的模型的表征。我们严格地证明,张量 - 网络构造可以满足此类条件。这样做,我们为基质产品状态定义了一种新型的规范形式,该状态具有高度的规律性,并根据基于奇异值分解的规范形式固定剩余的规格。我们通过在医疗记录数据集中对矩阵产品状态进行培训的实际示例补充发现结果,这表明攻击者从模型的术语中提取有关培训数据集的信息的可能性很大。鉴于在训练张量 - 网络架构方面的专业知识越来越大,这些重新