XiaoMi-AI文件搜索系统
World File Search System签名的图形神经差分方程用于建模连续时间动力学
建模连续时间动力学构成了基础挑战,并且在复杂系统中发现组件相关性具有增强动态建模的效率的希望。具有普通微分方程的Ingrating Graph神经网络的流行方法表现出了有希望的性能。但是,他们无视图表上关键的签名信息潜力,阻碍了他们准确捕获现象的能力并导致了差异。为了回应,我们引入了一种新颖的方法:签名的图形神经顺序差分方程,熟练地解决了误乘签名的信息的局限性。我们提出的解决方案具有灵活性和效率。为了证实其效率,我们将设计的策略无缝地整合到三个杰出的基于图的动态建模框架中:图形神经常规微分方程,图形神经控制的微分方程和图复发的神经网络。严格的评估包括来自物理和生物学的三种动态场景,以及四个真实现实世界流量数据集的审查。的经验结果非常优于基准的三重奏,强调了我们所提出的方法促进的实质性增强。我们的代码可以在https://github.com/beautyonce/sgode上找到。
学习增强的非线性模型预测性控制使用基于知识的神经差分方程和深度
非线性模型预测控制(MPC)是一种灵活且越来越流行的框架,用于合成可以满足状态和控制输入约束的反馈控制策略。在此框架中,在每个时间步骤中都解决了以非线性动力学模型为特征的一组动力学约束的优化问题。尽管具有多功能性,但非线性MPC的性能通常取决于动力学模型的准确性。在这项工作中,我们利用深度学习工具,即基于知识的神经普通微分方程(KNODE)和深层合奏,以提高该模型的预测准确性。特别是,我们学到了一个Knode模型的集合,我们将其称为Knode集合,以获得对真系统动力学的准确预测。然后将这个学到的模型集成到一种新颖的学习增强的非线性MPC框架中。我们提供了足够的条件,可以保证闭环系统的渐近稳定性,并表明这些条件可以在实践中实施。我们表明,knode集成提供了更准确的预测,并使用两个案例研究说明了所提出的非线性MPC框架的效率和闭环性能。关键字:非线性模型预测性控制,深度学习,神经差异方程,深层合奏
覆盖示例 - 奥马尔·阿卜杜拉(Omar Abdallah)
斯坦福大学2027年6月 与计算机科学机械工程学的当前GPA:4.0/4.0课程(包括2024年秋季):热力学,动力学,力学,力学,电力和磁性,光与热,光与热,线性代数和多变量计算,用于工程师的普通差分方程斯坦福大学2027年6月与计算机科学机械工程学的当前GPA:4.0/4.0课程(包括2024年秋季):热力学,动力学,力学,力学,电力和磁性,光与热,光与热,线性代数和多变量计算,用于工程师的普通差分方程
CSC 2541:图像的生成AI
(例如,CSC 413/2516)•对神经网和CNN的坚实熟悉•线性代数的固体背景•多元计算和概率•差分方程将有用•编程技能(例如,Tensorflow或Pytorch,如果
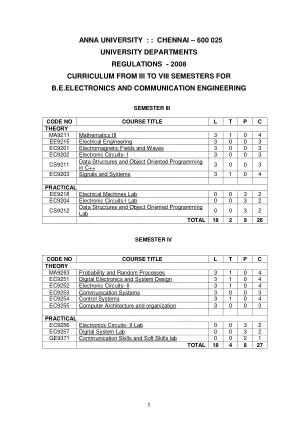
ECE III TO VIII.pdf - 学术课程中心
傅里叶积分定理 – 傅里叶变换对-正弦和余弦变换 – 性质 – 基本函数变换 – 卷积定理 – 帕塞瓦尔恒等式。第三单元偏微分方程 9+3 形成 – 一阶方程的解 – 标准类型和可简化为标准类型的方程 – 奇异解 – 拉格朗日线性方程 – 通过给定曲线的积分曲面 – 具有常数系数的高阶线性方程的解。第四单元偏微分方程的应用 9+3 变量分离法 – 一维波动方程和一维热方程的解 – 二维热方程的稳态解 – 笛卡尔坐标中的傅里叶级数解。第六单元 Z – 变换和差分方程 9+3 Z 变换 – 基本性质 – 逆 Z 变换 – 卷积定理 – 初值和终值定理 – 差分方程的形成 – 使用 Z 变换求解差分方程。L:45,T:15,总计:60 节课 教科书 1.Grewal,B.S.“高等工程数学”,Khanna Publications(2007) 参考文献 1.Glyn James,“高级现代工程数学”,Pearson Education(2007) 2.Ramana,B.V. “高等工程数学”Tata McGraw Hill(2007)。3.Bali, N.P.和 Manish Goyal,“工程教科书第 7 版 (2007) Lakshmi Publications (P) Limited,新德里。
遗传调节系统的建模和模拟
为了理解生物在分子水平上的功能,我们需要知道表达哪些基因,何时何地在生物体中以及在哪个程度上。通过DNA,RNA,蛋白质和小分子之间的相互作用网络所结构的遗传调节系统来实现基因表达的调节。由于大多数遗传调节网络涉及通过互锁正面和负反馈回路相关的许多组件,因此很难获得对其染色体的直观理解。因此,对于遗传调节网络进行建模和模拟的形式方法和计算机工具是必不可少的。本文回顾了数学生物学和生物信息学用于描述遗传调节系统的形式主义,特别是有向图,贝叶斯网络,布尔网络及其概括,普通和部分差分方程,定性微分方程,定性差分方程,随机方程以及基于规则的形式主义。在适当的情况下,本文讨论了如何将这些形式主义用于模拟实际监管系统的行为。
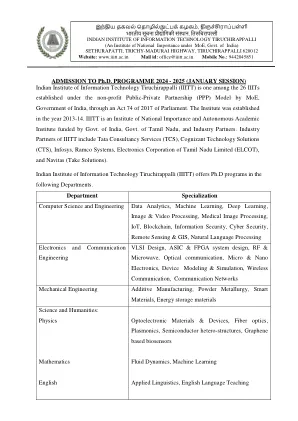
入学博士学位。程序2024-2025(...入学博士学位。程序2024-2025(...
普通微分方程:一阶普通微分方程,初始值问题的存在和唯一性定理,具有恒定系数的高阶的线性普通微分方程;二阶线性差分方程,具有可变系数; Cauchy-euler方程,拉普拉斯的方法转换用于求解普通微分方程,串联解决方案(功率系列,Frobenius方法); Legendre和Bessel功能及其正交特性;线性一阶普通微分方程的系统,Sturm的振荡和分离定理,Sturm-Liouville特征值问题,普通微分方程的平面自主系统:具有恒定系数的线性系统的固定点的稳定性,线性稳定性,线性稳定性,Lyapunov功能。
2024-2025 年学习课程
APL101 工程应用中的应用数学 3 学分 (3-0-0) 常微分方程:二阶 ODE、待定系数法、参数变异、Strum-Liouville 特征值问题、差分方程。偏微分方程:PDE 的分类、热、波和拉普拉斯方程、分离变量以解决 PDE。傅里叶变换:傅里叶正弦变换、傅里叶余弦变换、解决 ODE 和 PDE 的技术。概率论:概率公理、条件概率、随机变量、工程系统中的不确定性、离散和连续分布、分布函数、联合概率分布、矩、协方差、相关系数。随机过程:随机过程的定义、随机 FE 模型、平稳过程、马尔可夫链、泊松过程。
基于机动车尾气扩散引起的二氧化氮大气污染过程间隔数据分析的建模
摘要:本文讨论了考虑汽车尾气对大气表面层二氧化氮污染的建模问题。提出了区间数据分析方法。首次提出并建立了基于已知测量误差的数据分析来识别大气污染物二氧化氮分布数学模型的方法。所获得的差分方程形式的数学模型的特点是可以保证准确预测城市特定区域的二氧化氮浓度。它还充分考虑了交通变化,从而大大降低了环境控制和监测成本。与已知方法相比,所提出的新模型识别方法在计算时间复杂度方面更有效,并且它基于对测量误差的考虑,这在最终情况下提供了具有保证准确性的模型预测特性。
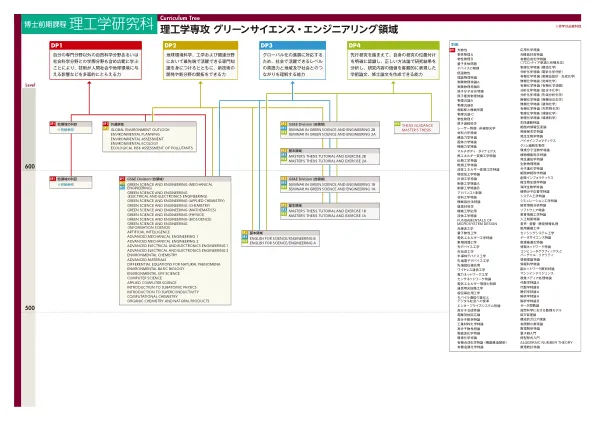
绿色科学与工程部,绿色科学工程领域
GREEN SCIENCE AND ENGINEERING(MECHANICAL ENGINEERING) GREEN SCIENCE AND ENGINEERING (ELECTRICAL AND ELECTRONICS ENGINEERING) GREEN SCIENCE AND ENGINEERING(APPLIED CHEMISTRY) GREEN SCIENCE AND ENGINEERING(CHEMISTRY) GREEN SCIENCE AND ENGINEERING(MATHEMATICS) GREEN SCIENCE AND ENGINEERING(PHYSICS) GREEN SCIENCE AND ENGINEERING(BIOSCIENCE) GREEN SCIENCE AND ENGINEERING (INFORMATION SCIENCE) ARTIFICIAL INTELLIGENCE ADVANCED MECHANICAL ENGINEERING 1 ADVANCED MECHANICAL工程2高级电气和电子工程1高级电气和电子工程2环境化学的自然现象的高级材料差分方程环境基本生物学环境环境科学计算机科学应用计算机科学介绍超导性计算计算计算计算化学化学和天然产品