XiaoMi-AI文件搜索系统
World File Search System硅芯CX1084微电子5A低压差...
CX1084 系列可调和固定电压调节器旨在提供 5A 输出电流,输入输出差压低至 1V。器件的压差在最大输出电流时保证最大为 1.5V,在较低负载电流时降低。片上微调可将参考电压调整至 1%。电流限制也经过微调,最大限度地减少过载条件下调节器和电源电路的应力。CX1084 器件与较旧的三端调节器引脚兼容,采用 3 引线 TO-220、2 引线 TO-252 封装以及 3 和 2 引线 TO-263(塑料 DD)封装。
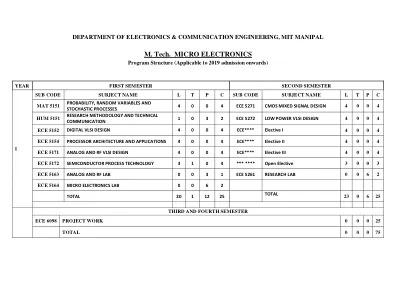
M. Tech。微电子 b''
co1应用与统计推断有关的概念,例如随机抽样和采样分布。CO2根据样本估算分布的参数,并进行假设检验,回归分析,相关性和方差分析。 CO3应用数学和统计数据的全面知识来解决静态概率,动态概率的问题。 CO4使用随机过程的知识,提出现实生活中的问题并确定长期概率。 co5基于毒物过程,估计排队系统统计推断的各种性能度量:随机抽样,抽样分布,参数估计和假设检验,回归,相关性和方差的相关性和分析 - 示例 - 示例。 静态概率,动态概率。 状态分类,马尔可夫过程的链。 马尔可夫系统的稳定性,限制行为,随机步行。 泊松过程:假设和衍生,相关分布,出生和死亡过程。 排队系统,一般概念,M/M/1模型和M/M/S,稳态行为,瞬态行为。 参考:1。 Hogg&Craig(1975),“数学统计概论”,第4THEDN。,MACMILLAN,2。 J.Medhi,“随机过程”。 3。 A. Papoulis和S.U. Pillai,概率,随机变量和随机过程,CO2根据样本估算分布的参数,并进行假设检验,回归分析,相关性和方差分析。CO3应用数学和统计数据的全面知识来解决静态概率,动态概率的问题。CO4使用随机过程的知识,提出现实生活中的问题并确定长期概率。co5基于毒物过程,估计排队系统统计推断的各种性能度量:随机抽样,抽样分布,参数估计和假设检验,回归,相关性和方差的相关性和分析 - 示例 - 示例。静态概率,动态概率。状态分类,马尔可夫过程的链。马尔可夫系统的稳定性,限制行为,随机步行。泊松过程:假设和衍生,相关分布,出生和死亡过程。排队系统,一般概念,M/M/1模型和M/M/S,稳态行为,瞬态行为。参考:1。Hogg&Craig(1975),“数学统计概论”,第4THEDN。,MACMILLAN,2。 J.Medhi,“随机过程”。 3。 A. Papoulis和S.U. Pillai,概率,随机变量和随机过程,Hogg&Craig(1975),“数学统计概论”,第4THEDN。,MACMILLAN,2。J.Medhi,“随机过程”。3。A. Papoulis和S.U. Pillai,概率,随机变量和随机过程,A. Papoulis和S.U.Pillai,概率,随机变量和随机过程,
微电子技能和职业概况
在数字化时代,微电子技术日益渗透到我们的日常生活和工作环境中。微电子芯片不仅存在于智能手机、笔记本电脑和办公电脑中,它们还可以调节我们的电源、控制移动互联网的数据流,并实现安全互联的自动化移动。微电子处理器也是人工智能的大脑。在医疗保健和工业制造等领域,微电子技术可确保服务和产品满足最高的功能和质量标准。这使得微电子技术成为数字化时代繁荣的重要基础:通过提供改善生活质量的服务并确保可持续的价值创造和就业。
EE 252 微电子器件和电路教学大纲...
只有当你有正当理由缺席考试(比如生病、家人去世、交通事故等)时,才可以补考期中考试 1 和 2。如遇生病或紧急情况,你必须提供支持性正式文件。另外需要注意的是,补考将以期末考试的形式进行,涵盖所有科目。 III. 延迟提交政策 延迟提交的试卷将不予评分。小测验和家庭作业/作业不予补考。错过作业和小测验将导致成绩为零 (0)。 IV. 参与 在他们的《成人学生生存与成功指南》一书中,Al Siebert 和 Mary Karr 建议最有效的学习方法是通过提问和回答问题来学习。养成阅读教科书、做笔记和通过提问和回答问题学习的习惯。当你这样做时,你可以节省很多学习时间,并有时间与家人或朋友共度。提出和回答问题有多种方法。
微电子行业的安全与健康指南-DTIC
摘要微电子行业在全国范围内雇用约18万名工人。在半导体组件和集成电路的制造中使用了约95,000个;大约有60,000名用于电容器,电阻和冷凝器的生产;余额生产其他电子产品。这个高科技行业的流行印象是,穿着白色西服的员工在干净,明亮的工作场所穿着白色西装。尽管在许多情况下是准确的,但该行业中的许多高科技工人风险可能会暴露于各种各样的危险物质。科学研究已经确定了该行业内部的许多危险状况和最高的职业疾病率。
微电子和分布式能源的硅电沉积:简要回顾
摘要:由于硅在自然界的普遍性和其特殊的性质,它是各行各业中最受欢迎的材料之一。目前,冶金硅是通过石英的碳热还原获得的,然后对其进行氢氯化和多重氯化以获得太阳能硅。这篇小型综述简要分析了通过电解熔盐获得硅的替代方法。综述涵盖了决定熔盐成分选择的因素、通过电解熔盐获得的典型硅沉淀物、对将电解硅用于微电子的可能性的评估、在锂离子电流源成分中使用电解硅的代表性测试结果以及将电解硅用于太阳能转换的代表性测试结果。本文最后指出了实际实施电解生产硅的方法、开发用于能源分配和微电子应用的新设备和材料需要解决的任务。
上海复旦微电子集团股份有限公司
研究开发、生产、销售通讯产品、移动通信终端产品、高新技 术产品,并提供相关服务,从事集成电路技术领域内的技术开 发、技术咨询、技术服务、技术转让,微电子产品及金属材料 的销售,卫星地面接收设施安装。 【依法须经批准的项目,经 相关部门批准后方可开展经营活动】
上海复旦微电子集团股份有限公司
海外监管公告本公告乃上海复旦微电子集团股份有限公司(「本公司」)根据香港联合交易所有限公司证券上市规则第13.10B 条的规定刊发。 兹载列本公司于上海证券交易所网站刊发的《关于股东所持部分股份被司法处置的进展公告》,仅供参阅。