XiaoMi-AI文件搜索系统
World File Search System使用 qBang 优化变分量子算法
变分量子算法 (VQA) 代表了一种利用当前量子计算基础设施的有前途的方法。VQA 基于通过经典算法在闭环中优化的参数化量子电路。这种混合方法减少了量子处理单元的负载,但代价是经典优化会产生平坦的能量景观。现有的优化技术,包括虚时间传播、自然梯度或基于动量的方法,都是有前途的候选方法,但要么给量子设备带来沉重的负担,要么经常遭受收敛速度缓慢的困扰。在这项工作中,我们提出了量子 Broyden 自适应自然梯度 (qBang) 方法,这是一种新颖的优化器,旨在提炼现有方法的最佳方面。通过采用 Broyden 方法近似 Fisher 信息矩阵中的更新并将其与基于动量的算法相结合,qBang 降低了量子资源需求,同时比资源要求更高的替代方案表现更好。荒原、量子化学和最大切割问题的基准测试表明,在以下情况下,其整体性能稳定,并且比现有技术有明显改进
BRAINGPT:一个受大脑启发的基于 SNN 的大型
基于人工神经网络 (ANN) 的大型语言模型 (LLM) 表现出色,但在计算效率和生物可解释性方面面临挑战。我们提出了 BrainGPT,这是一种基于测试时间训练 (TTT) 框架并受到脉冲神经网络 (SNN) 和神经生物学原理启发的新型 LLM 架构。我们的方法采用双模型结构,模拟人脑中观察到的分层语言处理,并利用具有自适应阈值的专门积分和激发神经元模型。通过多阶段训练策略,包括量化感知预训练、ANN 到 SNN 的转换和受生物启发的无监督学习,我们实现了从 ANN 到 SNN 的数学证明的无损转换,保留了 100% 的原始 ANN 模型的性能。此外,受生物启发的无监督学习优化了维持 100% ANN 性能所需的最大时间步骤。与原始 TTT 模型相比,BrainGPT 的能源效率提高了 33.4%,训练收敛速度提高了 66.7%。这项工作推动了节能且可生物解释的大型语言模型的开发,这些模型的性能可与最先进的基于 ANN 的模型相媲美,同时显著改进了 TTT 框架。
通过多代理深钢筋学习在航空等级边缘计算系统中的计算卸载
摘要 - 物联网(IoT)设备和新兴应用程序的指数增长显着提高了对无处不在的连通性和有效计算范式的要求。传统的地面边缘计算体系结构无法在全球范围内提供庞大的物联网连接。在本文中,我们提出了一个由高空平台(HAP)和无人机(无人机)组成的航空层级移动边缘计算系统。特别是,我们考虑了不可分割的任务,并制定了流动问题的任务,以最大程度地降低任务的长期处理成本,同时满足流量的过程和任务处理过程中的排队机制。我们提出了基于多代理的深钢筋学习(DRL)的流量算法计算,其中每个设备可以根据局部观察结果做出其流量决策。由于无人机的计算资源有限,无人机的高任务负载将增加放弃流量任务的比率。为了增加完成任务的成功率,使用卷积LSTM(Convlstm)网络来估计无人机的未来任务负载。此外,提出了优先的体验重播(PER)方法以提高收敛速度并提高训练稳定性。实验结果表明,所提出的流量算法的计算优于其他基准方法。
自主停车的TD3中损失函数的比较分析
自主停车是一种革命性的技术,它随着深度强化学习的兴起,尤其是双胞胎延迟的深层确定性政策梯度算法(TD3),它改变了汽车行业。尽管如此,由于Q值估计的偏见,在确定在特定状态下采取的行动的良好时,TD3的鲁棒性仍然是一个重大挑战。为了研究这一差距,本文分析了TD3中的不同损失函数,以更好地近似真正的Q值,这对于最佳决策是必不可少的。评估了三个损失功能;平均平方错误(MSE),平均绝对误差(MAE)和HUBER损失,通过模拟实验进行自动停车。结果表明,HUBER损失的TD3具有最高的收敛速度,而最快的演员和批评损失收敛。发现Huber损失函数比孤立使用的MSE或MAE这样的损耗函数更强大,更有效,这使其成为TD3算法中现有损失函数的合适替代。将来,当估计的Q值代表以特定状态采取行动的预期奖励的估计Q值时,将使用Huber损失的TD3用作解决TD3中高估问题的基本模型。
填补空白:探索生成式人工智能以增强异构移动边缘设备的联邦学习
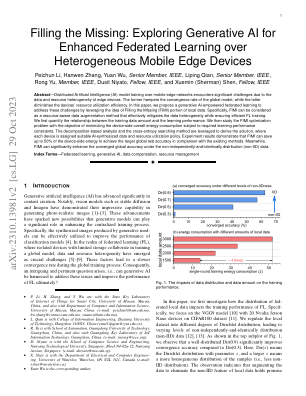
摘要 — 由于边缘设备的数据和资源异构性,在移动边缘网络上进行分布式人工智能 (AI) 模型训练面临重大挑战。前者阻碍了全局模型的收敛速度,而后者降低了设备的资源利用效率。在本文中,我们提出了一种生成式 AI 赋能的联邦学习来应对这些挑战,它利用了填充本地数据缺失部分 (FIMI) 的思想。具体而言,FIMI 可以被视为一种资源感知的数据增强方法,可在确保高效的 FL 训练的同时有效缓解数据异构性。我们首先量化训练数据量和学习性能之间的关系。然后,我们研究 FIMI 优化问题,目标是在所需学习性能约束下最小化设备端总体能耗。利用基于分解的分析和交叉熵搜索方法得出解决方案,其中为每个设备分配合适的 AI 合成数据和资源利用策略。实验结果表明,与现有方法相比,FIMI 可以节省高达 50% 的设备端能量,以达到目标全局测试精度。同时,FIMI 可以显著提高非独立同分布 (non-IID) 数据下的收敛全局精度。
大数据选项远离障碍物跟踪
摘要 - 我们的研究在多代理网络中分发了大数据非convex优化。我们考虑平滑(可能)非凸功能的总和的(受约束的)最小化,即代理的总和,以及凸(可能)的凸(可能)非平滑正常器。我们的兴趣是大数据问题,其中有大量变量需要优化。如果通过标准分布式优化算法进行处理,则这些大规模问题可能会因为每个节点的局部计算和通信负担过高,因此可能会棘手。我们提出了一种新颖的分布式解决方案方法,在每种迭代中,代理以不协调的方式更新整个决策向量的一个块。为了处理成本函数的非概念性,新型方案取决于连续的凸近似(SCA)技术,结合了一种新颖的块驱动的推动力共识方案,该方案对执行局部扩展的块状操作和梯度平均跟踪非常有用。建立了渐近收敛到非凸问题的固定溶液。最后,数值结果显示了提出的算法的有效性,并突出了块维度如何影响通信开销和实际收敛速度。
智能家居的可迁移强化学习
为了充分利用需求侧大量未开发的资源,智能家居技术在解决智能电网“最后一英里”问题中发挥着至关重要的作用。强化学习 (RL) 在解决许多连续决策问题方面表现出色,是智能家居控制的绝佳候选。例如,许多研究已经开始研究动态定价方案下的家电调度问题。基于这些,本研究旨在提供一种经济实惠的解决方案,以鼓励更高的智能家居采用率。具体来说,我们研究将迁移学习 (TL) 与 RL 相结合,以降低最佳 RL 控制策略的训练成本。给定基准住宅的最佳策略,TL 可以启动针对具有不同家电和用户偏好的新住宅的策略的 RL 训练。模拟结果表明,通过利用 TL,RL 训练收敛速度更快,并且对于与基准住宅相似的新住宅,所需的计算时间要少得多。总之,本研究提出了一种经济有效的方法来大规模训练家庭 RL 控制策略,最终降低控制器的实施成本,提高 RL 控制器的采用率,并使更多家庭实现电网互动。
FedZero:在联邦学习中利用可再生过剩能源
联邦学习 (FL) 是一种新兴的机器学习技术,它支持跨数据孤岛或边缘设备进行分布式模型训练,而无需数据共享。然而,与集中式模型训练相比,FL 不可避免地会带来效率低下的问题,这将进一步增加未来机器学习本已很高的能耗和相关的碳排放。减少 FL 碳足迹的一种方法是根据电网中特定时间和地点可能出现的可再生过剩能源的可用性来安排训练作业。然而,面对如此不稳定且不可靠的资源,现有的 FL 调度程序无法始终确保快速、高效和公平的训练。我们提出了 FedZero,这是一个专门依靠可再生过剩能源和计算基础设施的闲置容量运行的 FL 系统,可有效地将训练的运营碳排放量降至零。通过利用能源和负荷预测,FedZero 通过选择客户端实现快速收敛和公平参与,从而利用过剩资源的时空可用性。我们基于实际的太阳和负载轨迹进行的评估表明,在上述约束条件下,FedZero 的收敛速度明显快于现有方法,同时消耗的能量更少。此外,它对预测误差具有很强的鲁棒性,可扩展到数万个客户端。
全脑放射组学在脑肿瘤分割中的聚类联合个性化
联邦学习及其在医学图像分割中的应用最近已成为一个热门的研究课题。这种训练范式存在参与机构本地数据集之间的统计异质性问题,与传统训练相比,会导致收敛速度减慢以及潜在的准确性损失。为了减轻这种影响,联邦个性化应运而生,即每个机构一个模型的联邦优化。我们提出了一种新颖的个性化算法,该算法针对不同机构使用不同扫描仪和采集参数引起的特征变化而量身定制。该方法是第一个考虑机构间和机构内特征变化(单个机构使用多台扫描仪)的方法。它基于在每个中心内计算一系列放射组学特征,捕捉每个 3D 图像体积的整体纹理,然后进行聚类分析,将所有特征向量从本地机构传输到中央服务器。然后,每个计算出的聚类分散数据集(可能包括来自不同机构的数据)用于微调通过经典联邦学习获得的全局模型。我们在联邦脑肿瘤分割 2022 挑战数据集 (FeTS2022) 上验证了我们的方法。我们的代码可在 (https://github.com/MatthisManthe/radiomics_CFFL) 上找到。关键词:联邦学习、联邦个性化、分割、脑肿瘤分割。
使用新型 Bonobo 优化器对离网混合可再生能源系统进行技术和经济评估
摘要:本研究采用一种新颖的 bonobo 优化器 (BO) 技术来寻找离网混合可再生能源系统 (HRES) 的最佳设计,该系统包含柴油发电机、光伏 (PV)、风力涡轮机 (WT) 和电池作为存储系统。拟议的 HRES 旨在为沙特阿拉伯北部偏远地区提供电力,其基础是年度系统成本 (ASC) 最小化和电力系统可靠性增强。为了区分和评估性能,将 BO 与四种最近的元启发式算法进行了比较,这四种算法称为大爆炸大收缩 (BBBC)、乌鸦搜索 (CS)、遗传算法 (GA) 和蝴蝶优化算法 (BOA),以根据捕获的最优和最差解决方案、平均值、收敛速度和标准差为拟议的离网 HRES 找到最佳设计。所得结果显示,与其他四种元启发式算法相比,BO 算法更为有效,它以最低的 ASC(149,977.2 美元)、快速的收敛时间和更少的振荡实现了所提出的离网 HRES 的最优解,其次是 BOA(150,236.4 美元)。BBBC 和 GA 算法都无法捕捉到全局解,并且收敛时间较长。此外,它们具有较高的标准差,这表明它们的解决方案更加分散,振荡明显。这些模拟结果证明了与其他四种元启发式算法相比,BO 算法的优势。