XiaoMi-AI文件搜索系统
World File Search System数学方法
物理学的数学方法
o 获得持续学习和知识更新的基本知识工具 o 学生将培养不断更新物理研究中的数学技术和技能的态度。 教学大纲 内容知识 度量空间。定义。例子。开集、闭集、邻域。拓扑空间。连续映射。稠密集、可分空间。收敛和柯西序列。完备性。例子。度量空间的完备性。巴拿赫空间。向量空间。范数空间。完备性和巴拿赫空间。例子：有限维空间、序列空间、函数空间。有界线性算子。连续性和有界性。BLT 定理。连续线性泛函和对偶空间。有界线性算子的巴拿赫空间。例子。测度论简介。勒贝格积分。Sigma 代数和 Borel 测度。可测函数。支配和单调收敛。富比尼定理。例子：绝对连续测度、狄拉克测度、康托测度。勒贝格分解定理。希尔伯特空间。内积。欧几里得空间和希尔伯特空间。正交性、勾股定理。贝塞尔不等式和柯西-施瓦茨不等式。三角不等式。平行四边形定律和极化恒等式。例子。直和。投影定理。Riesz-Fréchet 引理。正交系统和傅里叶系数。正交基和 Parseval 关系。Gram-Schmidt 正交化程序。与 l^2 同构。张量积和积基。希尔伯特空间上的线性算子。有界算子的 C ∗ -代数。正规、自伴、酉和投影算子。Baire 范畴定理。一致有界性原理。一致、强和弱收敛。一些量子力学。无界算子。伴生。对称和自伴算子。例子：乘法和导数算子。本质自伴算子。自伴性和本质自伴性的基本标准。图、闭包
针对不确定的可再生能源生产时间表问题的稳健修复和优化数学方法
摘要 — 本研究提出了一种修复和优化数学方法来解决不确定情况下的时间表问题。具体来说，考虑一个大学时间表和电力存储调度问题，受可再生能源生产和电力需求不确定性的影响。该问题被表述为一个大型混合整数规划 (MIP)，所提出的解决方案结合了大邻域搜索和基于场景的稳健优化，以处理目标函数中的不确定性。首先，仅考虑硬问题约束（在本例中为重复讲座活动的安排）即可得出一个足够可行的时间表。接下来，通过修复和优化启发式搜索改进解决方案。在每次迭代中，MIP 求解器通过修复变量子集并对剩余的自由变量进行优化来探索一个大邻域。该过程重复多次，直到满足停止标准。为了解决目标中的不确定性，从区间预测中得出概率场景，并将最坏情况的能源成本最小化。参与技术挑战的结果表明，所提出的方法能够相对快速地提供具有竞争力的解决方案，即使对于大型问题实例也是如此，同时还可以避免较大的预测误差。索引词 — 修复和优化、局部邻域搜索、可再生能源预测、稳健优化、大学时间表。
1.复杂控制系统的数学方法...
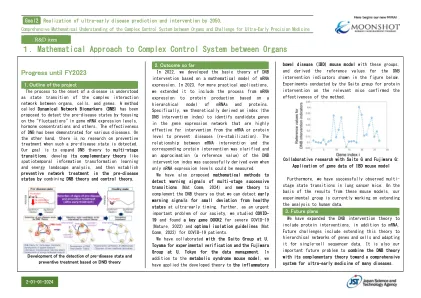
疾病发作的过程被理解为器官，细胞和基因之间复杂相互作用网络的状态转变。已经提出了一种称为动力网络生物标志物（DNB）的方法，以通过重点关注基因mRNA表达水平，激素浓度等中的“波动”来检测前酶疾病。已经证明了DNB的有效性。另一方面，当检测到这种前疾病状态时，没有关于预防性治疗的研究。我们的目标是将DNB理论扩展到多阶段过渡，开发其互补理论，例如时空信息转换学习和能量景观分析，然后通过结合DNB理论和控制理论在疾病前状态中建立预防网络处理。
使用数学方法的供应链与全球通货膨胀之间的关系
“人工智能（AI）是计算机科学，数学和认知心理学交集的变革性领域。它涉及能够执行通常需要人类智能的任务的系统，例如学习，解决问题，感知和决策。AI技术，包括机器学习，自然语言处理和机器人技术，正在彻底改变行业，从医疗保健到金融，并重塑我们的生活方式，工作和与技术互动的方式。”在21世纪，人工智能（AI）已成为一种变革力量，重塑了社会和工业的各个方面。随着计算能力，数据可用性和算法技术方面的进步，AI在使机器能够执行传统上需要人类智能的任务方面取得了长足的进步。
古代计算工具的纯数学方法
摘要：算盘是当今仍在使用的最古老的计算工具之一。基于珠子的接口，尽管它具有简单性，但允许用户通过沿电线或杆的滑动珠系统进行复杂的数学操作。虽然物理算盘本身提供了一种直观的视觉方法来计算，但基本操作依赖于基本的数学原理。本文提供了一个全面的数学框架，该框架正式描述了算盘计算背后的算法。从基本的算盘构型开始，我们定义了建模算盘状态所需的关键组件，例如杆，珠子和珠子值。然后，我们通过集合表示法，复发关系和状态过渡图来表征加法，减法，乘法和除法的核心算法算法。我们形式化的算法算法利用数字理论，模块化算术，组合和代数来利用概念。除了对古代技术提供新的数学见解外，我们的工作还有助于桥接有形的算盘界面与为其供电的抽象算法之间的连接。通过示例和证明，我们展示了珠子操作如何精确地对应于数学转换。这种形式化的水平不仅有助于解释算盘的有效性，而且还说明了即使是基本的计算工具如何利用深刻的数学思想。我们的数学算盘框架为进一步分析以及经典算盘方法的修改和扩展奠定了基础。
从土壤微生物产生淀粉酶-IJRPR 人工光合作用：可再生能源的来源-IJRPR 人工智能半导体技术与发展评论 生物乳化剂生产生物体降解和芳族化合物的分离 使用CAD/CAM技术实现牙齿修复的准确性和精度 纳米技术的肺癌治疗的发展 使用数学方法的供应链与全球通货膨胀之间的关系 人工智能和特定的瑜伽体式及其与人类社会的相关性 航空航天行业中物联网（IoT）的应用 基于物联网的远程和监视太阳能-IJRPR 大脑计算机接口-IJRPR 牙科材料的新兴趋势-IJRPR 关于讲座与小册子对适当伤口护理的知识和实践的影响的比较研究 使用深度学习算法的野生动物检测-IJRPR Rabindranath Tagore的教育理念-IJRPR
酶在各个行业中起关键作用，从食品和饮料到药品和生物燃料。在各种酶中，淀粉酶由于能够将淀粉水解（一种复杂的多糖）催化为较简单的糖而具有重要意义。近年来，对淀粉酶的需求急剧激增，从而广泛研究其生产的微生物来源（Adrio等人。2014）。虽然已经探索了几种生物作为淀粉酶合成的潜在宿主，但土壤生态系统却是淀粉酶产生的微生物的有趣且丰富的储层。酶是在广泛的生物过程中起关键作用的生物催化剂。它们以显着的效率和特异性催化特定的化学反应的能力使它们在各种工业应用中无价。在各种酶阵列中，淀粉酶由于它们能够将淀粉（一种复杂的多糖）水解到诸如葡萄糖和麦芽糖等较简单的糖（Struck等2012）。淀粉酶在诸如食品和饮料，纺织品，纸张和纸浆，洗涤剂，药品和生物燃料生产等行业中发现了广泛使用。对淀粉酶的需求不断增长以及对可持续和生态友好的生产方法的需求导致探索了淀粉酶生产的各种微生物来源（Patel等人2023）。
物理数学方法
UNIT-IV 近似方法非简并和简并能级的时间无关微扰理论 - 应用于谐振子基态和氢的斯塔克效应。 参考文献： 1. 量子力学导论，David J. Griffiths，Pearson（2005）。 2. 量子力学，G. Aruldhas，PHI，印度。 3. 量子力学：概念与应用，N. Zettili，Wiley 4.量子力学，LI Schiff，Tata Mcgraw Hill Education Private Limited Tata Mcgraw Hill Education Private Limited（2010）。 5. 现代量子力学，J. J Sakurai，Pearson（1994）。 6. 量子力学：理论与应用，A. Ghatak，Macmillan India Limited（2004）。 7. 量子力学：导论，Walter Greiner 编，Springer (India) Pvt. Ltd. (2008) 8. 量子物理学：原子、分子、固体、原子核及实践，Robert Resnick 和 Robert Eisberg 编，Wiley India Pvt Ltd (2006)。
用数学方法探索早期纵向动力学
我们系统地研究了流体动力学模拟中超子全局极化对碰撞系统初始纵向流速的敏感性。通过在将初始碰撞几何映射到宏观流体动力学场时明确施加局部能量动量守恒，我们研究了系统的轨道角动量 (OAM) 和流体涡度的演变。我们发现同时描述 Λ 超子的全局极化和介子定向流的斜率可以强烈限制流体动力学演化开始时纵向流的大小。我们利用 RHIC 光束能量扫描程序中的 STAR 测量结果提取了初始纵向流的大小和产生的 QGP 流体中轨道角动量分数作为碰撞能量的函数。我们发现在流体动力学演化开始时，中快速度流体中剩余约 100-200 ℏ OAM。我们进一步考察了不同的流体动力学梯度对Λ和¯ Λ自旋极化的影响。µ B /T的梯度可以改变Λ和¯ Λ极化之间的有序性。
CHEN E4010 化学工程中的数学方法
欢迎！CHEN E4010 化学工程中的数学方法是一门严谨的课程，是化学工程研究生教育基础的重要组成部分。我喜欢数学，因为它与生俱来的美丽，以及在解决几乎所有领域的实际问题方面所具有的强大力量。在本课程中，您将有机会在化学工程问题的背景下欣赏数学。1. CHEN E4010 化学工程中的数学方法 - 3.0 分 先决条件：CHEN E3120 和 E4230，或同等学历，或获得讲师许可。化学工程问题的数学描述以及所选方法在解决方案中的应用。一般建模原理，包括模型层次结构。线性和非线性常微分方程及其系统，包括具有可变系数的系统。用于解决化学工程问题的笛卡尔和曲线坐标中的偏微分方程。 (http://www.columbia.edu/cu/bulletin/uwb/ ) 2. 讲师：Venkat Venkatasubramanian 教授 Mudd 819 212-854-4453，venkat@columbia.edu 教学助理 Jagan Mohan Sanghishetty 先生 电子邮件：js5521@columbia.edu 3. 上课时间/办公时间：a. 上课时间：周二和周四 - 上午 10:10 - 上午 11:25 b. 办公时间：周四下午 4 - 5 点在 Mudd 233。否则需预约。电子邮件联系是方便记录信息的首选联系方式。c. 助教办公时间：待定 4. 教室：Mudd 233 5. 教科书和材料（必需和补充）：