XiaoMi-AI文件搜索系统
World File Search System数学
计算化学中的数学挑战
在过去的二十年中，理论和建模已成为应用化学以及分析化学、合成化学和其他化学领域的主要研究课题之一。这是由于方法论、数值方法以及计算机软件和硬件的重大改进而成为可能的。许多实验研究开始包括计算建模。计算机模拟在现代化学中的作用不可低估，有效的建模和模拟在实际应用中起着至关重要的作用，因为它可以提供对实验的见解并帮助优化系统。具体而言，模拟越来越多地被用来用计算代替危险且昂贵的实验。同时，现代材料科学和生物学实验研究的令人瞩目的进步要求进一步发展和不断扩展当今计算化学方法的适用性和准确性。对大型生物分子、纳米粒子和界面进行快速而准确的定性和定量建模成为研究的主要焦点，这需要大量的计算工作，而且在目前的技术水平下并不总是能够实现。大多数计算化学问题都是关于求解分子中电子的薛定谔方程或经典粒子系统的牛顿运动方程。因此，数学应该在新的发展中发挥核心作用。本次研讨会的主要目的是根据顶尖科学家提供的经验分析计算化学的当前需求和期望，并与方法和计算软件开发人员进行讨论。以下部分以研讨会会议为名，包括初始演讲中提出的主题以及圆桌讨论和人际谈话中提出的主题。
![文章标题：抗击 COVID-19：人工智能技术与挑战 作者：Nikhil Patel[1]、Sandeep Trivedi[2]、Jyotir Moy Chatterjee[3] 所属机构：毕业于杜比克大学，联系电子邮件 ID：Patelnikhilr88@gmail.com[1]，IEEE 会员，毕业于 Technocrats Institute of Technology，联系电子邮件 ID：sandeep.trived.ieee@gmail.com[2]，尼泊尔加德满都佛陀教育基金会[3] Orcid id：0000-0001-6221-3843[1]、0000-0002-1709-247X[2]、0000-0003-2527-916X[3] 联系电子邮件：sandeep.trived.ieee@gmail.com 许可信息：本作品已以开放获取形式发表根据 Creative Commons 署名许可 http://creativecommons.org/licenses/by/4.0/，允许在任何媒体中不受限制地使用、分发和复制，前提是正确引用原始作品。条件、使用条款和出版政策可在 https://www.scienceopen.com/ 找到。预印本声明：本文为预印本，尚未经过同行评审，正在考虑并提交给 ScienceOpen Preprints 进行公开同行评审。DOI：10.14293/S2199-1006.1.SOR-.PPVK63O.v2 预印本首次在线发布：2022 年 7 月 25 日 关键词：COVID-19、SVM、神经网络、NLP、数学建模、高斯模型、疫情防控](/simg/8/8dd469c55249d1165cc0c55c494f5b27bda7b11b.png)
文章标题：抗击 COVID-19：人工智能技术与挑战 作者：Nikhil Patel[1]、Sandeep Trivedi[2]、Jyotir Moy Chatterjee[3] 所属机构：毕业于杜比克大学，联系电子邮件 ID：Patelnikhilr88@gmail.com[1]，IEEE 会员，毕业于 Technocrats Institute of Technology，联系电子邮件 ID：sandeep.trived.ieee@gmail.com[2]，尼泊尔加德满都佛陀教育基金会[3] Orcid id：0000-0001-6221-3843[1]、0000-0002-1709-247X[2]、0000-0003-2527-916X[3] 联系电子邮件：sandeep.trived.ieee@gmail.com 许可信息：本作品已以开放获取形式发表根据 Creative Commons 署名许可 http://creativecommons.org/licenses/by/4.0/，允许在任何媒体中不受限制地使用、分发和复制，前提是正确引用原始作品。条件、使用条款和出版政策可在 https://www.scienceopen.com/ 找到。预印本声明：本文为预印本，尚未经过同行评审，正在考虑并提交给 ScienceOpen Preprints 进行公开同行评审。DOI：10.14293/S2199-1006.1.SOR-.PPVK63O.v2 预印本首次在线发布：2022 年 7 月 25 日 关键词：COVID-19、SVM、神经网络、NLP、数学建模、高斯模型、疫情防控
文章标题：抗击 COVID-19：人工智能技术与挑战 作者：Nikhil Patel[1]、Sandeep Trivedi[2]、Jyotir Moy Chatterjee[3] 所属机构：毕业于杜比克大学，联系电子邮件 ID：Patelnikhilr88@gmail.com[1]，IEEE 会员，毕业于 Technocrats Institute of Technology，联系电子邮件 ID：sandeep.trived.ieee@gmail.com[2]，尼泊尔加德满都佛陀教育基金会[3] Orcid id：0000-0001-6221-3843[1]、0000-0002-1709-247X[2]、0000-0003-2527-916X[3] 联系电子邮件：sandeep.trived.ieee@gmail.com 许可信息：本作品已以开放获取形式发表根据 Creative Commons 署名许可 http://creativecommons.org/licenses/by/4.0/，允许在任何媒体中不受限制地使用、分发和复制，前提是正确引用原始作品。条件、使用条款和出版政策可在 https://www.scienceopen.com/ 找到。预印本声明：本文为预印本，尚未经过同行评审，正在考虑并提交给 ScienceOpen Preprints 进行公开同行评审。DOI：10.14293/S2199-1006.1.SOR-.PPVK63O.v2 预印本首次在线发布：2022 年 7 月 25 日 关键词：COVID-19、SVM、神经网络、NLP、数学建模、高斯模型、疫情防控
夏季2024年 - 特警数学/Stat Research
责任：在夏季计划的4周内支持16个夏季学者：作为主题教学助理（TAS），以支持将要教书的教师；每周举行5个学习厅课程；充当RA，提供游览，谈论校园的资源以支持学者，身心健康，社交活动；在计划正式开始之前，接受2周的培训；在夏季参加每周3点员工会议并举行报告；在夏季计划之后的一周内跟进董事
数学-II 课程大纲
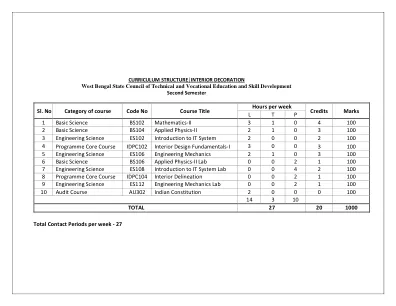
先决条件：掌握基本的坐标几何、统计学和微积分知识 总接触时长：60 小时 目的：数学是工程专业学生的支柱。数学课程根据工程部门的需求不断变化。教学大纲的设计考虑到了各类学生的新兴需求。课程非常重视各种内容的应用。本课程将培养学生进行精确计算的分析能力，并为学生提供继续教育的基础。 课程目标：完成本课程后，学生将能够 i) 应用克莱姆法则和矩阵求逆的知识来寻找线性联立方程的解。ii) 应用直线、圆、圆锥曲线方程解决实际问题。iii) 应用各种积分评估技术和各种寻找一阶和二阶常微分方程的完全原函数的方法来解决工程问题。iv) 使用偏微分的概念来解决物理问题。 v) 分析实际情况下的统计数据和概率。 单元 1 行列式和矩阵 10 小时 1.1 行列式：4 1.1.1 2 阶和 3 阶行列式的定义和展开。子式和余因式 1.1.2 行列式的基本性质（仅限陈述）和简单问题 1.1.3 4 阶行列式的 Chios 方法 1.1.4 用 Cramer 规则解线性联立方程（最多 3 个未知数）。 1.2 矩阵： 1.2.1 矩阵的定义及其阶。 6 1.2.2 不同类型的矩阵。（矩形、方阵、行矩阵、列矩阵、上三角矩阵、下三角矩阵、对角矩阵、标量矩阵、单位矩阵、零矩阵） 1.2.3 两个矩阵相等 1.2.4 矩阵与标量的加法、减法、乘法以及两个矩阵的乘法 1.2.5 矩阵的转置、对称矩阵和斜对称矩阵、简单问题 1.2.6 奇异矩阵和非奇异矩阵、3 阶矩阵的伴随矩阵和逆矩阵
M.Tech。嵌入式和机器学习系统课程和教学大纲-M.Sc.应用数学电子与ICT学院，NIT WARANGAL https://forms.gle/ ...
关于FDP：有关人工智能（AI）的教师发展计划（FDP），用于计算机视觉，医学成像应用将帮助教育者和研究人员了解AI基础知识及其如何应用于具有多个安全应用的医学成像技术。参与者将探索机器学习和深度学习概念，专注于使用AI进行医学成像，这有助于诊断，医疗保健，农业，零售和监视系统。AI通过基于面部识别，虹膜识别，指纹分析和语音识别的准确有效的身份验证方法，在计算机视觉中起关键作用。通过实践活动和实例实例，与会者将获得实用技能，可以在教学和研究中有效地使用不同的AI使用AI。在计划结束时，参与者将准备将AI工具集成到他们的工作中，提高他们通过现代技术教授和解决安全挑战的能力。这将通过增强他们在这些关键领域的专业知识和教学能力来使参与者受益。主要课程内容：针对计算机视觉应用程序的最新实施介绍。机器学习基础知识，使用数据预处理和数据可视化。监督和无监督的学习方法，SVM分类，神经网络和应用程序。深度学习方法的简介和基于DL的其他架构及其应用程序。用于计算机视觉，生物特征和医学成像实现的深度学习体系结构。使用Python/Matlab的动手会话。医学图像数据处理和分析。用于生物医学成像，基于CT扫描/MRI的图像分析，眼底和医学图像分类的AI/ML。对象检测/跟踪算法（例如Yolo等），诸如UNET等分段算法等使用张量流/Pytorch识别人类活动/动作/生物识别识别张量流/keras/pytorch/jupyter和colab的基础知识。使用Python/Matlab使用数据预处理和数据可视化。CV和AI算法在硬件平台上实现，例如Jetson Nano，TX2和Pynq等。主持此计划的教师：该计划将由Nit Warangal的教职员工进行；邀请来自IIT/NIT/IIIT的有关领域的院士在该计划中发表讲座。也有望作为课程的一部分提供行业的演讲者。
数学 | AI 快照 | aiEDU
为什么是人工智能？在未来几十年，人工智能将影响学生从事的任何职业领域、他们使用的任何消费产品以及影响他们生活的政策。事实上，你可以打赌你的学生已经在日常生活中与人工智能互动了。每天接触人工智能将使你的学生获得成功所需的知识。
应用数学重点 2022-23
额外学位要求：要获得南犹他大学学士学位，学生必须总共修满 40 个高年级学分。应用数学专业的学生可能需要在其专业要求之外修满最多 14 个额外的高年级选修课。他们可能还需要多达 35 个选修学分才能满足 120 个学分的学位要求。数学系强烈建议那些寻求应用数学学位的学生修读化学、计算机科学或物理学的辅修课程。每个辅修课程的信息都包含在下页的表格中。
对数学专家和新手的高密度脑电图数据的非线性和机器学习分析
神经科学的当前趋势是使用自然主义刺激，例如电影，课堂生物学或视频游戏，旨在在生态上有效的条件下了解大脑功能。自然主义刺激招募复杂和重叠的认知，情感和感觉脑过程。大脑振荡形成了此类过程的基本机制，此外，这些过程可以通过专业知识来修改。尽管大脑作为生物系统是高度非线性的，但通常通过线性方法分析人类皮质功能。这项研究应用了一种相对健壮的非线性方法，即Higuchi分形维度（HFD），将数学专家和新手的皮质功能分类为在脑电图实验室中解决长期且复杂的数学示范。脑成像数据是在自然主义刺激期间长期跨度收集的，可以应用数据驱动的分析。因此，我们还通过机器学习算法探讨了数学专业知识的神经标志。需要新颖的方法来分析自然主义数据，因为基于还原主义和简化研究设计的现实世界中脑功能的理论的表述既具有挑战性又可疑。数据驱动的智能方法可能有助于开发和测试有关复杂大脑功能的新理论。我们的结果阐明了HFD在复杂数学期间对数学专家和新手分析的不同神经签名，并将机器学习作为一种有前途的数据驱动方法，以了解专业知识和数学认知的大脑过程。
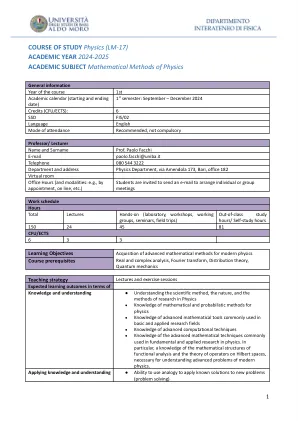
物理学的数学方法
o 获得持续学习和知识更新的基本知识工具 o 学生将培养不断更新物理研究中的数学技术和技能的态度。 教学大纲 内容知识 度量空间。定义。例子。开集、闭集、邻域。拓扑空间。连续映射。稠密集、可分空间。收敛和柯西序列。完备性。例子。度量空间的完备性。巴拿赫空间。向量空间。范数空间。完备性和巴拿赫空间。例子：有限维空间、序列空间、函数空间。有界线性算子。连续性和有界性。BLT 定理。连续线性泛函和对偶空间。有界线性算子的巴拿赫空间。例子。测度论简介。勒贝格积分。Sigma 代数和 Borel 测度。可测函数。支配和单调收敛。富比尼定理。例子：绝对连续测度、狄拉克测度、康托测度。勒贝格分解定理。希尔伯特空间。内积。欧几里得空间和希尔伯特空间。正交性、勾股定理。贝塞尔不等式和柯西-施瓦茨不等式。三角不等式。平行四边形定律和极化恒等式。例子。直和。投影定理。Riesz-Fréchet 引理。正交系统和傅里叶系数。正交基和 Parseval 关系。Gram-Schmidt 正交化程序。与 l^2 同构。张量积和积基。希尔伯特空间上的线性算子。有界算子的 C ∗ -代数。正规、自伴、酉和投影算子。Baire 范畴定理。一致有界性原理。一致、强和弱收敛。一些量子力学。无界算子。伴生。对称和自伴算子。例子：乘法和导数算子。本质自伴算子。自伴性和本质自伴性的基本标准。图、闭包
数字理论硕士数学
1 Arrithmetic Welfares 1 1.1 Arrithmetic函数。。。。。。。。。。。。。。。。。。。。。。。。1.1.1。。。。。。。。。。。。。。。。。1.1.2可维护函数ϕ（n）。。。。。。。。。。。。。。。。。3 1.1.3关系。。。。。。。。。。。。。。。4 1.1.4 ϕ（n）的产品。。。。。。。。。。。。。。。。5 1.1.5弧形功能。。。。。。。。。9 1.1.6 Dirichlet倒置和Mobius倒置公式。。。。。12 1.1.7 Mangoldt函数λ（n）。。。。。。。。。。。。。。。。15 1.1.8乘法函数。。。。。。。。。。。。。。。。。。。16 1.1.9完全乘法功能的示例。。。。。。20 1.1.10乘法函数的示例。。。。。。。。。。。。20 1.1.11乘法函数和DIRICHLET乘法。。。21 1.1.12完全乘法函数的倒数。。。。24 1.1.13 liouville的功能λ（n）。。。。。。。。。。。。。。。。。。。28 1.1.14除数函数σα（n）。。。。。。。。。。。。。。。。。30 1.1.15广义卷积。。。。。。。。。。。。。。。。。。。32 1.1.16算术函数的衍生物。。。。。。。。。。。。34 1.1.17 Selberg身份。。。。。。。。。。。。。。。。。。。。。36 1.1.18练习。。。。。。。。。。。。。。。。。。。。。。。。。。。37 1.2算术函数的平均值。。。。。。。。。。。。。。。。。38 1.2.1大oh符号。具有函数的准确性。。39 1.2.2 Dirichlet的政党。。。。。。。。。。。。。46 1.2.3。。。。。。。。。。。。。。48 1.2.4。。。。。。。。。。。。。。。。。。。。。。。。。。55