XiaoMi-AI文件搜索系统
World File Search System数学
环境管理的数学建模
环境与生物物种相关，无论大小如何。不管知道环境变化会对所有物种的生活方式产生不利影响，人类都会通过从人工来源中散发出有害的气体来污染环境。人类正在迅速发明并发现出于各种目的的新技术。但是，大多数技术会散发有害和有毒的温室气体（GHG），这些气体（GHG）限制了地球温度并引起全球变暖。因此，由于温室气体的快速排放和环境中的浓度，全球变暖持续了，其影响会改变气候系统并损害沿海和海洋生态系统。此外，快速的全球变暖和温室气体排放量通过工业区域周围的酸雨引起海水和森林生态系统的酸化，损害了海洋生态系统。结果，沿海和海洋生态系统中对温度敏感的物种通常日常消失。另一方面，尽管知道森林地区的重要性，但我们不加选择地砍伐树木并破坏了森林地区的各种目的。因此，环境中纯氧的缺乏正在显着增加，我们周围的大气变得更加温暖和污染。根据环境科学家的说法，如果情况继续进行，则数千种对温度敏感的物种可能灭绝，导致到当前世纪末的生态失衡。本书由十个章节组成，如下所示：本书的主要目的是通过减轻潜在的影响来研究沿海和海洋生态系统的快速全球变暖和温室气体排放对沿海和海洋生态系统的潜在影响。
数学常数的统一共振模型
数学常数（例如π，E和φ）长期以来一直被认为是天然系统中几何，生长和自组织的基础。然而，常规数学将这些数字视为独立领域的新兴特性（几何，微积分和数字理论），而不是统一框架内的内在共振状态。动态新兴系统（代码）的手性提出，这些常数不是任意的，而是在主要驱动的共振字段中作为必要的相锁定结构出现。
![文章标题：抗击 COVID-19：人工智能技术与挑战 作者：Nikhil Patel[1]、Sandeep Trivedi[2]、Jyotir Moy Chatterjee[3] 所属机构：毕业于杜比克大学，联系电子邮件 ID：Patelnikhilr88@gmail.com[1]，IEEE 会员，毕业于 Technocrats Institute of Technology，联系电子邮件 ID：sandeep.trived.ieee@gmail.com[2]，尼泊尔加德满都佛陀教育基金会[3] Orcid id：0000-0001-6221-3843[1]、0000-0002-1709-247X[2]、0000-0003-2527-916X[3] 联系电子邮件：sandeep.trived.ieee@gmail.com 许可信息：本作品已以开放获取形式发表根据 Creative Commons 署名许可 http://creativecommons.org/licenses/by/4.0/，允许在任何媒体中不受限制地使用、分发和复制，前提是正确引用原始作品。条件、使用条款和出版政策可在 https://www.scienceopen.com/ 找到。预印本声明：本文为预印本，尚未经过同行评审，正在考虑并提交给 ScienceOpen Preprints 进行公开同行评审。DOI：10.14293/S2199-1006.1.SOR-.PPVK63O.v2 预印本首次在线发布：2022 年 7 月 25 日 关键词：COVID-19、SVM、神经网络、NLP、数学建模、高斯模型、疫情防控](/simg/8/8dd469c55249d1165cc0c55c494f5b27bda7b11b.png)
文章标题：抗击 COVID-19：人工智能技术与挑战 作者：Nikhil Patel[1]、Sandeep Trivedi[2]、Jyotir Moy Chatterjee[3] 所属机构：毕业于杜比克大学，联系电子邮件 ID：Patelnikhilr88@gmail.com[1]，IEEE 会员，毕业于 Technocrats Institute of Technology，联系电子邮件 ID：sandeep.trived.ieee@gmail.com[2]，尼泊尔加德满都佛陀教育基金会[3] Orcid id：0000-0001-6221-3843[1]、0000-0002-1709-247X[2]、0000-0003-2527-916X[3] 联系电子邮件：sandeep.trived.ieee@gmail.com 许可信息：本作品已以开放获取形式发表根据 Creative Commons 署名许可 http://creativecommons.org/licenses/by/4.0/，允许在任何媒体中不受限制地使用、分发和复制，前提是正确引用原始作品。条件、使用条款和出版政策可在 https://www.scienceopen.com/ 找到。预印本声明：本文为预印本，尚未经过同行评审，正在考虑并提交给 ScienceOpen Preprints 进行公开同行评审。DOI：10.14293/S2199-1006.1.SOR-.PPVK63O.v2 预印本首次在线发布：2022 年 7 月 25 日 关键词：COVID-19、SVM、神经网络、NLP、数学建模、高斯模型、疫情防控
文章标题：抗击 COVID-19：人工智能技术与挑战 作者：Nikhil Patel[1]、Sandeep Trivedi[2]、Jyotir Moy Chatterjee[3] 所属机构：毕业于杜比克大学，联系电子邮件 ID：Patelnikhilr88@gmail.com[1]，IEEE 会员，毕业于 Technocrats Institute of Technology，联系电子邮件 ID：sandeep.trived.ieee@gmail.com[2]，尼泊尔加德满都佛陀教育基金会[3] Orcid id：0000-0001-6221-3843[1]、0000-0002-1709-247X[2]、0000-0003-2527-916X[3] 联系电子邮件：sandeep.trived.ieee@gmail.com 许可信息：本作品已以开放获取形式发表根据 Creative Commons 署名许可 http://creativecommons.org/licenses/by/4.0/，允许在任何媒体中不受限制地使用、分发和复制，前提是正确引用原始作品。条件、使用条款和出版政策可在 https://www.scienceopen.com/ 找到。预印本声明：本文为预印本，尚未经过同行评审，正在考虑并提交给 ScienceOpen Preprints 进行公开同行评审。DOI：10.14293/S2199-1006.1.SOR-.PPVK63O.v2 预印本首次在线发布：2022 年 7 月 25 日 关键词：COVID-19、SVM、神经网络、NLP、数学建模、高斯模型、疫情防控
CSJM大学，Kanpur NEP计划2024-25 BA-I学期 国际会议 e0025关于NEP奇数学期计划2024-25.pdf vko'; d lwpuk 校园考试时间表（奇数SEM）2024-25 医疗保健新时代的药物创新 b'' 入学手册2024-25 最终SBS chhatrapati shahu ji ji maharaj大学，坎普尔 NEP甚至学期考试方案。 2023-24 dk; kzy; kki
现代世界的历史（公元1453年 - 1815a.d。）/中世纪印度的社会和经济历史（1200a.d.-公元1700年） /历史上的道德规范28-01-2025哲学哲学哲学哲学（印度和西方）梵语A020501T vaidik vaidik vaikya vakya evam evam evam evam evam evam evam evam bhartiya darsried哲学 A020502T Vykaran Evam Bhasha Vigyan 30-01-2025 02:30 PM To 04:30 PM Thursday BA-V Drawing & Painting A140501T History of Indian Architecture 31-01-2025 02:30 PM To 04:30 PM Friday BA-V Drawing & Painting A140502T History of Indian Art - 2 01-02-2025 02:30 PM To 04:30下午星期六BA-V音乐声音A320501T西方音乐科学，印度音乐风格，03-02-2025 02:30 pm至04:30 pm星期一BA-V音乐声音A320503T应用Ragas和Taals Applied理论04-02-2025 02-2025 02:30 pm至04:30 PM星期二BA-v Mustice pla-v Music taper plapan ba-v Music plapla a310503 05-02-2025 02:30 pm至04:30 pm星期三星期三BA-V体育E020501T运动受伤和物理疗效06-02-2025 02:30 02:30 pm至04:30 pm至04:30 ba-V体育运动E020502T运动学和体育运动学
数学中的认知进入特征-Earnia
学生的特征。但是，似乎没有研究将这些特征与学生在定量化学方面的成就相关。因此，这项研究研究了数学和教学效率的认知进入特征与学生在定量化学方面的成就相关的程度。该研究采用了描述性研究设计。简单的随机抽样用于在河流州选择3个地方政府区域（LGA），每所LGA的10所学校以及一个由每所学校的所有化学学生组成的科学课程。共有1652名学生参加了这项研究。数据收集工具包括：数学测试中的CEC，学生的TE等级和定量化学成就测试。使用多重回归分析数据。CEC在数学和TE中对学生在
数学经济学在解释经济体经济增长中，内源性和外源技术变革
经济增长是经济经济政策中不同生产力因素之间相互作用的函数，尤其是它可以用劳动力，生产资源（土地，资本）和技术等方面表达。 div>这项工作旨在采用一个模型来解释发展中经济体的经济增长，该模型是根据上述因素提出了这种增长的模型。然后根据资本和工作提出生产，并调整了两个模型，一种具有外在技术变化，另一种暗示了内源性的技术变化。 div>该模型是通过具有恒定替代弹性的生产函数开发的，因此它适用于发达和发展经济体，因为预计在经济体中会发展出替代经济增长的弹性。 div>研究使我们能够开发
数字化游戏化学习与数学游戏应用对四年级学生计算能力的影响 刘濝濢 -Bei LIU a* , Alex W
运用数学游戏应用进行数字化游戏化学习对四年级学生计算能力的影响 刘濝濢 -Bei LIU a* , Alex Wing Cheung TSE b* 香港大学教育学院，香港 a* u3598295@connect.hku.hk; b* awctse@hku.hk 摘要：计算能力是小学数学学习中必不可少的素质，事实证明，通过游戏化应用进行学习可以提高学生的数学学习成绩，从而有利于发展他们的计算能力。计算能力是数学核心技能之一，可以通过不断的计算练习来提高。然而，目前关于在小学使用运用数学游戏应用进行数字化游戏化学习 (DGBL) 对发展学生计算能力的影响的研究还很少。因此，本项准实验研究共有78名学生参与，旨在评估通过iPad进行DGBL与数学游戏应用“口算英雄”对中国大陆一所主流学校四年级学生计算能力的可能影响。实验班将数学游戏应用融入为期四周的课堂活动中，实验组和对照组均采用标准化计算能力测试：Abilita diCalcoloz计算能力-记忆与训练第6-11组（Cornoldi等，2002）进行前测和后测。采用方差分析的数据分析结果显示，在数学课堂上使用iPad上的数学游戏应用学习时，学生的计算能力存在显著差异，四年级实验组（n=40）与对照组（n=38）的整体计算能力存在显著差异。换句话说，我们发现，在使用数学游戏应用进行计算练习后，学生更有可能获得更好的计算能力，尤其体现在计算速度更快、错误率更低方面。然而，在数值知识方面没有显著差异，使用这种数学游戏应用程序学习可能不会导致获得更多的数学知识。这项研究为小学数学教育者和教师提供了一个现实的视角来了解使用数学游戏应用程序学习的潜力：它可以成为提高四年级学生计算能力的有效工具。该项目的第二阶段是探索研究结果背后的原因，揭示使用数学游戏应用程序进行 DGBL 的可能因素，这些因素可能会促进计算能力的某些方面。提出了将 DGBL 融入小学数学课堂的进一步建议。关键词：基于数字游戏的学习、计算能力、数学游戏 1。引言：学生的计算能力是指理解数字之间规律和相对量，并以更灵活的方式进行数字运算（加、减、乘、除）的能力（Feigenson 等，2004；Tall 和 Dehaene，1998）。计算能力对于小学阶段的数学成绩至关重要（Cowan 等，2011）。与不同领先国家的小学数学课程类似，根据中国大陆最新的课程标准，四年级学生必须掌握四种运算（加、减、乘、除），并且需要不断练习计算能力以找到更简单的解决方案（中华人民共和国教育部，2022）。学生的表现和
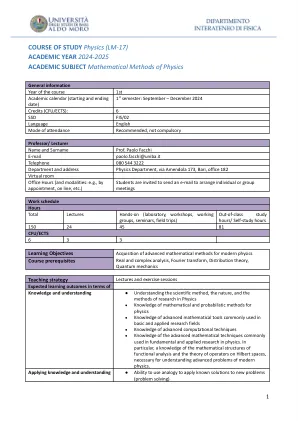
物理学的数学方法
o 获得持续学习和知识更新的基本知识工具 o 学生将培养不断更新物理研究中的数学技术和技能的态度。 教学大纲 内容知识 度量空间。定义。例子。开集、闭集、邻域。拓扑空间。连续映射。稠密集、可分空间。收敛和柯西序列。完备性。例子。度量空间的完备性。巴拿赫空间。向量空间。范数空间。完备性和巴拿赫空间。例子：有限维空间、序列空间、函数空间。有界线性算子。连续性和有界性。BLT 定理。连续线性泛函和对偶空间。有界线性算子的巴拿赫空间。例子。测度论简介。勒贝格积分。Sigma 代数和 Borel 测度。可测函数。支配和单调收敛。富比尼定理。例子：绝对连续测度、狄拉克测度、康托测度。勒贝格分解定理。希尔伯特空间。内积。欧几里得空间和希尔伯特空间。正交性、勾股定理。贝塞尔不等式和柯西-施瓦茨不等式。三角不等式。平行四边形定律和极化恒等式。例子。直和。投影定理。Riesz-Fréchet 引理。正交系统和傅里叶系数。正交基和 Parseval 关系。Gram-Schmidt 正交化程序。与 l^2 同构。张量积和积基。希尔伯特空间上的线性算子。有界算子的 C ∗ -代数。正规、自伴、酉和投影算子。Baire 范畴定理。一致有界性原理。一致、强和弱收敛。一些量子力学。无界算子。伴生。对称和自伴算子。例子：乘法和导数算子。本质自伴算子。自伴性和本质自伴性的基本标准。图、闭包
K-12 数学采用公共访问.pdf
nglsync.cengage.com student01@ocpsmath2021discrete.comWelcome1 可以从试用版 NGLSync 门户访问这些帐户。学校名称应为“试用版学校”，密码为 Welcome1。一次只能有一个人使用模拟帐户查看。单击“启动课程”进入 WebAssign。选择我的电子书或滚动到页面底部并单击书籍封面进行查看。金融代数 Savvas Learning Company LLC 定量思维：用数字沟通 2e c2020 (Gaze) [FL Math for Data & Fin Lit - Regular]