XiaoMi-AI文件搜索系统
World File Search System普通微分方程中的第二个课程
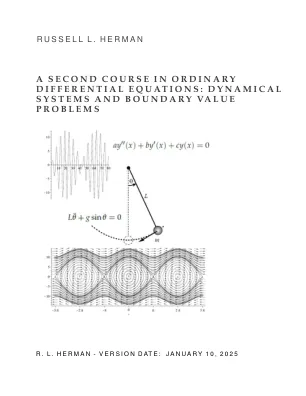
1简介1 1。1对第一门课程的评论。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 2 1。 1。 1一阶微分方程。 。 。 。 。 。 。 。 。 。 。 。 2 1。 1。 2秒阶线性微分方程。 。 。 。 。 。 6 1。 1。 3恒定系数方程。 。 。 。 。 。 。 。 。 。 。 。 。 。 7 1。 1。 4未确定系数的方法。 。 。 。 。 。 。 。 。 。 9 1。 1。 5 Cauchy-Euler方程。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 13 1。 2课程概述。 。 。 。 。 。 。 。1对第一门课程的评论。。。。。。。。。。。。。。。。。。。。。2 1。1。1一阶微分方程。。。。。。。。。。。。2 1。1。2秒阶线性微分方程。。。。。。6 1。1。3恒定系数方程。。。。。。。。。。。。。。7 1。1。4未确定系数的方法。。。。。。。。。。9 1。1。5 Cauchy-Euler方程。。。。。。。。。。。。。。。。。。13 1。2课程概述。。。。。。。。。。。。。。。。。。。。。。15 1。3附录:减少顺序和复杂根。。。。。。16 1。4个应用程序。。。。。。。。。。。。。。。。。。。。。。。。。。。。。18 1。4。1个质量弹簧系统。。。。。。。。。。。。。。。。。。。。19 1。4。2简单的摆。。。。。。。。。。。。。。。。。。。20 1。4。3 LRC电路。。。。。。。。。。。。。。。。。。。。。。。。20 1。4。4曲线的正交轨迹*。。。。。。。。。。。。21 1。4。5追踪曲线*。。。。。。。。。。。。。。。。。。。。。。。22 1。5其他一阶方程*。。。。。。。。。。。。。。。。。。。27 1。5。1 Bernoulli方程*。。。。。。。。。。。。。。。。。。。。27 1。5。2 Lagrange和Clairaut方程*。。。。。。。。。。。。28 1。5。。3 riccati方程*。。。。。。。。。。。。。。。。。。。。。31个问题。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。32
计算数学BS(计算...
CM-301 Calculus ( 3 + 0 ) Limits & Continuity: Limits, Continuity, Tangent lines & Rate of Change, Sequence and Series: Sequence and Their Divergence and Convergence Test, Introduction to Infinite Series, Taylor and Maclaurin Series, Convergence and Divergence Test for Series: Limit comparison test, Ratio test, Root test, Derivatives: Techniques of differentiation, Chain rule and implicit differentiation, derivatives逆函数,双曲线函数,逆三角和双曲线函数,分化的应用,最大值和最小值单个可变功能的功能,边际分析,边际分析以及使用不确定的形式和l'医院规则,整体构成:riemann积分,整合和整合的序列,差异和整合的序列,依次和整合三角学和双曲线功能,正弦,余弦,割线和切线的功能的整合,部分,三角替代,不当积分,beta和伽玛积分,差异方程,差分方程:微分方程,形成和解决方程,方程,方程,一阶,初始和边界价值,求解一级方程式或求解的各种方程式,确切的既方程式,既有方程式,又有等方程,并依次分离,既有等方程,又有等方程,并依次分离,且既有等方程,又依次,既有等方程式,又依次分离,及以上等方程式,且共同依次,既有方程性,又有方程性的范围。轨迹。非线性一阶方程,信封和单数解决方案
经典电动力学中的排斥相互作用
摘要:在此,我们在感应方程(麦克斯韦方程之一)中引入了一个附加项。应用标量和矢量势的相关拉格朗日形式适用于此修改的麦克斯韦方程。在哈密顿原理的框架内,我们能够推导出场变量电场 E 和磁感应 B 具有负“质量项”的克莱因-戈登方程。我们可以从方程的数学结构得出结论,出现了排斥相互作用。可以计算出当前情况下的惠勒传播子,由此可以讨论场的时间演化。尽管这些方程具有快子解,但结果符合因果关系原理。根据该理论,场中可能会出现自发电荷分离过程。
PPH312高级量子力学
相对论量子力学:klein-gordon方程,狄拉克方程及其平面波解,具有库仑电势的粒子的klein gordan方程的溶液,负能量溶液的重要性,dirac粒子的旋转角动量。dirac方程的非相关限制,中央场中粒子的dirac方程,氢原子的精细结构,羔羊移位。
过渡湍流和充分发展湍流中的随机性
我们已经写出了水流方程。从实验中,我们找到了一组概念和近似值来讨论解决方案——涡街、湍流尾流、边界层。当我们在不太熟悉的情况下遇到类似的方程,并且还不能进行实验时,我们会尝试以一种原始、停滞和混乱的方式求解方程,以确定可能出现哪些新的定性特征,或者哪些新的定性形式是方程的结果。
量子电路完整性:扩展和简化
尽管量子电路在量子计算中已经无处不在,但量子电路的第一个完整方程理论直到最近才引入。完整性保证量子电路上的任何真实方程都可以从方程理论中得出。我们通过两种方式改善了这种完整性结果:(i)我们通过证明可以从其余规则得出几个规则来简化方程理论。特别是,在三个最复杂的规则中,有两个被删除,第三个规则略微简化。(ii)可以将完整的方程理论扩展到带有Ancillae或Qubit的量子电路,以使用其他工作空间和混合量子计算分别表示量子计算。我们表明,在这些更具表现力的设置中可以极大地简化剩余的复杂规则,从而导致方程理论所有方程式在有限数量的Qubits上作用。为表达量子电路模型的简单和完整的方程理论的发展开辟了有关量子电路推理的新途径。它为各种编译任务提供了强大的正式基础,例如电路优化,硬件约束满意度和验证。
STAAR 标准快照 – 代数 I
A.6(B) 给定顶点和图上的另一点,写出二次函数方程,以顶点形式写出方程( f ( x ) = a ( x – h ) 2 + k ),并将方程从顶点形式重写为标准形式( f ( x ) = ax 2 + bx + c )
不均匀的布里鲁因区取样对于晶体固体中激子结合能的伯特 - 盐盐方程
1 KBR,Inc,NASA AMES研究中心,加利福尼亚州莫菲特菲尔德,美国2材料科学部,劳伦斯·伯克利国家实验室,加利福尼亚州伯克利,加利福尼亚州94720,美国3美国3号物理学系美国伯克利,94720,美国5材料科学与工程系,斯坦福大学,斯坦福大学,加利福尼亚州斯坦福大学94305,美国6斯坦福大学材料与能源科学研究所,SLAC国家加速器实验室,加利福尼亚州Menlo Park,加利福尼亚州Menlo Park,94025,美国7机械工程和材料科学系,纽约大学,纽约大学,纽约市765111111111。 OX1 3PJ,英国9 Kavli Energy Nanoscience Institute,位于伯克利,伯克利94720,美国