XiaoMi-AI文件搜索系统
World File Search System随机变量的期望值与标准差
我们感兴趣的问题不仅是关于随机变量的分布或其概率,而且我们可能想要确定随机变量的“平均值”或期望值,以及它与其期望值或标准差的偏差程度。我们将只研究离散随机变量的期望值和标准差,这些离散随机变量是其可能值集合形成可数不同值列表的随机变量。例如,博兹曼医院接下来的三胎女孩数量就是一个离散随机变量,因为它只能取值 0、1、2 或 3。离散随机变量可以取无限数量的可能值,只要我们能够将它们列在有序列表中。例如,掷硬币直到第一次出现正面的次数是一个离散随机变量,可能值为 1、2、3、4、...可以在某个间隔内取任意值的随机变量(例如时间、长度、利率、高度)称为连续随机变量。我们将使用以下符号来指定离散随机变量可能结果的概率:
文章 基于量子期望值的语言模型及其在问答中的应用
摘要:量子语言模型由于其透明性和可解释性而被引入信息检索。尽管取得了令人振奋的进展,但当前的研究主要研究语义希尔伯特空间的差异句子子空间的密度矩阵之间的关系。整个希尔伯特空间具有唯一的密度矩阵,但还缺乏探索。在本文中,我们提出了一种基于量子期望值的语言模型(QEV-LM)。为语义希尔伯特空间构建了一个唯一的共享密度矩阵。在这个量子模型中,单词和句子被视为不同的可观测量。在此背景下,描述问答对之间相似度的匹配分数自然地被解释为联合问答可观测量的量子期望值。除了理论合理性之外,在 TREC-QA 和 WIKIQA 数据集上的实验结果证明了我们提出的模型具有出色的计算效率和较低的时间消耗。
补充信息:估计多个期望值的近似最优量子算法
本信重点关注估计纯态 | ψ ⟩ 的多个可观测量的期望值的任务。在状态准备成本为主导因素的环境中,我们主要量化 Oracle 模型中所需的资源,在该模型中我们计算对状态准备幺正及其逆的调用次数。为了为该成本模型和一般任务提供具体的动机,考虑以下示例,其中我们感兴趣的状态是 Jordan-Wigner 变换下某些二阶量子化电子结构哈密顿量的未知基态。在这种情况下,状态准备步骤预计在某些假设下是可处理的,但相对昂贵,即使使用现代方法(例如,通过应用参考文献 1、2 的基态准备算法结合最先进的哈密顿量块编码技术 [ 3、4 ])。同时,感兴趣的可观测量可能特别简单(例如,费米子约化密度矩阵的元素)。在补充信息第 VI 部分中,我们讨论了状态准备成本不一定占主导地位的情况,以及在我们的方法背景下可能存在的权衡。令 U ψ 表示从 | 0 ⟩ 状态准备 | ψ ⟩ 的幺正态,令 { O j } 为 M 个 Hermitian 算子的集合。为了简化与现有方法的比较,我们在本节中做出额外假设,即 O j 也是幺正态,尽管可以使用基于块编码的技术放宽这一要求 [ 5 ]。与正文一样,我们的目标是尽量减少对 U ψ 和 U † ψ 的调用次数,以获得 M 个期望值 ⟨ ψ | O j | ψ ⟩ 的估计 eoj,使得
投资组合保险策略
同样,由于没有套利,对于风险资产的所有终值,两种收益都不会大于另一种。如附录 3 所示,ν T 的期望值高于 Black 和 Scholes 模型。它特别解释了为什么对于 CPPI,BS 模型的期望值高于 SV 模型(见表 1)。B. 期望值、方差、偏度和峰度的比较。处理期权时,均值-方差方法并不总是合理的,因为收益不是线性的。因此,我们同时检查前四个矩。如果我们比较前两个矩(均值-方差分析),请注意,对于 m 高,CPPI 投资组合的期望值和方差大于 OBPI 投资组合的期望值和方差,因此在均值-方差标准方面不存在优势。对于金融市场的任何参数化,至少存在一个 m 值,使得 OBPI 策略在均值-方差意义上优于 CPPI 策略。
基于最大熵形式的量子态层析成像变分方法
图 3:对于范围从 2 到 6 的量子比特,该图显示了在每一步优化中使用重建的量子态获得的 Hermitian 算子的 IC 集的真实期望值和生成的期望值之间的时期数的函数即均方误差 (MSE) 损失。
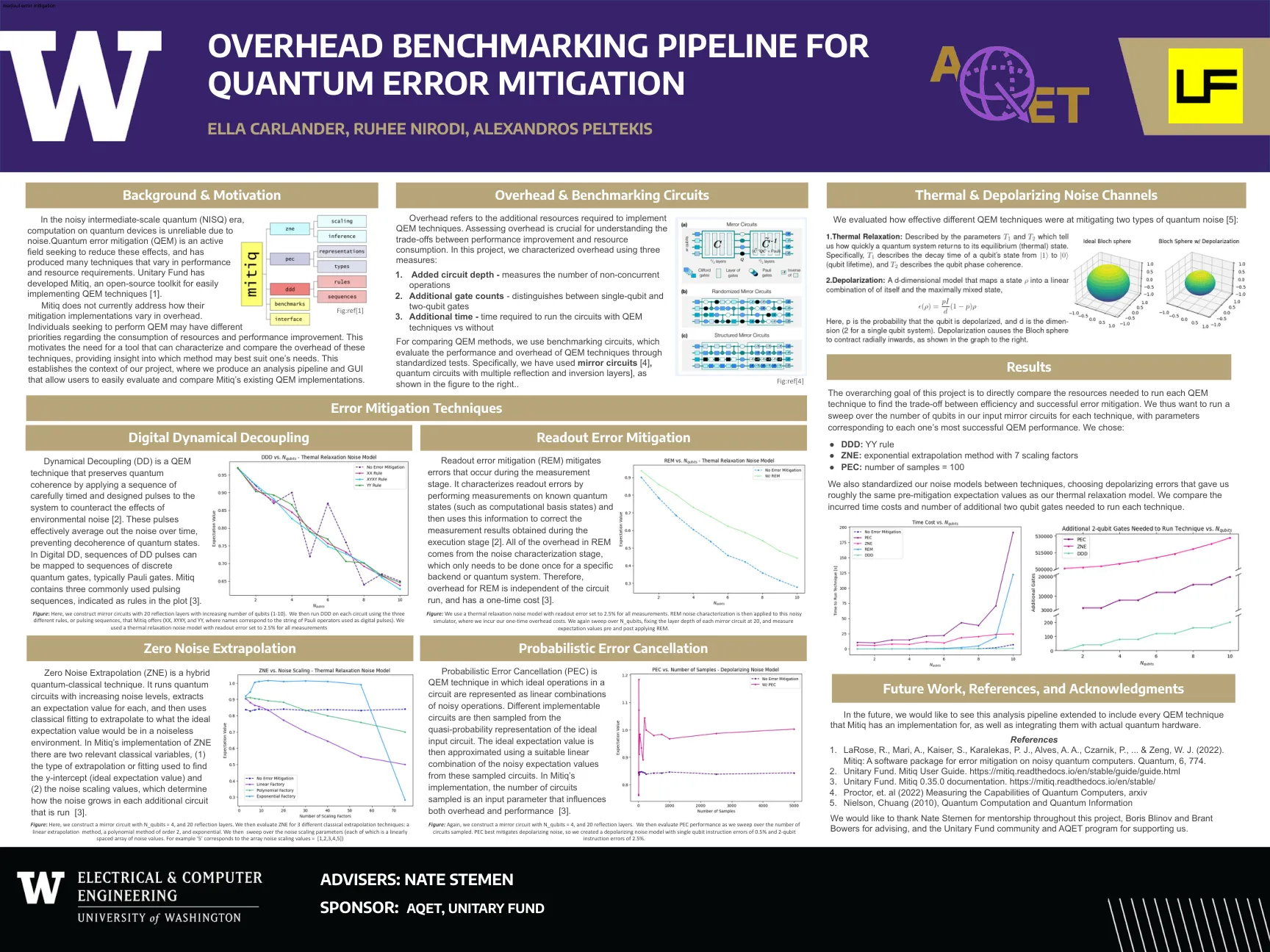
用于缓解量子误差的开销基准测试管道
零噪声外推 (ZNE) 是一种量子经典混合技术。它运行噪声水平不断增加的量子电路,提取每个电路的期望值,然后使用经典拟合外推无噪声环境中的理想期望值。在 Mitiq 的 ZNE 实现中,有两个相关的经典变量:(1) 用于查找 y 截距(理想期望值)的外推或拟合类型和 (2) 噪声缩放值,它们决定了噪声在运行的每个附加电路中如何增长 [3]。
第 7 章 半经典极限——GR 和 LQG
对于像哈密顿约束这样的图变换算子,定义相干(或半经典)状态变得极其困难。也就是说,用经典相空间中的点标记的状态,算子假设一个期望值,该期望值重现了相空间中该点处相应经典函数的值,并且相对于该期望值的(相对)波动很小。发生这种情况的原因是,LQG [] 的现有相干态是在一组有限的有限图上定义的,这些图非常有效地抑制了给定图标记的自由度的波动。然而,哈密顿约束为它们作用的状态增加了自由度,因此这些自由度的波动不再受到抑制。事实上,哈密顿约束相对于这些相干态的半经典行为相当糟糕。
非共同信息几何
1量子概率1 1.1简介。。。。。。。。。。。。。。。。。。。。。。。。。。。。。1 1.2量子期望。。。。。。。。。。。。。。。。。。。。。。。。2 1.2.1 N-N矩阵的代数。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 2 1.2.2期望值。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 3 1.2.3密度矩阵。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。2 1.2.1 N-N矩阵的代数。。。。。。。。。。。。。。。2 1.2.2期望值。。。。。。。。。。。。。。。。。。。。。3 1.2.3密度矩阵。。。。。。。。。。。。。。。。。。。。。。4 1.2.4经典概率。。。。。。。。。。。。。。。。。。。。5 1.2.5笔记。。。。。。。。。。。。。。。。。。。。。。。。。。。。5 1.3条件概率。。。。。。。。。。。。。。。。。。。。。。6 1.3.1经验数据。。。。。。。。。。。。。。。。。。。。。。。6 1.3.2更新。。。。。。。。。。。。。。。。。。。。。。。。。。7 1.3.3破坏统计独立性。。。。。。。。。。。。7 1.4历史实验。。。。。。。。。。。。。。。。。。。。。。。8 1.4.1 EPR悖论。。。。。。。。。。。。。。。。。。。。。。8 1.4.2钟的不平等。。。。。。。。。。。。。。。。。。。。10
“量子力学,理论最小值”的练习
𝜏 𝑧 |𝑢⟩= |𝑢⟩ 和 𝜏 𝑧 |𝑑⟩= −|𝑑⟩ 𝜏 𝑥 |𝑢⟩= |𝑑⟩ 和 𝜏 𝑥 |𝑑⟩= |𝑢⟩ 𝜏 𝑦 |𝑢⟩= 𝑖|𝑑⟩ 和 𝜏 𝑦 |𝑢⟩= −𝑖|𝑢⟩ 写出张量积状态的所有可能组合的方程 𝜎 𝑧 |𝑢𝑢⟩= |𝑢𝑢⟩ 等。练习 6.5 证明以下定理:当以下任何一个Alice 和 Bob 的自旋算子作用于乘积状态,结果仍然是乘积状态。证明在乘积状态下,𝜎̅ 或 𝜏̅ 的任何分量的期望值与在单个单自旋状态下的期望值相同。练习 6.6 假设 Charlie 已准备好单重态中的两个自旋。这一次,Bob 测量 𝜏 𝑦 ,Alice 测量 𝜎 𝑥 。𝜎 𝑥 𝜏 𝑦 的期望值是多少?这说明两次测量之间的相关性如何?