XiaoMi-AI文件搜索系统
World File Search System概率论
CHAP E4120 Ben O'Shaughnessy 教授 3 分 先决条件：热力学、初等概率论和统计过程、微积分。
课程背景 统计力学解释热力学并能够根据分子计算材料特性。 当热力学刚刚发展起来时，人们并不知道物质是由分子组成的！因此，热力学定律的起源也是未知的。 (1) 热力学并没有告诉我们定义材料的状态函数是什么，E(S,V,N) 还是 F(T,V,N) 还是 G(T,P,N) 还是 H(S,P,N) 等。这些函数是热力学定律的输入数据，必须针对每种材料进行测量。我们不能使用热力学来计算这些函数。 (2) 热力学也没有基本的微观基础——它基于经验假设。第二定律和熵特性的存在基于经验假设，通常是“热量不会自发地从一个物体流向另一个更热的物体。”为什么这是真的？热力学无法回答这个问题。统计力学给出了答案，而且非常简单。1874 年，奥地利物理学家路德维希·玻尔兹曼 (Ludwig Boltzmann) 提出了著名的熵假说，将宏观（热力学）世界与微观世界联系起来：𝑆= 𝑘 𝐵 𝑙𝑛 Γ 。其中 Γ 是可能状态的数量（与约束条件一致），𝑘 𝐵 是玻尔兹曼常数。因此，我们所要做的就是计算分子可能处于多少种状态，这就可以得出熵（从中可以得到所有其他热力学函数，如 F、G、H、Ω ）。因此，如果分子是已知的（因此它们的相互作用也是已知的，等等），那么就可以得到所有的热力学函数，并且可以预测所有材料在不同过程中的性质和行为。第二定律 ΔS 宇宙 > 0 是玻尔兹曼假设的必然结果，也是合乎逻辑的。很明显，这一定律完全是材料分子性质的结果。它解释了时间之箭，这是牛顿和量子力学基本自然定律中缺失的，这些定律表现出 t→-t 不变性（想象一下台球桌上两个球的碰撞——如果你倒着播放这部电影，你不会知道，因为牛顿定律仍然适用）。基于分子的工程设计。因此，统计力学提供了微观和宏观、分子世界和材料世界之间的联系。因此，它为现代分子工程时代打开了大门，这是化学工程的现在和未来的核心。统计力学使我们能够设计分子（甚至构建全新的分子，如聚合物），这些分子将构成具有所需特性的新材料，构建利用分子应用于传感和其他新技术的纳米级设备，或了解活细胞中的分子机制，从而指导疾病的治疗和预防。统计分析的计算技术。当然，统计力学是关于统计学。它是统计分析的科学，其概念和工具旨在分析和理解涉及大量变量的复杂随机过程。当今用于解决涉及大量变量的统计问题的计算方法库主要诞生于统计力学领域。如今，这些方法不仅用于分子系统的研究，还用于从大脑神经回路到人工智能再到数据科学的各种应用。
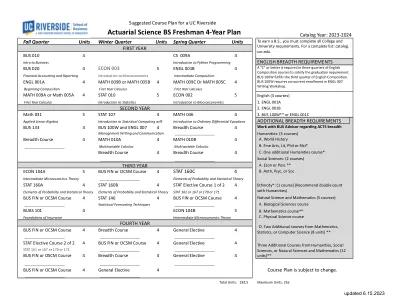
精算科学理学士 大一 4 年计划
中级微观经济学理论 _____________________ 概率论与统计理论要素 STAT 160A 4 STAT 160B 4 STAT 选修课 1/2 4 种族*:(1 门课程) (建议与人文学科双倍计算) 概率论与统计理论要素 概率论与统计理论要素 STAT 161 或 167 或 170 或 171 BUS FIN 或 OCSM 课程 4 STAT 146 4 BUS FIN 或 OCSM 课程 4 自然科学与数学(5 门课程)
情境测量模型与量子理论
量子概率论与经典概率论之间的相互关系是一个非常复杂的基础问题，涉及解释、数学和哲学问题。该领域的研究以观点、意见和数学形式主义的多样性为特点（例如[1–24]）。我们注意到，一般来说，量子力学（QM）的特点是具有多样性的解释。我个人的理解是，量子概率是一种概率更新机制，类似于经典贝叶斯推理[25–34]。与后者不同，量子概率推理不是基于条件概率的贝叶斯公式。量子概率论是一种概率推理理论，具有由投影或量子工具给出的一类特殊的概率更新变换。创建一个涵盖经典和量子概率的通用概率框架是很自然的。这种概括可以带来全球全景，因为从山顶可以欣赏整个城市的全景，并通过这个全景，将原本看起来完全分离的区域连接起来。这样，就更容易发现小区规划和建筑结构的相似点和不同点。作为概率更新的可能机器之一，量子概率形式主义将失去其神秘性。
PHY313a：“信息处理物理学”
模块 1：概率论回顾；随机系统和噪声；电磁场中的噪声 Shanon 信息简介；估计理论：Fisher 信息和 Cramer-Rao 界限；推理理论、Jayne 的解释、概率论的贝叶斯和频率论概念。（~7 周，14 堂讲座）模块 2：应用于经典、量子和统计力学的信息论：麦克斯韦妖、玻尔兹曼熵、热化、开放系统和噪声、冯·诺依曼熵。（~6 周，12 堂讲座）模块 3：应用和专题：电信技术要素和 Shanon 定理、量子信息论简介：不可克隆定理和量子密码学要素（~2 周，4 堂讲座）
模块 1 概率讲座 1-6 主题 1.1 ...
在我们的日常生活中，我们会遇到许多无法预测其性质的过程。此类过程称为随机过程。获取有关随机过程的信息的唯一方法是进行实验。每次这样的实验都会产生无法预测的结果。事实上，即使在相同条件下重复实验，由于存在无法控制的因素，实验结果也可能因试验而异。但是，我们可以提前知道实验的每个结果将导致几种给定可能性中的一种。例如，在固定环境下投掷骰子时，结果（骰子上表面的点数）无法提前预测，并且每次试验都会有所不同。但是，我们事先知道结果必须是数字 1、2、...、6 中的一个。概率论涉及随机过程的建模和研究。统计学领域与概率论密切相关，它涉及从与随机过程相关的数据中得出推论。
人工智能中不确定性的表示
摘要 由于人工智能主要关注知识表示和推理，它必然要处理各种处理不确定性的框架：概率论，以及更新的方法：可能性理论、证据理论和不精确概率。本章的目的是提供一个介绍性的概述，揭示表示不确定性的两个基本框架的具体特征：概率论和可能性理论，同时强调表示不确定性的任务所面临的主要问题。这一目的还提供了定位相关主题的机会，例如粗糙集和模糊集，它们分别受到考虑语言选择引起的表示粒度和自然语言谓词的渐进性的驱动。此外，本概述还简要介绍了其他理论表示框架，例如形式概念分析、条件事件和排名函数，以及可能性逻辑，与此处讨论的不确定性框架有关。本卷的下一章将讨论更复杂的框架：信念函数和不精确概率。
安德烈·阿加齐
2024 深度学习理论（比萨大学数学系博士课程）、数理统计（比萨大学数学系）、统计学 I（比萨大学工程系）、2023 概率论与统计学（比萨大学数学系）、统计学 I（比萨大学工程系）、2022 随机过程 (STA 210)（昆山杜克大学数学系）、概率论与统计学（比萨大学数学系）、统计学 I（比萨大学工程系）、2021 概率 (MATH 230)（杜克大学数学系）、统计学习理论 (STA 303)（昆山杜克大学数学系）、随机过程 (STA 210)（昆山杜克大学数学系）、2020 概率 (MATH 230)（数学系，杜克大学），随机微积分（MATH 545）（杜克大学数学系），毕业设计指导（杜克大学数学系），2019随机微积分（杜克大学数学系），
学士学位：信息工程 学习计划
微积分 1 12 计算机科学基础 12 英语语言 B2 3 线性代数 12 物理 1 12 数字系统 9 数据结构与算法 9 微积分 2 9 物理 2 9 概率论 9 信号与系统 9 电路 6 机器学习简介 6 电子学 9 电信 9 控制系统 9 期末考试 3