XiaoMi-AI文件搜索系统
World File Search System人工智能和正交性带来的生存风险:我们能两全其美吗?
Armstrong, S. (2014)。比我们更聪明。MIRI。Bostrom, N. (2002)。生存风险:分析人类灭绝情景和相关危害。《进化与技术杂志》,9,1-30。Bostrom, N. (2012)。超级智能意志:高级人工智能中的动机和工具理性。《思维与机器》,22(2 - 特别版“人工智能哲学”编辑。Vincent C. Müller),71-85。Bostrom, N. (2013)。生存风险预防是全球优先事项。全球政策,4 (1),15–31。https://doi。org/10.1111/1758-5899.12002 Bostrom, N. (2014)。超级智能:路径、危险、策略。牛津大学出版社。Bostrom, N.,& Ćirković, M. M.(Eds.)。(2011)。全球灾难性风险。牛津大学出版社。Cave, S. (2020)。智能问题:其价值历史和人工智能的未来。在 AIES '20:AAAI/ACM 人工智能、伦理和社会会议论文集(第29–35 页)。ACM。Chalmers,D. J.(2010)。奇点:哲学分析。《意识研究杂志》,17 (9–10),7–65。Drexler,E. K. (2019)。重新定义超级智能:综合人工智能服务作为通用智能。FHI 技术报告,2019-1, 1-210。https://www.fhi.ox.ac.uk/wp-content/uploads/Reframming_Superintelligence_FHI-TR-2019- 1.1-1.pdf Eden, A.、Moor, J. H.、Søraker, J. H. 和 Steinhart, E.(Eds.)。(2012)。奇点假设:科学与哲学评估 (The Frontiers Collection)。Springer。Fischer, J. M., & Ravizza, M. (2000)。责任与控制:道德责任理论。剑桥大学出版社。Fox, J., & Shulman, C. (2010)。超级智能并不意味着仁慈。在 K. Mainzer (Ed.中,ECAP10:第八届欧洲计算与哲学会议 (pp.1–7)。Dr Hut。Good, I. J.(1965)。关于第一台超智能机器的推测。在 F. L. Alt & M. Ruminoff (Eds.) 中,计算机的发展 (Vol.6 ,页31–88)。Academic Press。Häggström, O.(2016)。这里有龙:科学、技术和人类的未来。牛津大学出版社。Häggström, O.(2019)。对 Omohundro-Bostrom 人工智能动机框架的挑战。Foresight ,21 (1),153–166。https://doi.org/10.1108/FS-04-2018-0039 Häggström, O., & Rhodes, C.(Eds.)。(2019)。对人类的生存风险 (Foresight,Vol.21/1 )。Hofstadter, D. R. (1979)。哥德尔、埃舍尔、巴赫:永恒的金色辫子。基础书籍。康德,I.(1786)。道德形而上学的基础。牛津大学出版社。Kurzweil,R. (1999)。精神机器的时代:当计算机超越人类智能时。企鹅。Kurzweil, R. (2005)。奇点临近:当人类超越生物学时。维京人。Legg, S., & Hutter, M. (2007)。通用智能:机器智能的定义。心智与机器,17 (4),391–
物理学科学硕士.pdf
否积分:4单位I特殊功能:笛卡尔,圆柱形和球形极性坐标中Helmholtz方程的分离。Legendre函数:Legendre多项式,Rodrigue的公式;生成功能和递归关系;正交性和归一化;相关的Legendre功能,球形谐波。贝塞尔函数:第一类的贝塞尔函数,递归关系,正交性hermite函数:Hermite多项式,生成函数,递归关系;正交性。laguerre函数:laguerre和相关的Lauguerre多项式,递归关系;正交性。特殊功能在物理问题上的应用。10小时II单元矩阵:矢量空间和子空间,线性依赖性和独立性,基础和维度,革兰氏链式正交程序,正交,遗传学以及单位矩阵,特征值和特征值,eigenvectors,eigenvelors and eigenenvectors,ignalvelors of Matrices,diagonalization of Matrices,类似的物理化,应用程序,应用程序,应用于物理问题。积分变换:傅立叶变换:定义,傅立叶积分;逆变换;衍生物的傅立叶变换;卷积,parseval的定理;申请。拉普拉斯变换:定义,基本函数的变换,逆变换;派生的变换;变换的分化和整合;卷积定理;差分方程的解决方案;物理问题。物理中的张量。应用于分子光谱。10小时10小时单元III张量:线性空间,曲线坐标及其转换中的坐标转换;张量的定义和类型,逆转和协变量张量,对称和反对称张量,张量代数:平等,加法和减法,张量乘法,外产物;索引,内部产品,商定理,kronecker三角洲的收缩,张量的降低和升高,公制张量;基督教符号。10小时单位IV组理论:小组,子组和类;同构和同构,群体表示,可简化和不可约形的表示,Schur的引理,正交定理,表现形式,角色表的强度,将可还原的表现分解为不可减至的表征,代表性的构建,代表性的构建,谎言组,谎言组,旋转组,SO(2)等(3)。
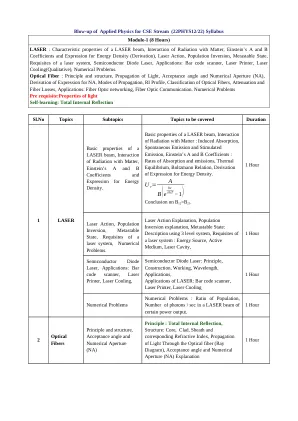
CSE 流应用物理学放大 (22PHYS12/22 ...
量子信息与量子计算原理:量子计算简介、摩尔定律及其终结、经典计算与量子计算之间的差异。量子比特的概念及其属性。布洛赫球对量子比特的表示。单量子比特和双量子比特。扩展到 N 量子比特。狄拉克表示和矩阵运算:0 和 1 状态的矩阵表示、恒等运算符 I、将 I 应用于 | 0 ⟩ 和 | 1 ⟩ 状态、泡利矩阵及其对 | 0 ⟩ 和 | 1 ⟩ 状态的运算、矩阵共轭 i) 和转置 ii) 的解释。酉矩阵 U、示例:行矩阵和列矩阵及其乘法(内积)、概率和量子叠加、规范化规则。正交性、正交性。数值问题量子门:单量子比特门:量子非门、泡利 - X、Y 和 Z 门、阿达玛门、相位门(或 S 门)、T 门多量子比特门:受控门、CNOT 门(针对 4 种不同输入状态的讨论)。交换门、受控 -Z 门、Toffoli 门的表示。
研究变分量子算法的可训练性
量子计算因其具有彻底改变计算能力的潜力而备受关注,随着它的出现,各种子领域的众多应用也应运而生。其中一个特别的子领域是量子神经网络 (QNN),它建立在流行且成功的经典对应物之上。QNN 通过利用量子信息中的量子力学原理和概念提供了一种替代方法。本论文项目研究变分量子算法作为量子神经网络的可训练性。具体而言,研究了用于天线倾斜优化用例的量子神经网络假设。QNN 架构在强化学习数据集上进行了测试,当仅实施单层时,其预测误差较低。此外,通过参数初始化技术检查了荒芜高原 (BP) 现象,该技术并没有改善模型的性能,因为添加了 QNN 的多层。最后,研究了训练数据集的结构,其中考虑了初始纠缠、线性独立性和正交性。研究发现,可控的纠缠量是有利的,没有纠缠或过多的纠缠会对模型的性能产生不利影响,而线性独立性和正交性的重要性高度依赖于数据集,线性独立性显示出进一步减少所需训练数据集大小的潜力。
可编程的哺乳动物翻译调节剂通过CRISPR相关蛋白
摘要合成遗传回路的复杂性依赖于具有高正交性的生物电路的曲目。尽管依赖RNA结合蛋白(RBP)的转录后电路符合曲目的资格,但监管设备的有限库阻碍了网络网络模块化和可扩展性。在这里,我们建议将墨盒(CAS响应转化调节可集成到多样化的基因组工程中)以将CRISPR相关(CAS)蛋白作为转化调节剂重新利用。我们证明了一组CAS蛋白能够抑制(OFF)或激活(ON)5'-UTR中包含CAS结合RNA基序的mRNA翻译。我们设计了81种不同类型的翻译,并在开关上验证了它们的功能特征。其中许多功能充当有效的翻译调节剂,并在哺乳动物细胞中显示正交性。通过互连这些开关,我们设计和构建了人工电路,包括60个翻译和大门。此外,我们表明,可以重新使用各种与CRISPR相关的技术,包括抗Crispr和Split-Cas9平台,以控制翻译。我们的CAS介导的翻译调节与CAS蛋白的转录调节兼容,并增加了元素较少的合成回路的复杂性。弹药筒比以往任何时候都更加构建蛋白质响应的mRNA开关,并导致CAS介导的基因组编辑和翻译调节技术的发展。
已发布版本的引文(APA):Müller, VC, & Cannon, M. (2022)。人工智能和正交性带来的生存风险:我们能两全其美吗?Ratio,35(1),25-36。https://doi.org/10.1111/rati.12320
• 已提交的稿件是文章提交后、同行评审前的版本。已提交的版本和正式出版的版本之间可能存在重大差异。建议对研究感兴趣的人联系作者获取出版物的最终版本,或访问出版商网站的 DOI。• 最终作者版本和样稿是同行评审后的出版物版本。• 最终出版版本包含论文的最终布局,包括卷、期号和页码。出版物链接
功能近红外光谱数据多维分解的并行因子分析
(HbO) 和脱氧 (HbR) 血红蛋白可以分别评估 HbO 和 HbR 的浓度变化。1 尽管 fNIRS 信号被认为对运动具有相对耐受性,2 但是由于运动伪影引起的光强度突然变化,数据质量可能会降低。3 结果表明,两种波长的动态特性为伪影检测和校正提供了重要信息。4 然而,当前用于运动伪影校正的技术(例如小波滤波、分解、样条插值等)通常假设两种波长的行为在时间上相似,因此无法利用两种波长提供的结构化信息。5 – 7 二维 (2D) 分析要求对具有更多维度的数据(例如 fNIRS 数据)在处理之前进行表面展开,例如分别处理两种波长或 HbO 和 HbR。因此,其中一些二维分析工具被迫施加其他非生理约束,例如主成分分析(PCA)中的正交性或独立成分分析(ICA)的统计独立性。尽管有几种方法可以实现 PCA,例如降维、分类、从信号分解的角度来看,PCA 旨在提取所谓的主成分,即可解释 fNIRS 中信号活动最大方差的成分。6、7、10、11 在时间 PCA 中,数据被分解为成分之和,每个成分由两个向量的乘积形成:一个代表时间主成分,另一个代表相应的地形(每个通道的分数)。PCA 的一个基本问题是仅由两个特征(时间和空间)定义的成分不是唯一确定的。因此,不同成分的对应时间特征之间必须具有正交性。 7、12、13然而,脑信号之间的正交性是一种非生理约束。即使有这种限制,提取的主成分也不是完全唯一的,因为任意旋转轴不会改变数据的解释方差。这导致研究人员使用不同的数学标准作为选择特定旋转的基础(例如,Varimax、Quartimax 和 Promax)。在 fNIRS 中,PCA 还被应用于目标时间间隔(tPCA),即仅在与发音或其他头部运动相关的伪影发生的期间,而不是在整个未分割的信号期间。3、14与基于小波的滤波和样条插值相比,这种类型的有针对性的校正可以产生更好的信号质量,同时也降低了改变信号整体完整性的风险。3虽然 PCA 非常常见且易于使用,一些作者已经讨论了其作为伪影校正方法的缺陷和注意事项。5、15
通过探索结构化视觉几何形状来表征简约中的3D视觉世界
艺术家使用这些原始阵列来描绘世界,展示他们捕捉环境本质的效力,从而创建清洁,完整和精确的内容。同样,作为人类,我们具有衡量维度和空间关系的能力,例如并行性和正交性,只有我们的视线。此功能使我们能够通过结构复杂的环境(如室内走廊和停车场)进行肯定地导航,并将我们的生活空间简化为具有象征性表示的地图,如图1。几何原始物的简单性和效率(包括点,线条,曲线和飞机)一直使我着迷,因为它们具有出色的能力,可以以一种简约的方式代表我们世界的复杂性。因此,我的研究受到了激励,我一直相信
Tesseract——高稳定性、低噪声磁通门传感器……
摘要。精确的高精度磁场测量对许多应用来说都是一项重大挑战,包括研究空间等离子体的星座任务。仪器稳定性和正交性对于在不进行大量交叉校准的情况下对星座中不同卫星进行有意义的比较至关重要。这里我们描述了 Tesseract 的设计和特性 - 一种专为低噪声、高稳定性星座应用而设计的磁通门磁强计传感器。Tesseract 的设计利用了定制低噪声磁通门芯制造方面的最新发展。六个定制的赛道磁通门芯牢固而紧凑地安装在一个坚固的三轴对称基座内。 Tesseract 的反馈绕组配置为四方 Merritt 线圈,以在传感器内部创建一个大的均匀磁零点,其中磁通门磁芯保持在接近零的磁场中,而不管环境磁场如何,以提高磁芯磁化循环的可靠性。 Biot-Savart 模拟用于优化反馈 Merritt 线圈产生的磁场的均匀性,并通过实验验证其沿赛道磁芯轴线的均匀性在 0.42 % 以内。使用线圈系统内装满干冰的绝缘容器来测量传感器反馈绕组的热稳定性。发现反馈绕组的温度灵敏度在 13 到 17 ppm ◦ C − 1 之间。传感器的三个轴在 −45 至 20 ◦C 的温度范围内保持正交性,误差不超过 0.015 ◦。Tesseract 的核心在 1 Hz 时实现了 5 pT √ Hz −1 的磁本底噪声。Tesseract 将在 ACES-II 探空火箭上进行飞行演示,目前计划于 2022 年底发射,并将再次搭载在 TRACERS 卫星任务上,作为 MAGIC 技术演示的一部分,目前计划于 2023 年发射。