XiaoMi-AI文件搜索系统
World File Search System玻色子
![arxiv：2105.10515v1 [Quant-ph] 2021年5月21日](/simg/d\d2995dfff70c7317a95e7b0782ee5b43bd0b8974.webp)
arxiv：2105.10515v1 [Quant-ph] 2021年5月21日
我们研究了在倾斜三孔电势中实验可访问的相互作用玻色子系统的量子古典对应关系。通过半经典分析，我们可以更好地了解量子系统的不同阶段，以及如何将它们用于量子信息科学。在可集成的极限中，我们对半经典哈密顿量的固定点的分析揭示了与二阶量子相变相关的关键点。在不可整合的域中，该系统表现出交叉。取决于参数和数量，最低能量状态的量子古典对应关系即使在很少的玻色子中也具有。我们讨论了如何探索不可整合模型的排斥性（有吸引力）相互作用区域中的这种状态以进行量子信息存储（量子传感）。
II型超导体中的通量量化...
摘要。本演示文稿探讨了电流涡流支撑的磁性和电孔管的物理，在具有超导状态的冷凝物质中，玻色子电荷载体在没有电阻的情况下流动。起点是玻色子波函数满足相对论量子力学的klein-gordon方程。接下来，假定超导介质内的电磁场服从用几何代数和微积分表达的绝对麦克斯韦方程，并结合了电或假设的磁电流。最后，计算的基本定理以两种形式使用来检查漏斗管，第一个在电气超导体中，然后在假设的磁性超导体中。几何代数和微积分能够对分析及其从三个空间维度进行一致的处理。
在室温下观察硝化氢硼中近红外亚poissonian光子发射
众所周知，连贯的光是可实现的最稳定的经典光，它表现出泊松统计分布。shot噪声代表了这种固有的随机性的极限，并与使用pois-sonian光源发射的光子的时间分离相关。因此，一个更正常或次佛森的光子流揭示了基础辐射过程的量子性质。1在任何给定时间发出不超过一个光子的完美常规光源，称为单光子源（SPS），代表了各种量子技术的必不可少的构建块，包括量子计算方案，玻色子计算方案，玻色子采样，精确的Metrology，Precision Metrology，以及安全的通信应用以及量子密钥分布，例如量子密钥分布。2–6
Kapitel 2第二量化简介
现在，我们转向处理量子N粒子系统的不同方法。，而不是首先用两个规范上的构造理论构建经典的场理论，这些场量正在量化第二步，我们现在进行了不同。我们将从玻色子（Fermions）的情况下对许多颗粒的状态的量子机械描述开始。然后，我们基于引入创意和歼灭操作员的引入，转换为量化相当微不足道的职业编号表示。该方案将在第3章中实现Fermions和Bosons。，但在此之前，考虑经典粒子极限的类似多体问题并执行“相空间中的第二个量化”是非常具有启发性的。这是通过引入归功于Klimontovich，CF的微观相空间密度来实现的。等式。 （2.13）以下。 我们将观察到，该数量遵守一个完全类似于将在SEC中得出的费米和玻色子的运动算子的运动方程式的运动方程。 5.2。 这允许对第二个量化的常见统计概念有宝贵的见解。等式。（2.13）以下。我们将观察到，该数量遵守一个完全类似于将在SEC中得出的费米和玻色子的运动算子的运动方程式的运动方程。5.2。这允许对第二个量化的常见统计概念有宝贵的见解。
对聚焦的广义Hartree方程
，例如，可以将其视为在非相关环境中多体量子系统的模型；这也是在分子之间的远距离相互作用的研究中产生的。多体量子系统的均值限制的工作，其中玻色子的数量很大，但是它们之间的相互作用很弱，也可以追溯到HEPP [30]，也可以参见[58]，[9]，[8]，[18]，[18]。lieb and Yau [42]在Chandrasekhar的恒星崩溃理论的背景下提到了这一点，该理论说，在恒星死亡之后，取决于其质量，恒星残余物可以采取三种形式之一：中子恒星，白矮人和黑洞。lieb and thirring [41]猜想玻色子星的倒塌可以通过hartree型方程来预测。R 3中的γ= 2的Riesz电位的特殊情况为
相干态的乌尔曼相和乌尔曼-贝里对应关系
Berry相[1]通过绝热循环过程后获得的相位揭示了量子波函数的几何信息，它的概念为理解许多材料的拓扑性质奠定了基础[2–13]。Berry相理论建立在纯量子态上，例如基态符合零温统计集合极限的描述，在有限温度下，密度矩阵通过将热分布与系统所有状态相关联来描述量子系统的热性质。因此，将Berry相推广到混合量子态领域是一项重要任务。已有多种方法解决这个问题[14–21]，其中Uhlmann相最近引起了广泛关注，因为它已被证明在多种一维、二维和自旋j系统中在有限温度下表现出拓扑相变[22–26]。这些系统的一个关键特征是 Uhlmann 相在临界温度下的不连续跳跃，标志着当系统在参数空间中穿过一个循环时，底层的 Uhlmann 完整性会发生变化。然而，由于数学结构和物理解释的复杂性，文献中对 Uhlmann 相的了解远少于 Berry 相。此外，只有少数模型可以获得 Uhlmann 相的解析结果 [ 22 – 30 ] 。Berry 相是纯几何的，因为它不依赖于感兴趣量子系统时间演化过程中的任何动力学效应 [ 31 ] 。因此，Berry 相理论可以用纯数学的方式构建。概括地说，密度矩阵的 Uhlmann 相是从数学角度几乎平行构建的，并且与 Berry 相具有许多共同的几何性质。我们将首先使用纤维丛语言总结 Berry 相和 Uhlmann 相，以强调它们的几何特性。接下来，我们将给出玻色子和费米子相干态的 Uhlmann 相的解析表达式，并表明当温度趋近于零时，它们的值趋近于相应的 Berry 相。这两种相干态都可用于构造量子场的路径积分 [32 – 37]。虽然单个状态中允许有任意数量的玻色子，但是泡利不相容原理将单个状态的费米子数限制为零或一。因此，在玻色子相干态中使用复数，而在费米子相干态中使用格拉斯曼数。玻色子相干态也用于量子光学中，以描述来自经典源的辐射 [38 – 41]。此外，相干态的Berry相可以在文献[ 42 – 45 ]中找到，我们在附录A中总结了结果。我们对玻色子和费米子相干态的 Uhlmann 相的精确计算结果表明，它们确实携带几何信息，正如完整概念和与 Berry 相的类比所预期的那样。我们将证明，两种情况下的 Uhlmann 相都随温度平稳下降，没有有限温度跃迁，这与先前研究中一些具有有限温度跃迁的例子形成鲜明对比 [ 22 – 30 ] 。当温度降至零度时，玻色子和费米子相干态的 Uhlmann 相接近相应的 Berry 相。我们对相干态的结果以及之前的观察结果 [ 22 , 24 , 26 ] 表明，在零温度极限下，Uhlmann 相还原为相应的 Berry 相。
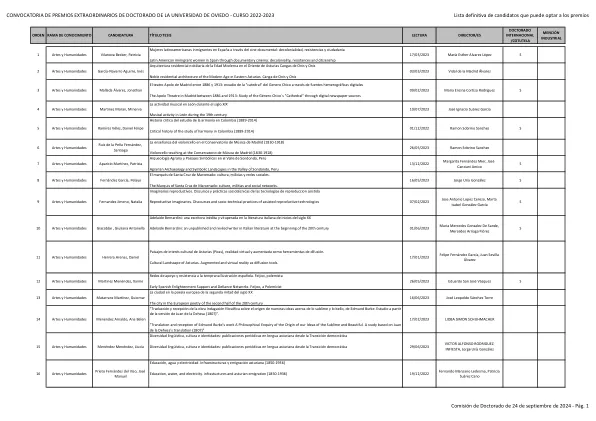
课程2022-2023候选人确定清单
测量包含的和差分横截面，用于单个顶级夸克产生，与质子 - 普罗顿碰撞中的W玻色子相关，√s= 13 TEV 21/04/2023IsidroGonzálezCaballero，Barbara
![arXiv:2108.00923v1 [hep-ph] 2021 年 8 月 2 日](/simg/5\5d0cdb6c8bc3490594c71f277ccbb0c70ba334ad.webp)
arXiv:2108.00923v1 [hep-ph] 2021 年 8 月 2 日
长期以来，各种理论模型都预测了分子态，特别是在单玻色子交换模型中预测的 DD ∗ 同标量轴矢量分子态。在本文中，我们研究了高斯展开法中的 DDD ∗ 系统，其 DD ∗ 相互作用源自单玻色子交换模型，并受到 T cc 相对于 D ∗ + D 0 阈值的 273 ± 63 keV 的精确结合能约束。我们证明了 DDD ∗ 态的存在，其结合能为几百 keV，自旋宇称为 1 − 。其主要衰变模式是 DDD π 和 DDD γ 。这种状态的存在原则上可以通过即将发布的 LHC 数据得到证实，并将明确地确定 T + cc 态以及许多类似奇异状态的性质，从而加深我们对非微扰强相互作用的理解。
纠缠辅助量子安全隐蔽通信
隐蔽通信或低检测/拦截概率 (LPD/LPI) 通信可以防止对手检测到传输。与标准方法（例如量子密钥分发 (QKD)）提供的保护传输内容免遭未经授权的访问相比，这是一种更严格的安全要求。在这里，我们重点介绍图 1 所示的热噪声有损玻色子通道上的量子安全隐蔽通信。玻色子通道是光通道的量子力学描述，其参数为发射器 Alice 和预期接收器 Bob 之间的透射率 η，以及热环境注入的每种模式的平均光子数 ¯ n B，其中单个时空偏振模式是我们的基本传输单元。Alice 的目标是可靠地将数据传输给 Bob，即以任意小的解码错误概率。这必须隐蔽地完成：确保对手 Willie 可以构造的任何检测器都接近随机猜测。
观察WWγ的产生并搜索Hγ...
提出了质子质子碰撞中WWγ产生的观察，在13 TEV的质量中心能量中，呈综合光度为138 fb-1。观察到的（预期）显着性为5.6（5.1）标准偏差。是通过需要两个相反电荷的两个lept子（一个电子和一个muon），中度缺失的横向动量和一个光子来选择事件。WWγ的测得的基准横截面为5。9 0。8ðstatþ0。8ðsystÞ0。7ð建模fb，与次级别量子量子染色体动力学预测一致。通过搜索Higgs玻色子和光子的相关产生进行扩展分析，这是由Higgs Boson与Light Quarks的耦合产生的。该结果用于将希格斯玻色子耦合限制为列夸克。