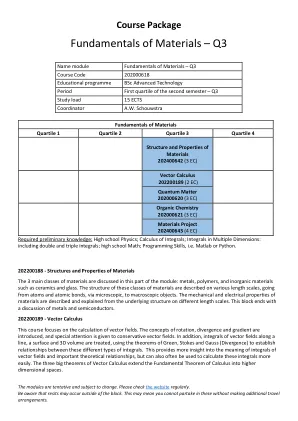
XiaoMi-AI文件搜索系统
World File Search System积分的
瓦朗加尔国立科技学院
PO1 PO2 PO3 PO4 PO5 PO6 CO1 3 3 2 2 2 3 CO2 3 2 2 3 3 2 CO3 3 2 3 3 2 3 CO4 3 3 3 3 2 3 教学大纲： 基础拓扑：简介 黎曼斯蒂尔杰积分：积分的定义和存在性，积分的性质，具有可变极限的积分的积分和微分。 不正确积分：定义及其收敛性，收敛测试， 和 函数。 一致收敛：一致收敛的测试，和函数的极限和连续性定理，函数级数的逐项微分和积分。 幂级数：收敛及其性质。 傅里叶级数：狄利克雷条件、存在性、问题、半程正弦和余弦级数。学习资源：教科书：1. 数学分析原理，Walter Rudin，McGraw Hill，2017，第三版。2. 实分析，Brian S.Thomson，Andrew M.Bruckner，Judith B.Bruner，Prentice Hall
![arxiv：2503.00261v1 [Math.ca] 2025年3月1日](/simg/g:\will\search\icon\source\5\51260f1baf682b036f8d38e1c4a3d438c1269b51.webp)
arxiv：2503.00261v1 [Math.ca] 2025年3月1日
获得与L相关的分数积分的定量矩阵加权估计值，一个自然的理想是在[3，4]中采用这个想法，以稀疏操作员在本地部分中占主导地位，并由最大操作员统治全球部分，但是，与标量相比，与标量相比，与量表相比，又一次的态度并不是一个损失的对象，而不是构成对象，而不是对象，而是对象的构成，则是对对象的构成。这阻止了我们在[3，4]中使用该技术。此外，操作员还有其他临界半径功能因子。因此，以下问题是自然的。问题1：如何获得变形型积分的定量矩阵加权估计值？此外，由更一般的差异操作员替换Schréodinger运营商L，我们可能会面临新的挑战，因为-L产生的半群的内核不能满足任何规律性条件。接下来，即将到来的问题是我们处理的矩阵权重类。根据定理1.2中的权重类别，可能需要新的矩阵权重。问题2：在L的环境中，分别适合于定量矩阵加权估计值和分数类型积分的两重量不平等的矩阵重量和凸起的con。如果存在新的权重，则如何处理这些类别的矩阵权重以获得所需的结论？我们可以找到这些类矩阵权重的一些特征吗？最后，与备注1.6有关，我们还猜想了与L相关的分数积分仍然是正确的。但是，我们认为证明这种猜想还有很长的路要走。问题3：在我们的新环境中，我们可以迈出证明这一猜想的道路吗？
（信息技术）
数学逻辑：命题逻辑；一阶逻辑：概率：条件概率；卑鄙，中位数，模式和标准偏差；随机变量；分布；制服，正常，指数，泊松，二项式。集合理论与代数：集合，关系，功能，群体，部分订单，晶格，布尔代数。组合学：排列，组合，计数，求和，生成功能，复发关系，渐近学。图理论：连通性，跨越树，切割的顶点和边缘，覆盖，匹配，独立集，着色，平面性，同构。线性代数：矩阵的代数，决定因素，线性方程系统，本特征值和本本矢量。数值方法：线性方程系统的LU分解，通过secant，bisection和Newton-Raphson方法的非线性代数方程的数值解；梯形和辛普森规则的数值集成。微积分：极限，连续性和不同性，平均值定理，积分的定理，确定和不当积分的评估，部分衍生物，总导数，Maxima＆Minima。
（计算机科学）
1。工程数学数学逻辑：命题逻辑；一阶逻辑：概率：条件概率；卑鄙，中位数，模式和标准偏差；随机变量；分布；制服，正常，指数，泊松，二项式。集合理论与代数：集合，关系，功能，群体，部分订单，晶格，布尔代数。组合学：排列，组合，计数，求和，生成功能，复发关系，渐近学。图理论：连通性，跨越树，切割的顶点和边缘，覆盖，匹配，独立集，着色，平面性，同构。线性代数：矩阵的代数，决定因素，线性方程系统，本特征值和本本矢量。数值方法：线性方程系统的LU分解，通过secant，bisection和Newton-Raphson方法的非线性代数方程的数值解；梯形和辛普森规则的数值集成。微积分：极限，连续性和不同性，平均值定理，积分的定理，确定和不当积分的评估，部分衍生物，总导数，Maxima＆Minima。
赚取COVID-19疫苗接种的积分
随着COVID-19疫苗变得越来越广泛，很明显，它将是帮助阻止病毒传播的关键工具。考虑到这一点，我们很高兴能为选择接种疫苗的成员获得500个活力积分的疫苗接种 - 每种接种剂量的剂量为250。