XiaoMi-AI文件搜索系统
World File Search System7100积分版本可在以下链接
申请表将由法官委员会审查,该委员会专门由校长任命(有关委员会的组成第2段)。委员会在提出申请的截止日期以来的二十天之内,并有合理的报告,将根据提出的学术和科学资格的选择以及旨在验证候选人对所需语言的研究和知识的旨在验证旨在验证候选人的能力的采访。委员会首先建立评估标准,并评估候选人最多可以使用100分,50分,用于以下方式分配的资格:
Nesterov型加速度方法的快速符号积分器
摘要在本文中,为在提高Nesterov加速梯度方法的收敛速率时,提出了基于符号和接触差异的显式稳定积分器。符合性几何形状适用于描述Ham-iLtonian力学,接触几何形状被称为奇异的几何形状。一种称为符合性的程序是一种已知的方法,可以从触点歧管中构建符号歧管,从接触膜构造自动式哈密顿系统。在本文中发现,先前研究的非自主odes可以写为汉密尔顿系统家庭。然后,通过开发和应用表达非自主odes的非自主接触的符合性,并实现了新型的符号积分。由于所提出的符号积分器保留了ODES中隐藏的符号和接触结构,因此预计它们比Runge -Kutta方法更稳定。数值实验表明,正如预期的那样,二阶符号积分器是稳定的,并且达到了高收敛速率。
基于积分的系统赞助商许可:应用程序
•他们的组织详细信息•他们提交的支持文件•一旦接受在线付款并以电子方式提交申请,申请人将收取的费用详细信息发送给提交表并直接将文件发送给赞助商许可单位。收到提交表和任何支持文档后,工作流团队在日期订单中提交了该案例,准备案例工作者将其与电子案例匹配。案例,以查看它们是直接,复杂的还是应拒绝,或者在向案例工作者提供之前应被拒绝。官方 - 敏感:开始本节中的信息已被删除,因为它仅限于内部家庭办公室使用。
241107-01 主题:积分管理案例创建...
适用于:空军国民警卫队和空军预备役飞行员 BLUF:HQ ARPC 积分管理在直接创建 myFSS 案例时遇到技术困难。用户尝试通过 AFR/ANG 通用积分信用信息知识文章(答案 ID:000008063)或从案例创建菜单中选择“ARC-积分管理-积分正确”为积分管理创建案例可能会遇到错误。这是一个已知问题,目前正在解决。我们没有修复 myFSS 错误的预计时间表。替代案例提交:仍然可以通过 myFSS 登录页面上的“提问”链接将案例提交给积分管理。请按照以下步骤确保您的案例及时分配到正确的队列:
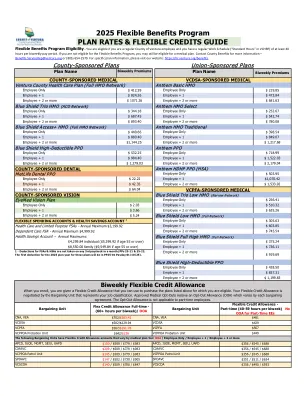
2025 年灵活福利计划计划费率和灵活积分指南灵活福利计划资格 - 如果您是常规伯利兹伯利兹居民,则您有资格
2025 年灵活福利计划计划费率和灵活积分指南灵活福利计划资格 - 如果您是文图拉县的普通员工,并且每两周工资期有至少 40 小时的固定工作时间(VCHRP 中的“标准工作时间”),则您符合资格。如果您不符合灵活福利计划的资格,您仍可能有资格享受医疗计划。请联系县福利部门了解更多信息 - Benefits.ServiceRep@ventura.org 或 (805) 654-2570。有关具体计划信息,请访问我们的网站:https://hr.ventura.org/benefits。
数学 311 – 微积分 III – 教学大纲
另一个。• 找到空间中直线的参数和对称方程。• 找到空间中两个物体之间的距离。• 识别空间中的表面。• 确定矢量值函数的极限、连续性、导数和积分。• 使用向量解决涉及速度、力和功的应用问题。• 确定矢量值函数的曲率。• 找到矢量值函数的单位切向量、法向量和副法向量
使用光流>对路径积分的控制和重新校准
海马位置细胞受到自我运动(白痴)信号和外部感觉地标的影响,因为动物会导航其环境。为了不断更新内部“认知图”上的位置信号,海马系统会随着时间的推移整合了自我运动信号,该过程依赖于精细校准的路径积分增益,该过程将物理空间中的运动与认知图上的运动相关。目前尚不清楚单独使用习惯性提示(例如光流)是否对认知图产生足够的影响以实现路径积分的重新校准,还是地标提供的偏振位置信息对于此重新校准至关重要。在这里,我们通过自由移动的大鼠中的纯光流信息进行了路径积分增益的重新校准和对位置的系统控制。这些发现表明,大脑不断地重新平衡冲突的惯用性线索的影响,以微调路径整合的神经动力学,并且这种重新启动过程不需要自上而下的,明确的位置信号。
指数积分器中线体函数的方向分裂...
vec是将输入矩阵的列堆叠在单个向量中的操作员。具有Kronecker和结构的系统在应用线路方法上近似于在张量产品域和适当的边界条件上定义的部分微分方程(PDE)的解时,通常也会出现。的确,在众所周知的抛物线方程(例如Allen-Cahn,Brusselator,Gray-Scott,Advection-Affection-Exfusion-Reaction [8,10]或Schrödinger方程[6])的空间中,我们获得了ODES的大僵硬系统(1)。一旦给出了系统(1),就可以使用许多技术来及时整合它,尤其是我们对指数积分器的应用感兴趣[19]。实际上,它们是执行所需任务的重要方法,因为它们享有有利的稳定性,使它们适合在僵硬的制度中工作。这些方案需要计算矩阵指数和向量上的指数状矩阵函数(所谓的线体函数)的作用。它们是定义的,对于通用矩阵x∈Cn×n,为