XiaoMi-AI文件搜索系统
World File Search System自主电力系统中混合电能存储系统参数识别
1. 引言 目前,电能存储系统 (EESS) 被广泛用于解决电力工业的各种问题。近几十年来,储能技术的密集发展导致了具有特性 (功率、能量强度、效率系数、速度) 的 EESS 的诞生,这些特性 (功率、能量强度、效率系数、速度) 使项目能够以技术和经济效率实施。2017 年,俄罗斯联邦能源部批准了《俄罗斯联邦电力存储系统市场发展构想》[1]。此外,能源计划还指出了在俄罗斯联邦能源领域引入储能系统的具体任务,该计划是国家技术倡议的长期综合计划的一部分,旨在到 2035 年形成全新的市场并为俄罗斯在全球技术领导地位创造条件 [2]。现代快速 EESS 是一种全新的能源电力设备,旨在与电力系统进行受控的能量交换,以组织所需的模式或控制动态过程。EESS 能够根据任何给定的算法几乎立即控制有功功率平衡。根据给定的任务,EESS 可用作无功功率补偿装置、高次谐波有源滤波器以及三相网络不对称补偿手段。由于 EESS 技术的新颖性,其在俄罗斯电力工业实践中的开发和实施始于相对较小的额定功率和能量强度。俄罗斯联邦的自主能源系统中有许多 EESS 项目可供实施,这些项目具有较高的经济和技术效率。受控能量交换过程中的功率变化速度由 EESS 的功能目的决定。目前最相关的储能设备类型是:锂离子电池和超级电容器。第一种类型对于相对较慢的过程最有效,而第二种类型对于较慢的过程最有效。
EMBRAER 135-145 - 机组人员意识 - 捷特航空 X
多功能显示器 (MFD) 提供雷达、TCAS、FMS、CMC 和其他导航信息和系统页面。有五个系统页面可用: − 燃油:提供燃油系统参数和状态。 − 电气:提供电气系统参数和状态。 − 环境和防冰:提供空调、气动、氧气和防冰防雨系统参数和状态。 − 液压和刹车:提供液压和刹车系统和状态。 − 起飞:提供起飞温度设置、油位和舱门状态。有关系统页面的更多信息,请参阅每个相关系统描述。
2021 年联邦无线电导航计划 - navcen
6.3 可互换解决方案 ................................................................................................ 6-6 6.4 PNT 与通信的协同作用 ................................................................................ 6-6 6.5 合作组织结构 ................................................................................................ 6-7 6.6 展望未来 ........................................................................................................ 6-8 附录 A. 系统参数和说明 ............................................................................................. A-1 A.1 系统参数 ............................................................................................................. A-1 A.1.1 信号特性 ............................................................................................. A-1 A.1.2 精度 ............................................................................................................. A-1 A.1.3 可用性 ............................................................................................. A-3 A.1.4 覆盖范围 ............................................................................................. A-3 A.1.5 可靠性 ............................................................................................. A-3 A.1.6 定位速率 ............................................................................................. A-3 A.1.7 定位尺寸 ............................................................................................. A-3 A.1.8 系统容量 .............................................................................................
2021 年联邦无线电导航计划 - navcen
6.3 可互换解决方案 ................................................................................................ 6-6 6.4 PNT 与通信的协同作用 ................................................................................ 6-6 6.5 合作组织结构 ................................................................................................ 6-7 6.6 展望未来 ........................................................................................................ 6-8 附录 A. 系统参数和说明 ............................................................................................. A-1 A.1 系统参数 ............................................................................................................. A-1 A.1.1 信号特性 ............................................................................................. A-1 A.1.2 精度 ............................................................................................................. A-1 A.1.3 可用性 ............................................................................................. A-3 A.1.4 覆盖范围 ............................................................................................. A-3 A.1.5 可靠性 ............................................................................................. A-3 A.1.6 定位速率 ............................................................................................. A-3 A.1.7 定位尺寸 ............................................................................................. A-3 A.1.8 系统容量 .............................................................................................
用户手册 - / 索引
概述 ................................................................................................................7-1 配置 ................................................................................................................7-3 步骤 1,启动向导 ..............................................................................................7-3 步骤 2,系统参数 ..............................................................................................7-3 步骤 3,通道设置 .............................................................................................7-4 步骤 4,中心站点同步设置 .............................................................................7-8 步骤 5,服务 ......................................................................................................7-8 步骤 6,TDM 时钟配置 ......................................................................................7-9 步骤 7,配置摘要和退出 .............................................................................7-10
华为Smartli 3.0 ST DataSheet 03- (20221228).pdf
•显示电池系统的总电压,SOC,SOH,电流和温度以及每个电池柜的电池信息。•接收每个BCU报告的常见参数并保存本地数据。•收到BCU报告的警报和保护事件,并在当地保存事件。•与UPS进行通信,为本地和远程操作提供人机交互,通信端口和许可管理,设置电池管理系统参数并升级程序。
模块可再生能源和能源效率基础...
本模块的内容向学员介绍了可持续建筑电力供应中混合可再生能源(光伏太阳能、风能)的尺寸确定,以及它们在配电系统中的集成。将开展案例研究,以更好地理解这些技术。此外,学员将学习使用 HOMER 软件根据不同的能源(可再生能源、混合系统)设计和确定分布式发电 (DG) 系统的规模。我们将使用该软件模拟不同类型的系统,在技术和经济上对其进行优化,并对系统参数进行敏感性分析。
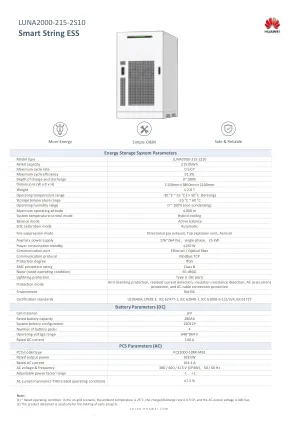
luna2000-215-2S10-智能字符串ESS
能源存储系统参数类型类型LUNA2000-215-2S10额定容量215.0kWh最大周期速率0.5 CP最大周期效率91.3%充电和排放的深度0〜100%尺寸(W x D x H)1150mm×1800mm×1800mm×2100mm×2100mm重量; 〜60°C运行湿度范围0〜100%(无调)最大工作高度4,000 m系统温度控制模式混合冷却平衡模式主动平衡SOC校准模式自动
太阳能热化学制氢系统及技术经济分析
Co 0.1 Fe 0.9 Al 2 O 4 [28] 174.1 2.08 1,450 < 400 250 Mn 0.5 Fe 0.5 Al 2 O 4 [28] 173.4 1.38 1,450 < 400 340 La 0.6 Sr 0.4 MnO 3 [29] 221.3 3.80 1,400 < 600 650 † CeO 2 [34] 172.1 7.00 ‡ 1,500 ~700 130 分析基线 - 4.00 - - 200 * T TR 和温度波动是近似值,取决于各种系统参数。† 可能实现的生产率。‡ 铈的成本逐年波动很大;选择了中等价格。