XiaoMi-AI文件搜索系统
World File Search System人工智能中的线性代数
*对于处于数字化转型阶段的组织而言,敏捷性是应对快速变化的技术和商业环境的关键。现在比以往任何时候都更重要的是,以创新为后盾的强大数字思维来实现并超越组织的期望。让企业能够像生物体一样感知、学习、响应和发展,对于实现卓越业务至关重要。一套全面而模块化的服务正是在做到这一点。Live Enterprise 为组织提供直观的决策能力,自动进行大规模决策,基于实时解决方案的可行洞察,随时随地的体验,以及跨职能部门的深入数据可视性,从而实现超高生产力,从而构建互联的组织,共同创新,迎接未来。
线性代数的机器学习方法
机器学习是一门编程科学,让机器像人类一样思考和行动,而无需专门编程。我们在日常生活中已经不知不觉地使用了机器学习。垃圾邮件识别、拼写检查,甚至带你到这里的 YouTube 视频推荐都是使用机器学习实现的。机器学习使用算法来学习任务,这些算法以数据为输入,它们学习执行这些任务。这意味着随着时间的推移,当数据发生变化时,我们不需要重新编程我们的应用程序,只需让它找到模式并从新数据中学习。机器学习是人工智能的一个子集,人工智能是一门科学,旨在将类似人类的智能赋予机器,并创造一种能够感知、推理、行动、适应的机器。深度学习是机器学习的一个分支,其灵感来自人类大脑的工作方式。机器学习正引领我们走向一个机器可以学习和思考的未来。机器学习中的模型选择是针对特定问题选择最适合模型的过程。选择模型取决于各种因素,例如数据集、任务、模型的性质等。
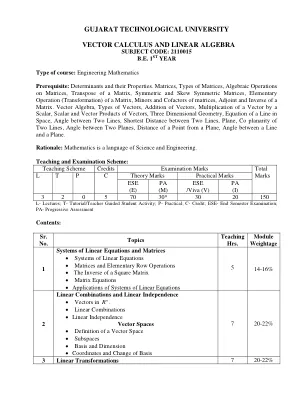
MATH 361 线性代数
本课程介绍有限维抽象向量空间和线性变换的理论。主题包括:线性方程组、矩阵、矩阵代数、行列式和逆、线性组合和线性独立性、抽象向量空间、基和坐标变换、内积空间、正交基。我们还考虑线性变换、同构、线性映射的矩阵表示、特征值和特征向量、对角化和相似性。应用包括计算机图形学、马尔可夫链、化学、线性回归、网络流、电路和微分方程。
经济地理模型的线性代数
摘要 我们提供了恒定弹性经济地理模型中名义和实际工资对生产力冲击暴露的充分统计数据。这些暴露指标总结了每个地点名义和实际工资对所有地点生产力冲击的一阶一般均衡弹性。它们可以使用常见的贸易数据以及贸易和移民弹性值轻松计算。它们在底层经济机制方面具有直观的解释。计算所有双边位置对的这些度量涉及单个矩阵求逆,因此即使在极高维状态空间中仍保持计算效率。这些充分的统计数据提供了理论一致的地点对生产力冲击暴露的度量,可用于进一步的经济和统计分析。关键词:经济地理、贸易、移民 JEL:F10;F15;R12 我们感谢普林斯顿大学的研究支持。我们要感谢张晨明提供的出色研究协助。本文是为《美国经济评论》论文集和会议记录准备的。适用通常的免责声明。
量子计算的线性代数
正则化向量或单位向量是范数等于 1 的向量。如果所有向量都是正则化的并且相互正交,则称基是正交的。具有内积的有限向量空间称为希尔伯特空间。为了使无限向量空间成为希尔伯特空间,它除了具有内积之外,还必须遵循其他属性。由于我们主要处理有限向量空间,因此我们使用术语希尔伯特空间作为具有内积的向量空间的同义词。有限希尔伯特空间 V 的子空间 W 也是希尔伯特空间。与 W 的所有向量正交的向量集是希尔伯特空间 W - 称为正交补。V 是 W 和 W - 的直接和,即 VDW˚W-。N 维希尔伯特空间将用 HN 表示以突出其维数。与系统 A 相关的希尔伯特空间将用 HA 表示。
线性代数:本质与形式
数学是现代工程的语言,线性代数是其美国方言——不雅、实用、无处不在。本书旨在帮助工程专业的学生为人工智能、数据科学、动力系统、机器学习和其他领域的数学方面做好准备,这些领域的进步主要依赖于线性代数方法。读者在读本书时至少在微积分课程中接触过矩阵和向量。这些工具虽然已经作为计算设备为人们所熟悉,但它们包含值得仔细研究的更深层次的结构。我们的任务是在此计算能力的基础上,理解使现代工程方法成为可能的抽象框架。本书在重点和节奏上与标准线性代数课程不同。抽象向量空间出现较早,但始终服务于具体应用。奇异值分解和特征理论——对现代实践至关重要——到达了中间点,允许扩展动力学和数据科学中的应用。书中贯穿着实际例子,表明理论理解和实用实施是对称的。主题顺序平衡了教学必要性和当代相关性。线性方程组提供了一个切入点,通向向量空间和线性变换。内积和正交性构建了几何直觉,线性微分方程和迭代系统为特征分解提供了动力。奇异值分解既是理论的巅峰,也是通往强大应用的桥梁,例如主成分分析、低秩近似和神经网络。本书的存在是因为工程教育必须发展。虽然线性代数的基础保持稳定,但它们的应用却急剧扩展。今天的工程学生需要掌握抽象理论和实际实施——不仅仅是应用现有的工具,还要创造新的工具。线性代数不是终点,而是迈向更深层次数学结构的第一步。我们正是通过这个视角来探讨这个问题:作为当前实践和未来进步的门户。
量子数值线性代数简介
▶ 因式分解 ▶ 非结构化搜索 ▶ 离散傅里叶变换 ▶ 应用数学:线性系统,微分方程,最优化,机器学习,· · · 量子算法动物园:https://quantumalgorithmzoo.org 林林的讲义:[arXiv:2201.08309]