XiaoMi-AI文件搜索系统
World File Search System用于计算机视觉,机器人技术和机器学习的线性代数
近年来,计算机视觉,机器人技术,机器学习和数据科学一直是一些为技术取得重大进展做出贡献的关键领域。任何在上述领域看论文或书籍的人都将被一个奇怪的术语所付诸实践,其中涉及异国情调的术语,例如内核PCA,脊回归,套索回归,支持向量机(SVM),Lagrange乘数,KKT条件等。支持向量机可以追赶牛以某种超级套索抓住他们吗?不!,但是人们会很快发现,在术语后面,总是带有新的场(也许是为了使局外人远离俱乐部),这是许多“经典”线性代数和优化理论中的技术。是主要的挑战:为了了解和使用机器学习,计算机视觉等的工具,需要在线性代数和优化理论中具有企业背景。老实说,还应包括一些概率理论和统计数据,但我们已经有足够的能力与之抗衡。许多有关机器学习的书籍与上述问题。如果一个人不了解拉格朗日二元框架,那么一个人如何忍受脊回归问题的双重变量是什么?同样,如何在不了解拉格朗日框架的情况下讨论SVM的双重公式?简单的出路是将这些困难范围扫到地毯下。如果只是我们上面提到的技术的消费者,那么食谱食谱方法可能就足够了。这些包括:但是,这种方法对真正想进行认真研究并做出重要贡献的人不起作用。要这样做,我们认为一个人必须具有线性代数和优化理论的坚实背景。这是一个问题,因为这意味着要投入大量时间和精力研究这些领域,但我们认为毅力将得到充分的回报。我们的主要目标是介绍线性代数和优化理论的基础,请注意机器学习,机器人技术和计算机视觉的应用。这项工作由两卷组成,第一卷是线性代数,第二个是一种优化理论和应用,尤其是用于机器学习。这首卷涵盖了“经典”线性代数,直至主要构成和约旦形式。除了涵盖标准主题外,我们还讨论了一些对应用程序重要的主题。
用于计算机视觉,机器人技术和机器学习的线性代数
近年来,计算机视觉,机器人技术,机器学习和数据科学一直是一些为技术取得重大进展做出贡献的关键领域。任何在上述领域看论文或书籍的人都将被一个奇怪的术语所付诸实践,其中涉及异国情调的术语,例如内核PCA,脊回归,套索回归,支持向量机(SVM),Lagrange乘数,KKT条件等。支持向量机可以追赶牛以某种超级套索抓住他们吗?不!,但是人们会很快发现,在术语后面,总是带有新的场(也许是为了使局外人远离俱乐部),这是许多“经典”线性代数和优化理论中的技术。是主要的挑战:为了了解和使用机器学习,计算机视觉等的工具,需要在线性代数和优化理论中具有企业背景。老实说,还应包括一些概率理论和统计数据,但我们已经有足够的能力与之抗衡。许多有关机器学习的书籍与上述问题。如果一个人不了解拉格朗日二元框架,那么一个人如何忍受脊回归问题的双重变量是什么?同样,如何在不了解拉格朗日框架的情况下讨论SVM的双重公式?简单的出路是将这些困难范围扫到地毯下。如果只是我们上面提到的技术的消费者,那么食谱食谱方法可能就足够了。这些包括:但是,这种方法对真正想进行认真研究并做出重要贡献的人不起作用。要这样做,我们认为一个人必须具有线性代数和优化理论的坚实背景。这是一个问题,因为这意味着要投入大量时间和精力研究这些领域,但我们认为毅力将得到充分的回报。我们的主要目标是介绍线性代数和优化理论的基础,请注意机器学习,机器人技术和计算机视觉的应用。这项工作由两卷组成,第一卷是线性代数,第二个是一种优化理论和应用,尤其是用于机器学习。这首卷涵盖了“经典”线性代数,直至主要构成和约旦形式。除了涵盖标准主题外,我们还讨论了一些对应用程序重要的主题。
数学(MATH1-UC)
Math1-UC 1180线性代数(4个学分)通常提供偶尔线性代数,与微积分一起,是计算和应用程序中最重要的数学领域之一。例如,它是数据挖掘的主要工具,即在大量数据集中识别模式的一组方法和过程。在许多应用中,该问题是数学提出的;然后将其转换为线性代数问题。线性代数问题得到解决,并解释了结果。在本课程中,学生学习了线性代数的理论概念和一些计算方法。分级:UC SPS分级可重复以获得额外信用:无先决条件:Math1-UC 1174。
生物学,技术和商业数学课程的模块手册
2个学士学位课程的数学模块5 2.1分析i。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。5 2.2分析II。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 6 2.3分析iii。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。5 2.2分析II。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。6 2.3分析iii。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。7 2.4分析IV。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 8 2.5线性代数i。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 9 2.6线性代数II。 。 。 。 。 。 。 。 。 。 。7 2.4分析IV。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。8 2.5线性代数i。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。9 2.6线性代数II。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。10 2.7句子性理论。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。11 2.8统计i。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。12 2.9统计II。 。 。 。 。 。12 2.9统计II。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。13 2.10线性优化和选定的主题。。。。。。。。。。。。。。。。。。。。。。。。14 2.11分析的数值方法。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。15 2.12线性代数的数值方法。。。。。。。。。。。。。。。。。。。。。。。。。。16 2.13实际研究阶段。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。17 2.14学士学位论文。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。18 2.15 Bachelorkolloquium。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。19
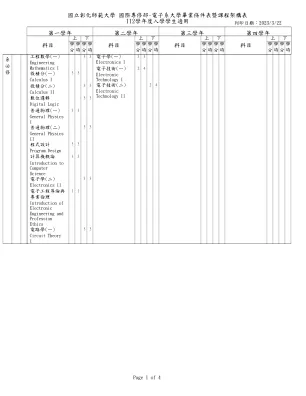
112学年度入学学生适用...
可穿戴系统设计组合语言33 3组装语言线性代数3 3线性代数讯号与系统3 3信号和系统资料结构33 3数据结构近代物理33 3 3 3 3 3 3 3 3 3
埃克塞特学院牛津夏季计划线性代数,优化和深度学习课程描述:本课程将
埃克塞特学院牛津夏季计划线性代数,优化和深度学习课程描述:本课程将通过三个相关任务探索现代数值算法:大规模线性代数,对数据科学的优化和深度学习。前六个讲座将讨论如何使用线性代数课程中未涵盖的技术近似求解大规模的线性代数任务。示例包括如何改善估计的解决方案,以及为何要为特征值解决比您可能相信的要容易得多。第二六个讲座将讨论优化算法,重点是大型数据科学任务。数值优化是最有用的技能之一,因为从科学到业务的许多任务都可以作为优化问题。六个研讨会将集中在深度学习上,这是推动机器学习和人工智能的最新进展的关键算法进步。深度学习用线性代数进行数学描述,学习是通过数值优化进行的,例如我们将要探索的学习。数字线性代数和优化的讲座将以知识良好的数值算法为基础,我们可以详细研究,而深度学习研讨会将使我们有机会探索促进AI革命的兴奋。教学大纲概述:讲座
光谱和代数图理论 - 计算机科学
对于那些需要线性代数介绍的人来说,与本书兼容的观点包含在吉尔·斯特朗(Gil Strang)的“线性代数介绍”中。有关线性代数的更高级主题,我建议罗杰·霍恩(Roger Horn)和查尔斯·约翰逊(Charles Johnson)的“矩阵分析”及其“矩阵分析中的主题”。对于与图形相关的物理系统的处理,我建议Gil Strang的“应用数学概论”,Sydney H. Gould的“特征值问题的变异方法”,以及Levin,Peres和Wilmer撰写的“特征值问题的变异方法”以及“ Markov Chains and Mighting Times”。
UMBC CMSC 491/691计算机视觉
我们将假设您在线性代数,几何,概率和Python编程中具有基本(但坚实的)基础。UMBC的推荐类是:数学221(线性代数),STAT 355或CMPE 320(概率和统计),数学151(微积分和分析几何学)。如果您与线性代数或微积分无关,则应考虑两者同时进行:如果没有这些工具,您可能会在课程上挣扎。尽管我们将简要介绍这些必要的主题,但CMSC 491/691不应是您对这些主题的首次介绍。我们了解,有些学生可能事先接触了信号/图像/音频处理,计算机图形,机器学习等。但是,这些都不是先决条件 - 该类被设计为独立的。
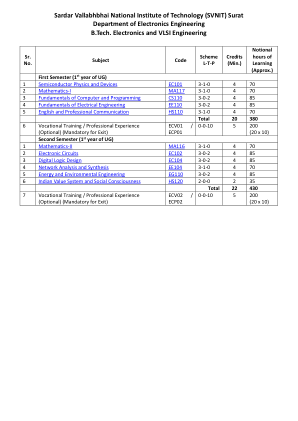
电子技术与超大规模集成电路工程学士
3. 教程 1 一阶常微分方程-I 2 一阶常微分方程-II 3 微分方程的应用 4 无限级数-I 5 无限级数-II 6 傅里叶级数-I 7 傅里叶级数-II 8 傅里叶积分与变换-I 9 傅里叶积分与变换-II 10 傅里叶积分与变换-II 11 贝塔函数与伽马函数-I 12 贝塔函数与伽马函数-II 13 线性代数方程组-I 14 线性代数方程组-II 15 线性代数方程组-III