XiaoMi-AI文件搜索系统
World File Search System量子态
通过改进的贪婪算法进行通用量子态准备
摘要：量子态的制备是量子信息处理的核心。贪婪算法提供了一种有效制备量子态的潜在方法。然而，标准贪婪算法通常不能取全局最大值，而是停留在局部最大值上。基于标准贪婪算法，本文提出了一种改进版本来设计动态脉冲以实现通用量子态制备，即从任意状态制备任意状态。作为应用，我们将该方案应用于半导体量子点和超导电路中单量子比特态和双量子比特态的通用制备。评估结果表明，我们的方案在具有同等高效率的同时，以更高的制备质量优于其他数值优化方法。与新兴的机器学习相比，它表现出更好的可访问性，并且不需要任何训练。此外，数值结果表明，我们的方案生成的脉冲序列对各种错误和噪声具有鲁棒性。我们的方案为少级系统和有限作用空间量子控制问题的优化开辟了一条新途径。
经典量子态条件熵的最佳均匀连续性界限
在这篇短文中，我将展示 Alhejji 和 Smith 最近的研究成果 [arXiv:1909.00787] 如何得出经典条件熵的最佳均匀连续性界限，从而得出经典量子态的量子条件熵的最佳均匀连续性界限。这个界限是最优的，因为总存在一对经典量子态达到界限的饱和，因此不可能再进一步改进。一个直接的应用是形成纠缠的均匀连续性界限，它改进了 Winter 先前在 [arXiv:1507.07775] 中给出的界限。关于条件熵的其他可能的均匀连续性界限，提出了两个有趣的未解决的问题，一个是关于量子经典态，另一个是关于完全量子二分态。
量子态转移：通过自旋链优化和构建的协议
大量研究已经概述了适当的光谱在通过自旋链镜像反转实现量子信息传输中的关键作用。通过结合数值和分析方法，研究人员已经确定了有利于完美或近乎完美状态转移（PST-PGST）的最近邻耦合和现场能量的配置。一个特别有效的模型，源自等距光谱（Christandl 等人），依赖于跨位点的强烈不均匀耦合，同时保持局部磁场不变。通过使用进化数值方法，特别是定制的遗传算法，我们发现了一种替代光谱。这种替代光谱仅通过调节现场能量即可实现高保真度的传输。这个光谱，最多大约一个位点，可以实现完全均匀的耦合，从而简化了实验要求。我们还使用了逆特征值方法中的辅助数值方法来提供辅助分析，以区分准完美状态转移 (QPST) 和 PST，并强调两者之间的权衡。通过这些分析，我们可以提出替代方案，为实验实施提供潜在优势，同时仍以完美或近乎完美的状态转移为目标。
时空高效的低深度量子态制备及其应用
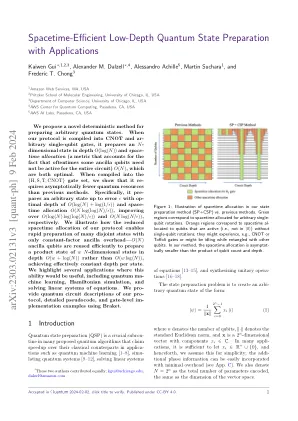
我们提出了一种用于准备任意量子态的新型确定性方法。当我们的协议被编译成 CNOT 和任意单量子比特门时，它会准备一个深度为 O (log( N )) 的 N 维状态，时空分配（一种度量标准，它考虑到某些辅助量子比特通常不需要在整个电路中处于活动状态）为 O ( N ) ，这两者都是最优的。当编译成 { H , S , T , CNOT } 门集时，我们表明它比以前的方法需要更少的量子资源。具体来说，它可以准备一个任意状态，误差不超过 ϵ，最佳深度为 O (log( N ) + log(1 /ϵ ))，时空分配为 O ( N log(log( N ) /ϵ ))，分别优于 O (log( N ) log(log( N ) /ϵ )) 和 O ( N log( N/ϵ ))。我们说明了我们的协议如何通过减少时空分配来快速准备许多不相交状态，而只需要常数因子辅助开销——O ( N ) 个辅助量子位被有效地重用，以准备深度为 O (w + log( N )) 而不是 O (w log( N )) 的 w N 维状态的乘积状态，从而有效地实现每个状态的恒定深度。我们重点介绍了这种能力有用的几个应用，包括量子机器学习、汉密尔顿模拟和求解线性方程组。我们提供我们的协议的量子电路描述、详细的伪代码和使用 Braket 的门级实现示例。
量子态和 SPAM 噪声同时断层扫描的通用框架
洛斯阿拉莫斯国家实验室是一家采取平权行动/提供平等机会的雇主，由 Triad National Security, LLC 为美国能源部国家核安全局运营，合同编号为 89233218CNA000001。通过批准本文，出版商承认美国政府保留非独占的、免版税的许可，可以为了美国政府的目的出版或复制本文的已发表形式，或允许他人这样做。洛斯阿拉莫斯国家实验室要求出版商将本文注明为在美国能源部的支持下完成的工作。洛斯阿拉莫斯国家实验室坚决支持学术自由和研究人员的发表权利；但是，作为一个机构，实验室并不认可出版物的观点，也不保证其技术上的正确性。
射影环面设计、差集和量子态设计
𝑡 次三角立方规则是环面上的点集，在这些点集上，总和可重现整个环面上 𝑡 次单项式的积分。它们可以被认为是环面上的 𝑡 -设计。受量子力学的射影结构的启发，我们发展了射影环面上的 𝑡 -设计的概念，令人惊讶的是，它们的结构比整个环面上的对应设计要严格得多。我们提供了这些射影环面设计的各种构造，并证明了它们的大小和结构特征的一些界限。我们将射影环面设计与一系列不同的数学对象联系起来，包括来自加法组合学领域的差集和 Sidon 集、来自量子信息论的对称、信息完备的正算子值测度 (SIC-POVM) 和相互无偏基 (MUB) 的完备集（据推测与有限射影几何有关）以及某些根格的水晶球序列。利用这些联系，我们证明了密集 𝐵 𝑡 mod 𝑚 集的最大大小的界限。我们还使用射影环面设计来构建量子态设计系列。最后，我们讨论了许多关于这些射影环面设计的性质的未解决的问题，以及它们与数论、几何和量子信息中的其他问题的关系。
非线性超表面对量子态的全光调制
摘要 超表面已证明具有在纳米尺度上利用光的奇异能力，这不仅对经典光学而且对量子光学都很重要。量子态的动态操控是量子信息处理的核心；然而，到目前为止，这种功能很少在超表面中实现。本文，我们报告了一种利用非线性超表面对光子量子态进行全光动态调制的方法。该超表面由金属纳米结构和光异构化偶氮层组成。通过光学切换偶氮分子在二元异构态之间来调节等离子体共振，我们实现了对正交偏振光子传输效率以及它们之间的相位延迟的动态控制，从而有效控制纠缠态。作为一个例子，量子态蒸馏已被证明可以将贝尔态从非最大纠缠态恢复到保真度高于 98% 的贝尔态。我们的工作将丰富超表面在量子世界中的功能，从静态到动态调制，使量子超表面走向实用。
新兴量子态设计和对偶中的双元性
最近的研究调查了量子猝灭后幺正动力学中一种新型随机矩阵行为的出现。从时间演化状态开始，通过对系统剩余部分进行投影测量，可以生成一个由小子系统支撑的纯态集合，从而得到一个投影集合。在混沌量子系统中，人们推测这种投影集合与均匀的 Haar 随机集合变得难以区分，并导致量子态设计。Ho 和 Choi 最近 [ Phys. Rev. Lett. 128, 060601 (2022) ] 给出了在自对偶点处踢动 Ising 模型的精确结果。我们提供了一种可扩展到具有可解初始状态和测量值的一般混沌对偶单元电路的替代构造，突出了底层对偶单元性的作用，并进一步展示了对偶单元电路模型如何同时表现出精确的可解性和随机矩阵行为。基于双单元连接的结果，我们展示了复杂的 Hadamard 矩阵和单元误差基如何都导致可解的测量方案。
来自量子混沌动力学的精确涌现量子态设计
我们给出了一种新型的随机矩阵普适性的精确结果，这种普适性是无限温度下量子多体系统可以表现出的。具体来说，我们考虑一个纯态集合，该集合由一个小的子系统支撑，该子系统是通过对系统其余部分进行局部投影测量而生成的。我们严格地证明了，从一类经历淬火动力学的量子混沌系统推导出的集合接近于一种完全独立于系统细节的普适形式：它在希尔伯特空间中均匀分布。这超越了量子热化的标准范式，该范式规定子系统放松为一个量子态集合，该集合再现了热混合状态下局部可观测量的期望值。我们的结果更普遍地意味着量子态本身的分布与均匀随机态的分布变得难以区分，即集合形成了量子信息论术语中的量子态设计。我们的工作建立了量子多体物理学、量子信息和随机矩阵理论之间的桥梁，表明伪随机态可以从孤立的量子动力学中产生，为设计量子态断层扫描和基准测试的应用开辟了新方法。