XiaoMi-AI文件搜索系统
World File Search System量子算法和遗忘的力量 - DROPS
所谓的焊接树问题是黑箱问题的一个例子,量子行走可以比任何经典算法 [3] 更快地解决该问题。给定一个特殊入口顶点的名称,量子行走可以使用多项式次数的查询找到另一个独特的出口顶点,尽管找不到从入口到出口的任何特定路径。二十年来,是否存在有效的量子算法来寻找这样的路径,或者路径寻找问题即使对于量子计算机来说是否也很难,这一直是一个悬而未决的问题。我们表明,一类自然的高效量子算法可以证明无法找到从入口到出口的路径。具体而言,我们考虑在算法叠加的每个分支中始终存储一组顶点标签,这些标签形成包含入口的连通子图,并且仅将这些顶点标签作为 oracle 的输入。虽然这并不排除量子算法能够有效找到路径的可能性,但尚不清楚算法如何通过偏离这种行为而受益。我们的无效结果表明,对于某些问题,量子算法必须忘记它们采取的解决问题的路径,才能胜过经典计算。
使用图理论的概念
摘要 - 现代世界使每个人都通过数字通信更加接近。人们高度依赖数字服务。寻求更复杂的编码算法,以防止数据违反,这是永无止境的。算法越复杂,通信将更安全。因此,Vogue是要找到最令人费解的算法来提供安全的通信。在本文中,使用图形标签(图形和广义补充的补充)开发了一种唯一的算法。该算法生成了两个标记的图形,这些图形满足顶点均值和顶点奇数均值标记。加密涉及通过图的k汇编以获得密码图的互补过程和组合两个图。将反向过程应用于解密,涉及将密码图分为两个子图,通过将k-complement应用于顶点集的指定分区,以使用图形标记方法获取获得的图形/s的补充,并获取明文的补充。所提出的算法的设计方式,即使具有特殊字符,也应对各种明文有用。为了说明这一点,在Android平台中开发了一个应用程序,用于使用End-End加密来通信消息。
Hedin方程 div>
hedin的方程式提供了一条优雅的途径,可以通过一组非线性方程的自洽迭代来计算确切的一体绿色功能(或传播器)。其一阶近似(称为GW)对应于环图的重新介绍,并且在物理和化学方面已显示出非常成功的。通过引入顶点校正,尽管具有挑战性,可以进行系统的改进。 考虑到异常的传播器和外部配对电位,我们得出了一组与著名的Hedin方程相等的封闭方程组,但作为第一阶近似值,粒子粒子(PP)t -matrix近似值,在此执行梯形图的分解。 通过考虑低阶PP顶点校正,HedIn方程的PP版本提供了一种系统地超越T -Matrix近似的方法。可以进行系统的改进。考虑到异常的传播器和外部配对电位,我们得出了一组与著名的Hedin方程相等的封闭方程组,但作为第一阶近似值,粒子粒子(PP)t -matrix近似值,在此执行梯形图的分解。通过考虑低阶PP顶点校正,HedIn方程的PP版本提供了一种系统地超越T -Matrix近似的方法。
JP 1-01.1,联合出版物汇编
• 联合出版物层次结构 ................................................................................................ v • 联合出版物标识 ...................................................................................................... v • 联合条令开发 ...................................................................................................... v • 顶点条令出版物 ...................................................................................................... vii • 支持出版物 ...................................................................................................... viii
关于量子退火器的高质量嵌入的讨论
人们已经尝试过多种方法来设计有效的方法来寻找 QA 中 Ising 问题的映射。这些尝试可以分为两类。第一种方法是寻找具有近乎最优嵌入的完全图的嵌入,同时考虑目标图的结构。第一项工作是由 V. Choi [3] 提出的,它提供了三角布局上完全图的最佳嵌入(TRIAD 方案)。这项初步工作由 C. Klymko 等人完成。[6],他们提出了一种次要嵌入方法,专门用于在由定期分派的完全连通二分子图组成的格子上查找团嵌入。该方法考虑不可操作的量子位(目标图通常包含一些禁用的量子位),并生成从初始近乎最优的团嵌入派生的有效嵌入。第二种方法考虑在部分已知或未知的目标图上嵌入未知结构化输入图的算法。[2] 中提出了一种初始的通用启发式方法,并在 [4] 中实现。该算法由两步组成:第一步是为每个逻辑量子位找到一个允许重叠的初始映射(即,顶点 v ∈ V t 可能映射 V s 中的多个顶点 ϕ ( v )。第二步是细化,通过删除顶点映射 ϕ ( v ) 并寻找该顶点的更好映射来迭代改进映射,从而最小化物理顶点的总数。顶点映射的质量用成本函数计算。没有任何重叠的输出图被认为是有效的。当在特定次数的尝试期间没有取得任何改进时,细化阶段结束。其他几种启发式算法一直在重复使用这种算法
职业治疗博士课程...
摘要:这个顶点项目是倡导和教育的渠道,旨在解决寄养儿童的社会不公问题,使他们能够提高日常生活中的整体职业表现。在这个顶点项目中,创建了一个资源笔记本,其中包含活动想法,包括活动分析,以及供治疗师和寄养儿童现在和以后参考的教育讲义。这个顶点项目是阿肯色州莫里尔顿治疗诊所生活技能和过渡实验室的启动项目。向南方基督教儿童之家和治疗猴子推荐并提交了短期和长期设计计划,以便未来做出开发生活技能和过渡实验室物理空间的决定。在资源笔记本中,重点主要解决 IADL,例如:杂货、烹饪和烘焙、资金管理、家庭管理和洗衣护理以及社交技能和沟通。涉及的过渡服务包括职业探索、职业准备、求职和就业。在生活技能和过渡实验室的物理空间内进行的改变包括清洗混凝土地板和楼梯、打磨和粉刷楼梯以及移除多余的家具。南方基督教儿童之家和 Therapy Monkey 已向其推荐并提供了物理空间的下一步措施。
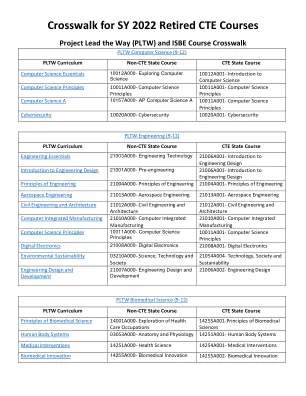
2022 学年已停用的 CTE 课程
21054A001- 技术设计与创新 先进设计应用 21006A000- 工程设计 21006A002- 工程设计 先进技术应用 21006A000- 工程设计 21006A002- 工程设计 工程设计(顶点) 21006A000- 工程设计 21006A002- 工程设计