XiaoMi-AI文件搜索系统
World File Search SystemKaratsuba算法:使用CUDA
摘要 - 在任意算术计算和计算科学中,大型整数乘以广泛使用的操作。许多加密技术涉及对整数的极大子集进行操作,包括Diffie-Hellman密钥交换,RSA,ECC等。这些技术采用安全消息加密,解密和密钥交换,使用其大小至少1024位的安全键。的指控和乘法。Karatsuba算法是一种快速有效的方法,用于繁殖大数量,在每个递归步骤中,将乘法数量从四个减少到三个。在本文中,当应用于顺序和平行环境时,我们对卡拉茨巴算法的性能进行了全面评估。我们使用计算统一设备体系结构(CUDA)编程的NVIDIA图形处理单元(GPU)的功能来衡量并行实现和处理器配置的加速。在连续的NVIDIA GPU CUDA平台上运行的Karatsuba算法达到的加速度为30.12。通过利用可用的GPU内核可以改善性能。这些发现强调了平行化在减少总体计算时间方面的潜在优势。索引术语 - Karatsuba,乘法,计算统一设备体系结构,NVIDIA图形处理单元,加速
高性能M- Term Karatsuba类似于...
I.简介技术在日常工作和企业中都具有重要作用。它以各种方式使用,并提供各种目的。人工智能最近越来越受欢迎。人工智能(AI)模拟了人类的认知功能。更具体地说,与人类非常接近,AI聊天机器人目前正在此软件中代替人类响应。聊天机器人是一款计算机程序,充当虚拟助手和人类与机器人之间的桥梁。近年来,它的突出是由于技术的巨大进步。人工智能,机器学习和其他基本主题,例如自然语言处理和神经网络。这些聊天机器人表现出色。要与任何个人进行对话,请使用交互式查询。最近可用于改进和扩展聊天机器人行业的基于云的聊天机器人服务的数量已激增。IBM Watson,Cleverbot,Eliza Chatbot和无数其他服务就是这些服务的示例。近年来,人类机器人对话的艺术已经显着发展,这些对话代理人变得更加容易受到接受。
13 I 2025年1月https://doi.org/10.22214/ ...
工程学院,奎师那dt。,安得拉邦摘要:有限的场乘法在加密电路中起着至关重要的作用,因为其广泛应用。但是,由于其复杂性,这些乘法的建筑电路构成了重大挑战。为了减轻这种情况,使用Karatsuba算法,将每个数字分为N/2位以降低空间复杂性。这种方法降低了空间的复杂性,但也会增加时间复杂性。在我们的研究中,我们引入了一种混合方法,实施了类似Karatsuba的乘数,该乘数结合了Karatsuba和SBM(学校图书乘法)技术的元素。在拟议的设计中,我们用华莱士树乘法器替换阵列乘数,以进一步提高设计性能。这种组合有效地降低了时间和空间的复杂性。根据报告的设备利用和潜伏期,我们的发现表明,所提出的乘数在速度和效率方面比标准的Karatsuba乘数优于标准的Karatsuba乘法器,尤其是在该地区 - 德莱产品指标。关键字:二进制多项式乘数,现场可编程的门阵列(FPGA),有限的场乘法,华莱士树乘数,M-Term Karatsuba类似。
用于二进制场乘法的 Toffoli 门数优化的空间高效量子电路
摘要:Shor 算法在多项式时间内解决了椭圆曲线离散对数问题 (ECDLP)。为了优化二进制椭圆曲线的 Shor 算法,降低二进制域乘法的成本至关重要,因为它是最昂贵的基本算法。在本文中,我们提出了用于二进制域 (F 2 n) 乘法的 Toffoli 门数优化的空间高效量子电路。为此,我们利用类 Karatsuba 公式并证明其应用可以在没有辅助量子位的情况下提供,并在 CNOT 门和深度方面对其进行了优化。基于类 Karatsuba 公式,我们驱动了一种空间高效的基于 CRT 的乘法,该乘法采用两种非原地乘法算法来降低 CNOT 门成本。我们的量子电路不使用辅助量子位,并且 TOF 门数极低,为 O ( n 2 log ∗ 2 n ),其中 log ∗ 2 是一个增长非常缓慢的迭代对数函数。与最近基于 Karatsuba 的空间高效量子电路相比,我们的电路仅需要 Toffoli 门数的 (12 ∼ 24%),且加密字段大小 ( n = 233 ∼ 571 ) 具有可比深度。据我们所知,这是第一个在量子电路中使用类似 Karatsuba 的公式和基于 CRT 的乘法的结果。
二进制椭圆曲线的另一个具体量子隐式分析
摘要。本文为二进制椭圆曲线提供了具体的量子密码分析,以实现时间效率的实现透视(即减少电路深度),并补充Banegas等人的先前研究,该研究的重点是空间效率的效率(即电路宽度)。为了实现深度优化,我们提出了改进Karatsuba乘数和基于FLT的反转的现有电路实现,然后在Qiskit Quantum Computer Simulator中构建和分析资源。提出的乘数架构,改善了Van Hoof等人的量子Karatsuba乘数,减少了与O(n log 2(3))界限的深度和较低的CNOT门,同时保持了相似数量的to效应和鸡蛋。此外,我们所证明的基于FLT的反演会减少CNOT数量和整体深度,并具有较高的量子量。最后,我们采用了拟议的乘数和基于FLT的IN-版本来执行二进制点添加的量子隐性分析以及用于椭圆曲线离散对数问题(ECDLP)的完整shor的算法。结果,除了减小深度外,与先前的工作相比,我们还能够降低多达90%的to oli门,从而显着改善,并提供对量子密码分析的新见解,以实现高度优化的实施。
探索针对内存计算的密码学的大整数乘法
摘要 - 出现的加密系统,例如完全型号的加密(FHE)和零知识证明(ZKP)是计算和数据密集型的。fhe和ZKP在软件和硬件中的影响很大程度上依赖于von Neumann架构,在数据移动上损失了大量的能量。有希望的计算范式正在内存(CIM)中进行计算,该计算使计算能够直接发生在内存中,从而减少数据运动和能耗。但是,有效地执行大整数乘法(在FHE和ZKP中至关重要)是一个开放的问题,因为现有的CIM方法仅限于小型操作数尺寸。在这项工作中,我们通过探索用于大整数乘法的高级算法方法来解决这个问题,并将Karatsuba算法确定为CIM应用程序最有效的方法。此后,我们设计了第一个用于电阻CIM横杆的Karatsuba乘数。我们的乘数使用三阶段管道来增强吞吐量,此外,还可以平衡内存耐力与有效的数组大小。与现有的CIM乘法方法相比,当比例扩展到ZKP和FHE所需的位宽度时,我们的设计在吞吐量中最多可实现916倍,而面积时间产品的改进则达到281倍。索引术语 - 在内存中计算,大整数乘以,karatuba乘法
课程简介
一些加密货币基于“不错的”假设。例如,Rabin密码系统基于保理的硬度。 这是一种“双赢”情况:我们有一个安全的加密系统,或者我们得到了一种保理算法(这将是令人兴奋的)。 我们可以将块密码基于“良好”的假设,例如假设很难,但是由此产生的密码系统太慢。 例如,基于大数字的分解和基于离散的操作的代价高昂,主要是因为此大小数量的最快的乘法算法在数字中的位数中是超线性的。 学科乘法算法算法乘以时间o(n 2)。 对于RSA大小的数字,您可能会在时间O(n 1.58)中使用高级karatsuba方法,但我们通常不会超越这一点。例如,Rabin密码系统基于保理的硬度。这是一种“双赢”情况:我们有一个安全的加密系统,或者我们得到了一种保理算法(这将是令人兴奋的)。我们可以将块密码基于“良好”的假设,例如假设很难,但是由此产生的密码系统太慢。例如,基于大数字的分解和基于离散的操作的代价高昂,主要是因为此大小数量的最快的乘法算法在数字中的位数中是超线性的。学科乘法算法算法乘以时间o(n 2)。对于RSA大小的数字,您可能会在时间O(n 1.58)中使用高级karatsuba方法,但我们通常不会超越这一点。
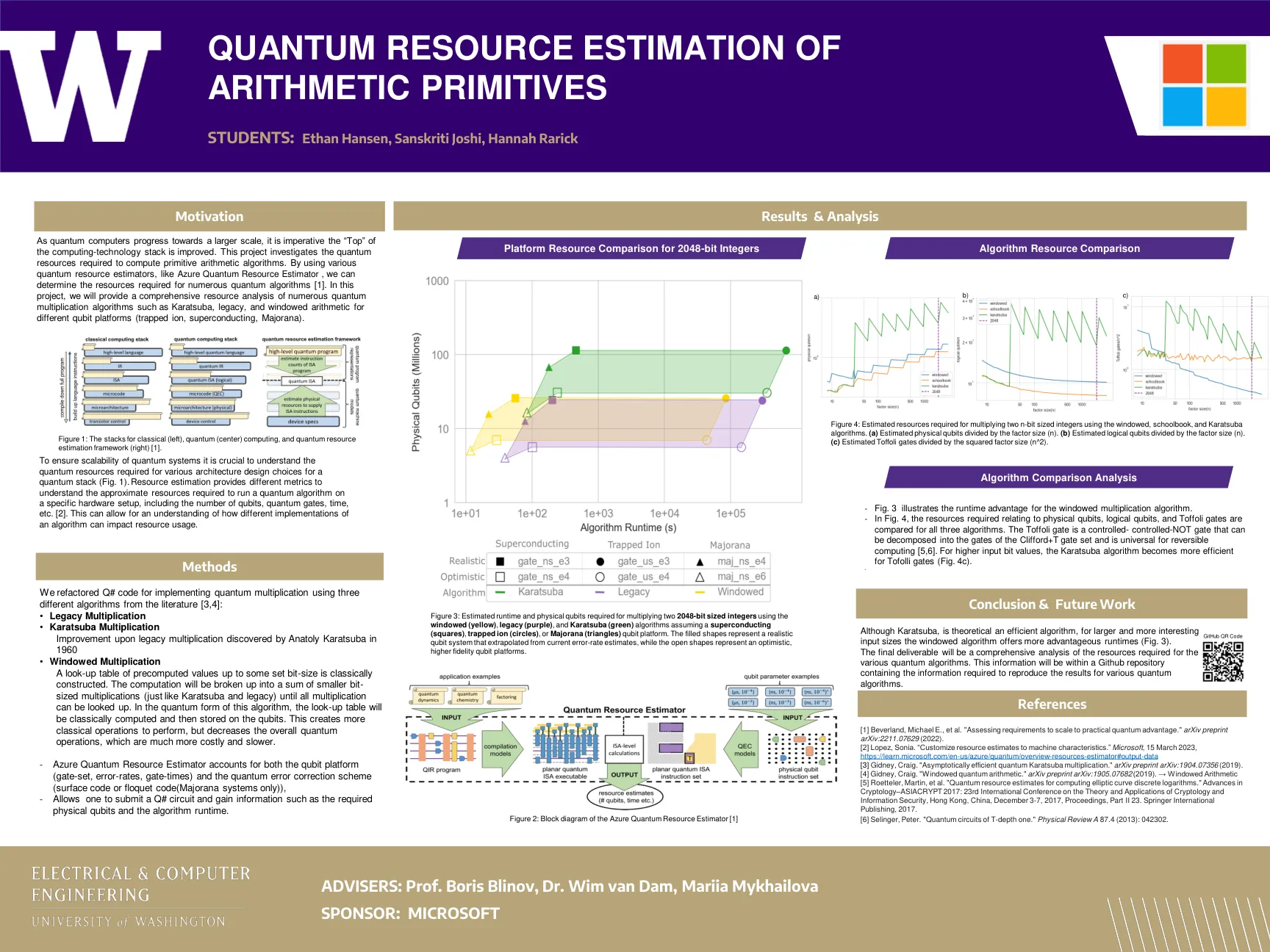
算术原语的量子资源估计
[1] Beverland, Michael E. 等人。“评估需求以扩展到实际的量子优势。” arXiv 预印本 arXiv:2211.07629 (2022)。[2] Lopez, Sonia。“根据机器特性定制资源估算。” Microsoft ,2023 年 3 月 15 日,https://learn.microsoft.com/en-us/azure/quantum/overview-resources-estimator#output-data [3] Gidney, Craig。“渐近有效的量子 Karatsuba 乘法。” arXiv 预印本 arXiv:1904.07356 (2019)。[4] Gidney, Craig。“窗口量子算术。” arXiv 预印本 arXiv:1905.07682 (2019)。→ 窗口算术 [5] Roetteler, Martin 等人。 “计算椭圆曲线离散对数的量子资源估计。”《密码学进展 - ASIACRYPT 2017:第 23 届密码学和信息安全理论与应用国际会议》,中国香港,2017 年 12 月 3 日至 7 日,会议录,第 II 部分 23。Springer International Publishing,2017 年。[6] Selinger,Peter。“T 深度一的量子电路。”《物理评论 A》87.4(2013):042302。
使用 AlphaTensor 进行量子电路优化
实现容错量子计算机的一个关键挑战是电路优化。我们专注于容错量子计算中最昂贵的门(即 T 门),解决 T 计数优化问题,即最小化实现给定电路所需的 T 门数量。为了实现这一目标,我们开发了 AlphaTensor-Quantum,这是一种基于深度强化学习的方法,利用优化 T 计数和张量分解之间的关系。与现有的 T 计数优化方法不同,AlphaTensor-Quantum 可以结合有关量子计算的领域特定知识并利用小工具,从而显著减少优化电路的 T 计数。AlphaTensor-Quantum 在一系列算术基准上的表现优于现有的 T 计数优化方法(即使在不使用小工具的情况下进行比较)。值得注意的是,它发现了一种类似于 Karatsuba 有限域乘法方法的有效算法。 AlphaTensor-Quantum 还为 Shor 算法中使用的相关算术计算和量子化学模拟找到了最佳的人为设计解决方案,从而证明它可以通过完全自动化的方式优化相关量子电路来节省数百小时的研究时间。
Toom三路乘法的量子电路设计
摘要:在经典计算中,Toom-Cook 是一种大数乘法方法,与其他算法(如教科书乘法和 Karatsuba 乘法)相比,其执行时间更快。对于量子计算中的使用,先前的工作考虑了 Toom-2.5 变体,而不是经典的更快、更突出的 Toom-3,主要是为了避免后者电路固有的非平凡除法运算。在本文中,我们研究了 Toom-3 乘法的量子电路,预计该电路的深度会比 Toom-2.5 电路的渐近更低。具体来说,我们设计了相应的量子电路,并采用了 Bodrato 提出的序列,以减少运算次数,特别是在非平凡除法方面,每次迭代减少到仅一次精确的 3 除法电路。此外,为了进一步降低剩余除法的成本,我们利用特定除法电路的独特属性,将其替换为常数乘以互易电路和相应的交换运算。我们的数值分析表明,与 Toom-2.5 相比,所得电路在 Toffoli 深度和量子比特数方面确实具有较低的渐近复杂度,但具有大量主要来自于实现除法运算的 Toffoli 门。