XiaoMi-AI文件搜索系统
World File Search System基于SVM的EEG信号分类,改进...
摘要:脑电图(EEG)是一个复杂的生物选择信号。分析可以为搜索者提供有用的生理信息。为了识别和分类EEG信号,提出了一种使用改进的松鼠搜索算法(ISSA)来优化支持向量机(SVM)的模式识别方法。预处理EEG信号,其时域特征将被提取并针对SVM作为分类和识别的特征向量。在本文中,良好点集的方法用于初始化人口位置,混乱和反向学习机制被引入算法中。使用基准功能进行了改进的松鼠算法(ISSA)的性能测试。从结果的统计分析可以看出,算法的勘探能力和收敛速度可以提高。然后将其用于优化SVM参数。ISSA-SVM模型是为EEG信号的分类而建立的。对于数据集,该方法的平均分类为85.9%。此结果比比较方法提高了2-5%。
慢性神经性疼痛中的EEG频带分析
背景和目标:慢性神经性疼痛(NP)是一种慢性疼痛疾病,严重影响患者的生活。疼痛管理被证明是不可能的。提供NP相关信息的低成本,无创工具是脑电图(EEG)。但是,事实证明,常用的线性脑电图特征在表征NP病理生理学方面受到限制。本研究试图确定非线性脑电图特征(例如近似熵(APEN))是否比绝对条带功率更好地区分疼痛严重性。方法:基于简短疼痛清单(BPI)的非参数统计方法,以及线性和非线性EEG特征。为此,招募了36例慢性NP患者,并注册了22个渠道。此外,将13名参与者的控制数据库用作参考,其中有19个通道注册。对于两组,在静止状态下记录了脑电图10分钟:5分钟,眼睛睁开(EO)和5分钟,闭上眼睛(EC)。在两组的所有通道中估计了五个临床频带(Delta,Theta,Alpha,beta和Gamma)中五个临床频带(Delta,Theta,Alpha,Beta和Gamma)中的绝对带功率和APEN EEG特征。结果,分别为实验和对照类别获得了220维和190维特征向量。对于实验类别,NP患者根据BPI评估分为三组:低,中度和高疼痛。©2023作者。由Elsevier B.V.最后,使用Kruskal Wallis和Hoc Dunn的测试比较组之间的特征向量。结果:APEN揭示了大多数频段和组之间的统计差异(P <= 0.0 0 01)。相比之下,群体之间的差异较小,尤其是在EO之间。此外,NP组仅在Theta,Alpha和Beta带中仅使用APEN聚集。结论:结果表明,APEN有效地表征了慢性NP的不同严重性,而不是常用的线性特征。APEN和其他非线性技术(例如,光谱熵,香农熵)可能是监测慢性NP体验的更合适的方法。这是CC下的开放式访问文章(http://creativecommons.org/licenses/4.0/)
人工智能算法预测骨科手术后处方镇痛鸡尾酒的疗效
骨科手术后使用止痛药缓解术后疼痛是围手术期医学的一个主要问题。特别是在肩部手术(例如肩袖修复)、全关节置换和肢体创伤的情况下,预计疼痛程度会很高;因此,必须采用高效的策略来加快恢复,避免患者不适和痛苦,并降低疼痛相关并发症的风险 [ 1 – 3 ]。在多模式疼痛治疗中,医生通常会联合使用两种或两种以上的止痛药 [ 4 , 5 ]。由于这些药物之间可能存在药理学相互作用,因此很少知道疗效的预测。相互作用可以基于作用机制(例如受体上的药效学)或药代动力学途径。例如,高达 95% 的双氯芬酸在吸收后与血清白蛋白结合,在肝脏中经 CYP 3A4 羟基化和葡萄糖醛酸化后经肾脏消除。临床效果是通过阻断环氧合酶 I 和 II 实现的,从而导致前列腺素的合成减少。对乙酰氨基酚也通过环氧合酶途径表现出其作用,抑制前列腺素合成。另一方面,阿片类药物通过受体起作用,这些受体对这些镇痛药具有特异性,在肝脏中经 CYP 3A4 羟基化后消除。因此,对于临床医生来说,两种以上药物的组合可能不清楚,并且对处方的净效应感到困惑。术后处方中含有具有各种药代动力学和药效学特性的阿片类药物和非阿片类药物。据我们所知,关于当以两种以上药物组合使用时这些特性如何变化的数据很少,而且很少发表(如果有的话)[6-11]。对具有大量止痛药组合的止痛药的任何统计评估都面临着严峻的挑战:使用传统统计方法得出结论极其困难。我们使用人工智能方法 [12-15] 来克服这一困难。我们使用(人工)神经网络(NN)进行数据分析;具体来说,我们使用称为自动编码器的无监督神经网络(图 1)。这些无监督神经网络通过最小化损失(输入和输出之间的差异的平方和,在训练集上取平均值)来生成高精度模拟输入的输出(因此得名:自动编码器)。特征向量在下一段中描述。然后,我们将每个输入特征向量的代码层权重用作降维特征向量的坐标(图 1)。疼痛程度是分类变量,所施用的止痛药也是如此。我们使用独热编码为每个患者生成一个 38 维特征向量(参见方法部分)。这些特征向量并不独立。降维算法(神经网络自动编码器)找到独立性并将结果映射到二维流形(平面图)上。每个患者都是这个平面上的一个点,这些点不是随机分布的;相反,它们是聚集的。在我们掌握的众多聚类算法中,我们使用 DBSCAN 聚类算法 [ 16 ],因为将其应用于点可以识别出具有许多共同止痛药的鸡尾酒聚类。相互依赖性产生包含高效止痛药的聚类;正如我们下面讨论的那样,这一发现无法通过任何其他方式找到(有 61 种不同的止痛药鸡尾酒,总共 750×2 = 1500 种疼痛
利用心电图信号进行深度学习驱动的心脏病预测
ECG 结构的非平稳动机是评估心跳速度和节律的重要读数,因此可以评估心脏的健康状况。本文提出了一种用于自动 ECG 分类的稳健方法,将数据分为两类:正常和病理性心血管模式的变化。更具体地说,收集到的 ECG 信号被归一化、过滤以消除噪声干扰。因此,形态属性被形成以尽可能地表示类别的特征。ACO 被纳入分割和特征选择中,以减少异常的特征向量。ECG 信号的分类是通过使用双长期短期记忆 (Bi-LSTM) 神经网络进行的,因为它是一种经过验证的序列预测网络,并且能够捕获数据中的长期时间依赖性。评估标准表明,相对于其他提出的 ECG 分类,所提出的方法达到了 90% 的分类准确率。已经确定 ACO 与 Bi-LSTM 的结合提供了改进的 ECG 分类,从而使其成为临床诊断和治疗监测的有用工具。
基于一致性评价的药物-靶标亲和力预测方法...
摘要 - 药物发现的第一步是找到具有针对特定靶标的药用活性的药物分子部分。因此,研究药物靶标蛋白与小化学分子之间的相互作用至关重要。然而,传统的发现潜在小药物分子的实验方法劳动密集且耗时。目前,人们对使用药物分子相关数据库建立计算模型来筛选小药物分子非常感兴趣。在本文中,我们提出了一种使用深度学习模型预测药物靶标结合亲和力的方法。该方法使用改进的GRU和GNN分别从药物靶标蛋白序列和药物分子图中提取特征以获得它们的特征向量。组合向量用作药物-靶标分子对的向量表示,然后输入到完全连接的网络中以预测药物-靶标结合亲和力。该提出的模型证明了其在DAVIS和KIBA数据集上预测药物-靶标结合亲和力的准确性和有效性。
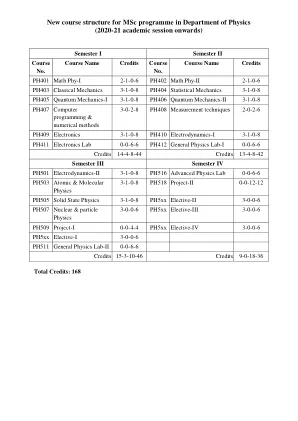
物理系理学硕士课程的新课程结构
PH401:数学物理 I (2-1-0-6) 线性代数:线性向量空间:对偶空间和向量、柯西-施瓦茨不等式、实数和复数向量空间的定义、度量空间、线性算子、子空间;跨度和线性独立性:行减少和方法;基础和维度:使用简化的跨度和独立性测试 (RREF) 方法;线性变换:图像、核、秩、基础变换、转移矩阵、同构、相似变换、正交性、Gram-Schmidt 程序、特征值和特征向量、希尔伯特空间]。张量:内积和外积、收缩、对称和反对称张量、度量张量、协变和逆变导数。常微分方程和偏微分方程:幂级数解、Frobenius 方法、Sturm-Liouville 理论和边界值问题、格林函数;笛卡尔和曲线坐标系中不同波动方程的分离变量法,涉及勒让德、埃尔米特、拉盖尔和贝塞尔函数等特殊函数以及涉及格林函数的方法及其应用。教材:
关岛两个主要礁石中的珊瑚移植分析
抽象的珊瑚礁是至关重要的海洋生态系统,面临着气候变化和人类活动的前所未有的威胁。珊瑚移植是一种常用的恢复技术,但是在这些移植的珊瑚中,很少有关于微生物动力学的研究。本研究旨在阐明关岛皮蒂礁中与移植珊瑚有关的细菌网络。数据侧重于主要的礁石分类单元,porites cylindrica和porites lobata。根据时间和位置比较珊瑚中存在的细菌家族。这项研究利用中心性来了解细菌网络的结构和动力学,揭示了促进微生物群落之间相互作用的细菌家族。特征向量的中心性揭示了网络稳定性的贡献者以及健康和疾病的可能指标的影响。高照明进一步分析和与数学分析的联系,结果表明,在转移期内,细菌具有较高的中间和特征向量中心。
使用支持向量机进行飞机飞行控制执行器故障检测
摘要:未来几代飞行控制系统,例如无人驾驶飞行器 (UAV) 的飞行控制系统,可能会更具适应性和智能性,以应对无人驾驶带来的额外安全性和可靠性要求。高效的故障检测和隔离 (FDI) 系统至关重要,应该能够监控飞机的健康状况。从历史上看,硬件冗余技术已用于检测故障。然而,由于成本高且附加组件质量大,在无人机中复制执行器并不理想。幸运的是,也可以使用分析冗余技术检测飞机执行器故障。在本研究中,设计了一种使用支持向量机 (SVM) 的数据驱动算法。所研究的飞机执行器故障是效率损失 (LOE) 故障。故障检测算法的目的是根据执行器的健康状况将特征向量数据分类为正常或故障类。结果表明,SVM 算法几乎可以立即检测到 LOE 故障,平均准确率为 99%。
有向图上的谐波分析及应用
我们针对定义在强连通有向图(有向图)顶点上的函数引入了一种新颖的谐波分析,其中随机游走算子是其基石。首先,我们将随机游走算子的特征向量集视为有向图上函数的非正交傅里叶型基。我们通过将从其狄利克雷能量获得的随机游走算子的特征向量变化与其相关特征值的实部联系起来,找到了一种频率解释。从这个傅里叶基开始,我们可以进一步进行并建立有向图的多尺度分析。我们提出了一种冗余小波变换和抽取小波变换,分别作为有向图的谱图小波和扩散小波框架的扩展。因此,我们对有向图的谐波分析的发展使我们考虑应用于有向图的半监督学习问题和图上的信号建模问题,突出了我们框架的效率。
博士课程的教学大纲
1。数学物理学(信用:3,约25小时)Phys04-001-C线性向量空间,线性操作员和矩阵,线性方程系统。特征值和特征向量。张量:引言和定义,对称和反对称张量,笛卡尔和非笛卡尔张量和协变量导数,基督教符号,不可减至表示,直接产物和收缩,牛顿力学和相对论中的张量。线性普通微分方程,物理学中的线性偏微分方程,绿色功能,变量解决方案方法的分离,特殊功能及其在物理学中的应用。复杂的变量理论;分析功能。Taylor和Laurent扩展,分析延续,轮廓整合,分散关系。积分方程:Fredholm和Volterra方程,微分方程向积分方程的转换,求解积分方程的方法。有限和连续群体简介。小组表示和操作,置换组及其表示群体。建议的书: