XiaoMi-AI文件搜索系统
World File Search System跨受试者脑电情绪分类的迁移判别词典对学习方法
脑电信号具有不易伪装、可携带、无侵入等特点,在情绪识别中被广泛应用。然而由于个体差异的存在,不同受试者的同一种情绪状态下的脑电信号数据分布会存在一定的差异。传统的情绪识别方法为了得到对新受试者分类效果良好的模型,需要收集大量新受试者的标记数据,但这往往不现实。本研究针对跨受试者脑电情绪分类提出了一种迁移判别字典对学习(TDDPL)方法。TDDPL方法将不同受试者的数据投影到领域不变子空间中,基于最大均值差异(MMD)策略构建迁移字典对学习。在子空间中,TDDPL学习共享的综合字典和分析字典,搭建从源域(SD)到目标域(TD)的判别知识桥梁。通过最小化每个子字典的重构误差和类间分离项,学习到的合成字典具有判别性,而学习到的低秩编码具有稀疏性。最后,在 TD 中,基于分类器参数、分析字典和投影矩阵构建判别分类器,而无需计算编码系数。在 SEED 和 SEED IV 数据集上验证了 TDDPL 方法的有效性。
通过估计态密度进行量子拓扑数据分析
我们开发了一种基于组合拉普拉斯算子的状态密度 (DOS) 估计的量子拓扑数据分析 (QTDA) 协议。计算图和单纯复形的拓扑特征对于分析数据集和构建可解释的人工智能解决方案至关重要。由于组合缩放,对于具有超过 60 个顶点和高阶拓扑特征的单纯复形,这项任务在计算上变得困难。我们建议通过将底层超图嵌入为有效量子汉密尔顿量并从时间演化中评估其状态密度来完成这项任务。具体来说,我们使用有效汉密尔顿量的 Cartan 分解将传播器组合成量子电路,并使用多保真协议对时间演化状态的重叠进行采样。接下来,我们开发各种后处理例程并实现类似傅里叶的变换以恢复汉密尔顿量的秩(和核)。这使我们能够估计贝蒂数,揭示单纯复形的拓扑特征。我们在无噪声和有噪声的量子模拟器上测试了我们的协议,并在 IBM 量子处理器上运行了示例。我们观察到,即使在没有错误缓解的情况下,所提出的 QTDA 方法对真实硬件噪声的弹性也很大,这显示了近期设备实现的前景,并凸显了基于全局 DOS 的估计器的实用性。
Gröbner 基的量子计算
本文探讨了代数几何的基本工具格罗布纳基的量子计算可行性。计算格罗布纳基的经典方法基于 Buchberger 算法,我们的问题是如何在其中采用量子算法。寻找最大值的量子算法可用于检测多项式的首项,这是计算 S 多项式所必需的。关于格罗布纳基的 S 多项式的约化可以通过表示多项式的矩阵的 Gauss-Jordan 消元法的量子版本来完成。然而,多项式零约化的频繁发生阻碍了量子算法的有效应用。这是因为多项式的零约化发生在非满秩矩阵中,而量子线性系统算法(通过矩阵求逆)对此是不够的,因为众所周知的量子线性求解器(如 Harrow-Hassidim-Lloyd)需要秘密计算特征值的逆。此类算法应在保证矩阵可以求逆的有限情况下使用。例如,从非约化 Gr¨obner 基到约化 Gr¨obner 基的转换就是这种类型的,量子算法肯定可以实现计算的部分加速。关键词——量子计算;量子算法;量子力学;符号计算;Gr¨obner 基;Buchberger 算法;F4 算法,F5 算法,F5C 算法
sq3370通过肿瘤上的点击化学激活细胞毒性药物,并在注射和非注射病变中持续反应
a)用于免疫能力C56BL/6小鼠的合成性MC38双肿瘤研究的治疗示意图。所有肿瘤细胞均在第0天植入。b)b)在第7天开始,在原发性“注射”肿瘤的局部注射生物聚合物,然后进行全身治疗。c)治疗组的Kaplan-Meier生存曲线。d)肿瘤生长曲线显示出注入SQL70生物聚合物(注射肿瘤)的大型原发性肿瘤的平均值±SEM。e至g)蜘蛛图显示了SQ3370,DOX和盐水治疗组中各个远端非注射肿瘤的生长,分别显示了单个非注射肿瘤的肿瘤生长曲线,以每种治疗组的每种肿瘤的初始体积的百分比(在第12天的测量中测量)的肿瘤生长曲线显示为每个治疗组的初始体积的百分比。没有错误栏的数据点。曲线在该组中1只或更多小鼠死后停止,当肿瘤体积达到2000 mm3时死亡或处死。灰色条代表治疗持续时间。肿瘤生长曲线中的统计显着性是由welch每天进行校正的未配对t检验确定的。通过对数秩(壁炉棒)测试确定生存中的统计显着性 *p <0.05; ** p <0.01; *** p <0.001。
最大几何量子熵
首先,回想一下参考文献。[ 24 ] 其中 Hughston、Josza 和 Wootters 给出了给定密度矩阵背后所有可能集合的构造性特征,假设集合具有有限数量的元素。其次,Wiseman 和 Vaccaro 在参考文献中。[ 25 ] 然后通过物理可实现集合的动态激励标准论证了首选集合。第三,Goldstein、Lebowitz、Tumulka 和 Zanghi 挑选出高斯调整投影 (GAP) 测度作为热力学和统计力学环境中密度矩阵背后的首选集合 [ 26 ]。第四,Brody 和 Hughston 在几何量子力学中使用了最大熵的一种形式 [27]。HJW 定理。在技术层面上,对于我们的目的而言,最重要的结果之一是 Hughston-Josza-Wootters (HJW) 定理,该定理已在文献 [ 24 ] 中证明,现在我们对其进行总结。考虑一个有限维希尔伯特空间 H S 的系统,该系统由秩为 r 的密度矩阵 ρ 描述:ρ = P r j =1 λ j | λ j ⟩⟨ λ j | 。我们假设 dim H S := d S = r ,因为 d S > r 的情况很容易通过将 H S 限制在由 ρ 的图像定义的 r 维子空间中来处理。然后,可以通过与具有 d S 个正交向量作为列的 d × d S 矩阵 M 进行线性混合,从 L ( ρ ) 生成具有 d ≥ d S 个元素的通用集合 e ρ ∈E ( ρ )。然后,e ρ = { p k , | ψ k ⟩} 由以下公式给出:
量子卡方断层扫描和互信息测试
量子态断层扫描(从 𝑛 个副本中学习 𝑑 维量子态)是量子信息科学中一项普遍存在的任务。它是从 𝑛 个样本中学习 𝑑 结果概率分布的经典任务的量子类似物。更详细地说,目标是设计一种算法,给定某个(通常是混合的)量子态 𝜌 ∈ C 𝑑 × 𝑑 的 𝜌 ⊗ 𝑛,输出一个估计值 2 ̂︀ 𝜌(的经典描述),该估计值以高概率“𝜖 接近”𝜌。主要挑战是将样本(副本)复杂度 𝑛 最小化为 𝑑 和 𝜖(有时还有其他参数,例如 𝑟 = 秩 𝜌 )的函数。我们还将关注设计仅进行单次(而不是集体)测量的算法的实际问题。指定量子断层扫描任务的一个重要方面是“𝜖-close”的含义;即,判断算法估计的损失函数是什么。有很多自然的方法可以测量两个量子态的发散度——甚至比两个经典概率分布的发散度还要多——并且所选择的精确测量方法会对必要的样本复杂度以及最终估计对未来应用的效用产生很大的影响。本文的主要目标是展示一种新的断层扫描算法,该算法实现最严格的准确度概念(Bures)𝜒 2 -发散度,同时具有与以前使用不忠诚度作为损失函数的算法基本相同的样本复杂度。然后,我们给出了一个应用,即量子互信息测试问题,这关键依赖于我们实现关于𝜒 2 -发散度的有效状态断层扫描的能力。
10122.pdf
AIM:左心室(LV)肥大(LVH)是动脉高血压(AH)和12铅心电图(ECG)的常见并发症(ECG)的初步评估。该研究的目的是比较LVH的四个ECG衍生标准的相关性和左心房(LA)前后直径的相关性,并通过超声心动图评估LVH,并以左心室质量(LVM)指数(LVMI)表示,以寻找最准确的LVH PRELIMARIMALIMY指标。方法:该研究包括61名AH [年龄(年龄)69±10,17名女性]和27名没有AH的受试者,(年龄40±9,10名女性)通过12铅ECG和胸腺超声心动图(TTE)评估。作为基于ECG的LVH Sokolow-Lyon指数(SLI),Cornell电压(CV),Cornell产品(CP)和Romhilt-Estes点得分(RES)系统的标准。ECG指数和LA直径与LVMI相关,并比较了相关系数。结果:在ECG-LVH指标中,SLI显示了与LVMI [秩相关系数(RHO)= 0.38,p <0.0001]的最接近的相关性,其次是CV和CP,RHO = 0.33,P = 0.002,RHO = 0.002和Rho = 0.32,P = 0.002,而不是相关的。发现LA直径的最强相关性与RHO = 0.73和P <0.0001的LA直径相关,显示女性的相关性甚至更强 - 男性的Rho = 0.8(p <0.0001)与Rho = 0.65(p <0.0001)。在多元分析中,LA是LVMI增加的唯一独立预测指标,R
使用拉普拉斯正则化 Schatten p范数最小化从头预测药物-靶标相互作用
在制药科学中,药物发现的一个关键步骤是识别药物-靶标相互作用 (DTI)。然而,只有一小部分 DTI 经过了实验验证。此外,通过传统的生化实验来捕捉药物和靶标之间的新相互作用是一个极其费力、昂贵且耗时的过程。因此,设计用于预测潜在相互作用的计算方法来指导实验验证具有实际意义,特别是对于从头情况。在本文中,我们提出了一种新算法,即拉普拉斯正则化的 Schatten p 范数最小化 (LRSpNM),用于预测新药物的潜在靶标蛋白和没有已知相互作用的新靶标的潜在药物。具体而言,我们首先利用药物和靶标相似性信息来动态地预填充部分未知的相互作用。然后基于相互作用矩阵低秩的假设,我们使用 Schatten p 范数最小化模型结合拉普拉斯正则化项来提高新药/新靶点案例的预测性能。最后,我们通过一种高效的交替方向乘子算法对 LRSpNM 模型进行数值求解。我们在五个数据集上评估了 LRSpNM,大量的数值实验表明 LRSpNM 比五种最先进的 DTI 预测算法具有更好、更稳健的性能。此外,我们对新药和新靶点预测进行了两个案例研究,这表明 LRSpNM 可以成功预测大多数经过实验验证的 DTI。
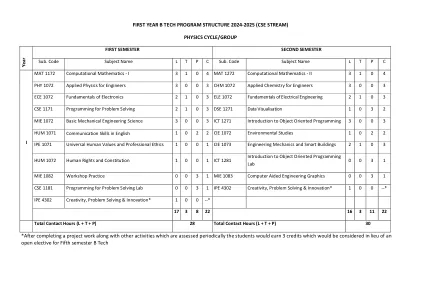
第一年 B TECH 课程结构 2024- ...
用数值方法求解方程。• CO5:应用插值概念求解数值微分和积分问题。教学大纲:矩阵代数:基本列变换和行变换、通过基本行运算求逆矩阵、矩阵的梯形和秩、线性方程组:一致性、高斯消元法、高斯-乔丹法、雅可比法和高斯-赛德尔法求解、特征值和特征向量:基本性质、谱矩阵分解、对角化、矩阵的幂。向量空间:向量概念向高维的推广、广义向量运算、向量空间和子空间、线性独立性和跨度、基。内积空间和 Gram-Schmidt 正交化过程。线性变换。微分方程及应用:一阶和高阶线性微分方程。用逆微分算子、参数变分法和待定系数法求解齐次和非齐次线性方程。代数和超越方程的解:参数曲线的追踪:摆线和相关曲线。二分法、试位法、牛顿-拉夫森法。用牛顿-拉夫森法求解非线性方程组。插值:有限差分和除差分。牛顿-格雷戈里和拉格朗日插值公式。牛顿除差插值公式。离散数值微分、数值积分:梯形法则、辛普森 1/3 法则和辛普森 3/8 法则。常微分方程的数值解:泰勒级数法、修正欧拉法、龙格-库塔法。参考书:
2025年实习项目
实习项目 2025 珍妮·库尔特 研究远非平衡态电子-声子流体动力学输运 在某些条件下,某些材料中的热量和电荷输运可以用流体动力学方程描述。近期研究将电子的稳态流体动力学方程[1]与声子的粘性热方程统一起来,得到了一组更通用的“粘性热电方程”,描述了电子和声子协同产生流体动力学效应的状态。VTE是在接近平衡态的稳态下推导出来的。本项目将VTE扩展到远非平衡态输运现象,这些现象出现在i)导致响应延迟的高频扰动,以及ii)驱动弹道输运和流体动力学输运耦合的空间不均匀性。本项目将涉及理论开发以及扩展Phoebe程序包[3]的计算工作。[1] Gurzhi. Sov. Phys. Uspekhi 11, 255 (1968) [2] Simoncelli, Marzari, Cepellotti, PRX 10, (2020)。[3] https://github.com/phoebe-team/phoebe Olivier Gauthé 有限温度下的多体局部化 多体局部化 (MBL) 是一种有趣的现象,出现在强无序的相互作用量子系统中 [1]。这样的系统在淬火后不会热化,并且会在很长一段时间内保留初始信息。这种现象可以在具有随机局部场的一维自旋链中观察到。张量网络是一种成熟的方法,用于模拟依赖于高维数据低秩近似的强关联系统。使用