XiaoMi-AI文件搜索系统
World File Search System难以解决
关于求解条件数中运行时间二次改进的正定量子线性系统类
用于解决量子线性系统 (QLS) 问题的量子算法是近年来研究最多的量子算法之一，其潜在应用包括解决计算上难以解决的微分方程和提高机器学习的速度。决定 QLS 求解器效率的一个基本参数是 κ，即系数矩阵 A 的条件数，因为自从 QLS 问题诞生以来，我们就知道，在最坏情况下，运行时间至少与 κ 呈线性关系 [1]。然而，对于正定矩阵的情况，经典算法可以求解线性系统，运行时间扩展为 √κ，与不确定的情况相比，这是一个二次改进。因此，很自然地会问 QLS 求解器是否可以获得类似的改进。在本文中，我们给出了否定的答案，表明当 A 为正定时，求解 QLS 也需要与 κ 呈线性关系的运行时间。然后，我们确定了可以规避此下限的正定 QLS 的广泛类别，并提出了两种新的量子算法，其特点是 κ 的二次加速：第一种基于有效实现 A − 1 的矩阵块编码，第二种构建形式为 A = LL † 的分解来预处理系统。这些方法适用范围广泛，并且都允许有效地解决 BQP 完全问题。
混合碰撞避免方法
摘要：在此手稿中，我们考虑轨迹计划和控制中的避免障碍任务。这些任务的挑战在于难以解决最佳控制问题（OCP）的非convex纯状态约束。强化学习（RL）提供了处理障碍限制的更简单方法，因为只需要建立反馈功能。尽管如此，事实证明，我们经常获得持久的训练阶段，我们需要大量数据来获得适当的解决方案。一个原因是RL通常没有考虑到基本动力学的模型。相反，此技术仅依赖于数据中的信息。为了解决这些缺点，我们在本手稿中建立了一种混合和分层方法。虽然经典的最佳控制技术处理系统动力学，但RL专注于避免碰撞。最终训练的控制器能够实时控制动态系统。即使动态系统的复杂性对于快速计算或需要加速训练阶段的复杂性太高，我们也通过引入替代模型来显示一种补救措施。最后，总体方法应用于在赛车轨道上引导汽车，并通过其他移动的汽车进行动态超车。
通过 MaxSAT 进行量子比特映射和路由 - cs.wisc.edu
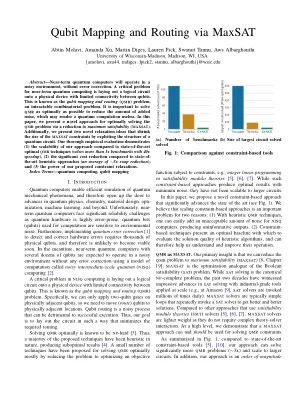
摘要 — 近期量子计算机将在嘈杂的环境中运行，且无法进行纠错。近期量子计算的一个关键问题是将逻辑电路布置到量子比特之间连接有限的物理设备上。这被称为量子比特映射和路由 ( QMR ) 问题，是一个难以解决的组合问题。尽可能以最优方式解决 QMR 非常重要，以减少增加的噪声量，因为噪声可能会导致量子计算变得毫无用处。在本文中，我们提出了一种通过简化为最大可满足性 ( MAXSAT ) 来最优解决 QMR 问题的新方法。此外，我们提出了两个新颖的松弛思想，通过利用量子电路的结构来缩小 MAXSAT 约束的大小。我们彻底的实证评估表明：(1) 与最先进的最优 QMR 技术相比，我们的方法具有可扩展性（解决了 3 倍以上的基准问题，速度提高了 40 倍）；(2) 与最先进的启发式方法相比，成本显著降低（平均减少 ∼ 5 倍交换）；(3) 我们提出的约束放松的强大功能。索引术语 — 量子计算、量子比特映射
吸湿排汗
芯吸和泵送 多年来，多孔金属已演变成许多难以解决的工艺问题。其中之一就是泵送和/或芯吸的使用。Mott 的多孔烧结金属是从航空航天到消费用途的许多应用的完美选择。 芯吸 具有非常均匀孔隙率的多孔金属结构将通过多孔金属结构将液体从流体储存器泵送液体并将液体施加到所需位置。由于均匀的孔分布和孔径，毛细管粘附发生在多孔结构内。 优点 无活动部件 长免维护使用寿命 清洁度 提供均匀的流动 连续操作 高强度、抗冲击 耐高温 过滤，为应用提供清洁流体 烧结金属用于液体冷却系统中的泵 多孔金属也可用于封闭的再循环系统。多孔材料在此系统中充当主泵。该系统的工作原理与芯吸相同，不同之处在于系统是完全封闭的。该系统的泵头压力可高达 30” H2O，具有这种性能的多孔金属适用于各种冷却应用。冷却应用航空航天卫星宇航员太空服冷却微电子电力电子开关整流器无功元件变压器
高性能和创新计算 (HPIC) 报告...
由欧洲航天局 (ESA) 牵头的地球观测量子计算 (QC4EO) 计划 1 旨在探索量子计算与地球观测 (EO) 之间的潜在协同作用。该计划旨在确定有前景的用例，聚集两个社区，并为量子计算进步带来的机遇做好准备。量子计算有可能通过利用量子现象来提高性能、降低计算成本并解决 EO 中以前难以解决的问题。为了进一步探索高性能计算 (HPC) 和 EO 的交集，组织了 HPC 和创新计算 (HPIC) 研讨会。研讨会于 2023 年 10 月 12 日在意大利弗拉斯卡蒂的 ESA 地球观测中心 ESRIN 举行，汇集了来自 HPC 和 EO 领域的专家，讨论它们的相互联系、未来前景和挑战。此次活动的演讲嘉宾来自欧洲 HPC 中心，例如 FZ Julich、Cineca 和 CSC，以及来自 IQM 计算机公司、帕多瓦大学和 ESA 的代表。研讨会现场有 25 名与会者，另有 75 名参与者在线参加。本报告总结了各位演讲嘉宾的演讲和随后的讨论。
通过在量子计算机上准备热状态来研究伊辛模型的临界行为
随着量子器件和量子算法的发展，量子计算机可以解决经典计算机难以解决的问题。量子计算机已经成功应用于量子化学、凝聚态物理和格子场论等许多领域（例如参见参考文献 [ 1 – 7 ]）。随着量子比特数量的增加和量子器件保真度的提高，我们可以处理更现实的物理模型，探索量子计算机的潜力。作为一个应用示例，本文用量子算法在不同温度下准备 Ising 模型的热态，包括接近临界温度和低温区域的点。为了证明我们方法的可行性，我们将所选物理量的量子模拟结果与经典模拟结果进行了比较。已经提出了许多算法来使量子计算机能够准备热态。这些方法包括量子热动力学方法，其中目标系统与处于平衡状态的溶液耦合 [8]；基于热场双态的变分量子算法 [9,10]；以及许多量子虚时间演化 (QITE) 算法，例如利用 Hubbard-Stratonovich 变换的算法 [11]、基于变分假设的 QITE (QITE-ansatz) [12]、基于测量的 QITE (QITE-measure) [13]，以及通过执行坐标优化的 QITE [14]。我们的研究范围集中在有噪声的中尺度量子 (NISQ) 设备的使用 [15,16]。考虑到量子
利用约瑟夫森量子退火炉的开发...
按照摩尔定律（芯片上晶体管的数量每 18 个月就会翻一番 [1]），包括 CPU 在内的通用处理器的性能每年都在提高，而价格和功耗却在下降。由于功耗限制，工作频率和单线程处理性能已几乎达到极限。这些限制导致了多核处理器的发展，而多核处理器的加速也受到顺序执行的程序数量的限制。因此，加速已在适当的地方利用了专门的架构，例如 GPU。虽然 GPU 不能像 CPU 那样执行通用处理，但它们可以执行大量并行简单操作，这对机器学习非常有用。量子计算机作为一种专门的架构，因其能够解决传统计算机难以解决的问题而备受关注。传统计算机的信息处理单元（比特）只有 0 或 1 两种状态，而量子计算机则由可以叠加 0 和 1 状态的量子比特（量子位）组成。这些计算机可以利用量子力学的特性，例如状态叠加、量子隧穿和量子纠缠。量子计算机大致可分为两类：基于门的量子计算机 [2] 和量子退火机 [3]。基于门的量子计算机可以利用量子比特状态叠加（2 个 𝑛 量子比特的状态）之间的干涉效应极快地计算特定问题，并且向上兼容
脊柱外科人工智能和机器学习的应用
预测模型的开发并不是脊柱外科领域的新概念。几十年来，外科医生一直依靠各种统计分析来确定并发症的风险因素，希望能够创建一个有效的模型。一种流行的技术是使用多元逻辑回归 (LR)，它可以为感兴趣的结果产生独立变量的优势比。这种分析的优势包括相对容易解释和应用。然而，预测模型的一个重要限制是所包含的预测变量数量有限。此外，这些传统分析本质上是静态的，假设输入和输出变量之间存在“线性”关系，并且在引入新数据时可能难以解决患者特定需求的复杂性。在过去十年中，医疗保健提供者通过电子病历的数字化获得了大量患者信息。因此，人工智能 (AI) 和机器学习 (ML) 已成为实施更准确和更通用的预测模型的潜在解决方案的中心。人工智能和机器学习越来越受青睐的主要原因包括能够快速处理大量数据、创建适应新数据的模型以及理解传统回归模型可能无法理解的复杂非线性关系。脊柱研究已经显示出机器学习方法的潜力
解决燃气轮机机组的“Y”型需求冲击……
Paul Simshauser ♣♠ 和 Joel Gilmore ♣ 摘要 澳大利亚电力系统规划人员的长期任务是确定与淘汰国家电力市场 (NEM) 煤炭机组相关的结构调整路径。系统规划模型力求在可靠性约束下以最低成本实现这一目标。这涉及部署低成本间歇性风能和太阳能资源以及可调度、灵活的“稳固”资产组合。因此，煤炭的能源生产角色被可再生能源取代，而稳固职责则被短时电池、中时抽水蓄能和最后一道防线——燃气轮机取代。事实证明，稳固资产的组合至关重要。在本文中，我们研究了后煤炭时代的 12 个（匿名）电力市场模型预测，发现在关键的冬季，所有这些预测都出人意料地严重依赖燃气轮机。使用东澳大利亚天然气市场的动态部分平衡模型，我们测试了新兴燃气轮机机组似乎带来的需求冲击的严重程度。偶发性需求冲击似乎难以解决，尤其是当电池和抽水蓄能电站在总发电组合中“权重不足”时。政策制定者有足够的时间有序应对。关键词：天然气市场、燃气轮机、可再生能源、稳固产能。JEL 代码：D52、D53、G12、L94 和 Q40。
![arXiv:1907.09278v2 [cs.AI] 2021 年 3 月 1 日](/simg/g:\will\search\icon\source\b\b56249f47d3400dc780a2a5a6b1e7a2371ddf6ce.png)
arXiv:1907.09278v2 [cs.AI] 2021 年 3 月 1 日
在复杂环境中做出决策是人工智能 (AI) 面临的一个关键挑战。涉及多名决策者的情况尤其复杂，导致原则性解决方法在计算上难以解决。人工智能领域的大量研究试图通过提炼交互的本质来缓解这一问题：一个代理的策略如何影响另一个代理？如果我们能够找到这种影响的更紧凑表示，这可以帮助我们处理复杂性，例如通过搜索影响空间而不是策略空间。然而，到目前为止，这些影响概念的适用性仅限于特殊的交互情况。在本文中，我们形式化了基于影响的抽象 (IBA)，它有助于消除潜在状态因素而不会造成任何价值损失，适用于一类非常普遍的问题，即分解部分可观随机博弈 (fPOSG)。一方面，这概括了现有的影响力描述，因此可以作为改进可扩展性和其他复杂多智能体决策见解的基础。另一方面，由于其他智能体的存在可以看作是单个智能体设置的概括，我们对 IBA 的公式也为单个智能体在抽象下的决策提供了足够的统计数据。我们还详细讨论了与这些先前研究的关系，确定了这些方法的新见解和解释。通过这些方式，本文加深了我们对广泛的顺序决策设置中的抽象的理解，为一大类问题的新方法和算法提供了基础。