机构名称：
¥ 1.0
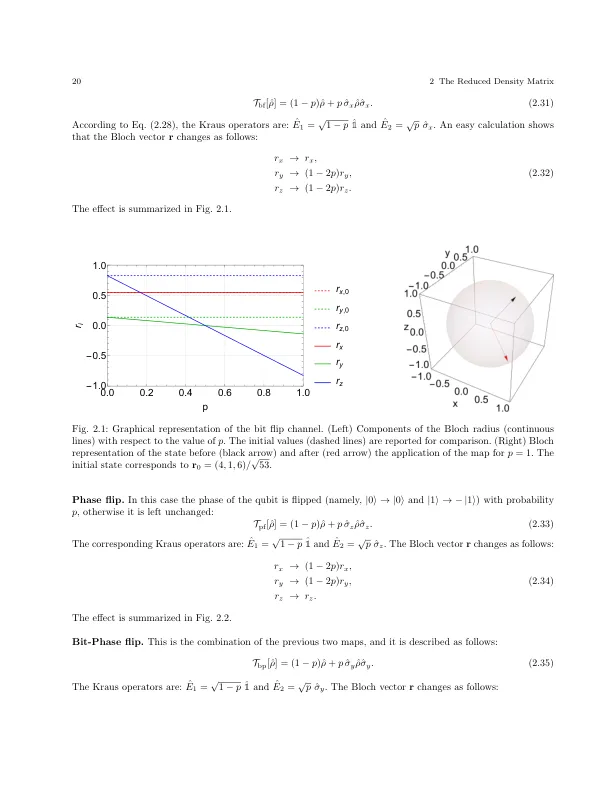
考虑一个开放的量子系统，其相关的希尔伯特空间 H 的维数为 N 。设 ˆ ⇢ 描述其在给定初始时间的状态，设 ˆ ⇢ 0 为某个固定时间后的状态。设 T : B ( H ) ! B ( H ) 为连接这两个状态的映射。第一个观察结果是映射 T 必须是线性的。其原因在于第 1.1 节中介绍的密度矩阵的物理意义，以及“无知线性传播”的座右铭，这在经典和量子情况下都是有效的。如果一个系统处于状态 | 1 i 的概率为 p 1 ，处于状态 | 2 i 的概率为 p 2 ，并且如果 | 1 i 演变为 | 0
2.2 量子操作和 Kraus-Stinespring 定理
主要关键词
相关文件推荐
