机构名称：
¥ 1.0
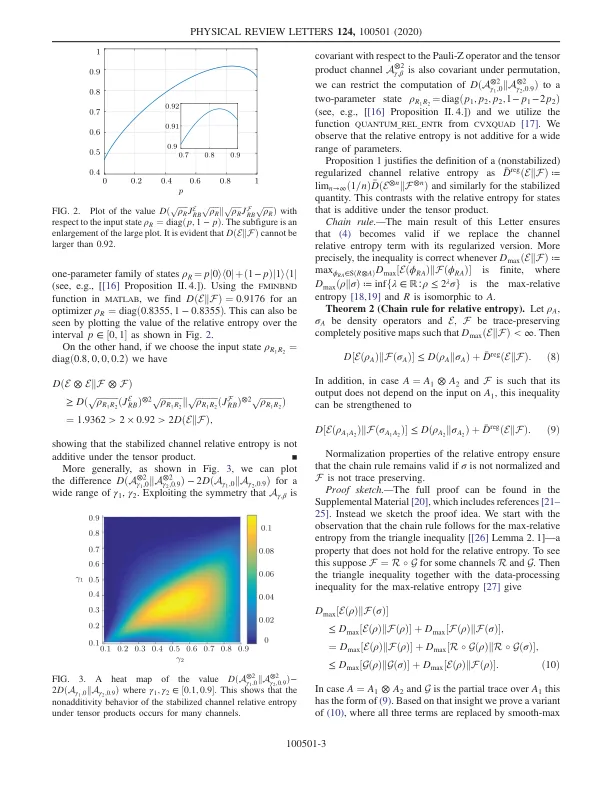
其中 D reg ð E k F Þ ≔ lim n → ∞ ð 1 =n Þ D ð E ⊗ nk F ⊗ n Þ 。语句 (5) 意味着第一个不等式可以是严格的。根据摊销通道相对熵 (7) 的定义，这直接意味着 (6)。因此还需证明 (5)。为此，我们构造一个满足 (5) 的量子位上的两个迹保持完全正映射 E 和 F 的示例。考虑广义振幅阻尼通道 A γ ; β ð ρ Þ = P 4 i = 1 A i ρ A † i，其中 γ ; β ∈ ½ 0; 1 使用 Kraus 运算符 A 1 ¼ ffiffiffiffiffiffiffiffiffiffiffi 1 − β p ðj 0 ih 0 j þ ffiffiffiffiffiffiffiffiffiffi 1 − γ pj 1 ih 1 jÞ , A 2 ¼ ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi γ ð 1 − β Þ pj 0 ih 1 j , A 3 ¼ ffiffiffi β p ð ffiffiffiffiffiffiffiffiffiffi 1 − γ pj 0 ih 0 jþ j 1 ih 1 jÞ 和 A 4 = ffiffiffiffiffi γβ pj 1 ih 0 j 。对于两个通道 E = A 0.3;0 和 F = A 0.5;0.9，它们对应的 Choi 矩阵根据计算基础由下式给出
量子相对熵的链式法则 - 方昆
主要关键词
相关文件推荐
