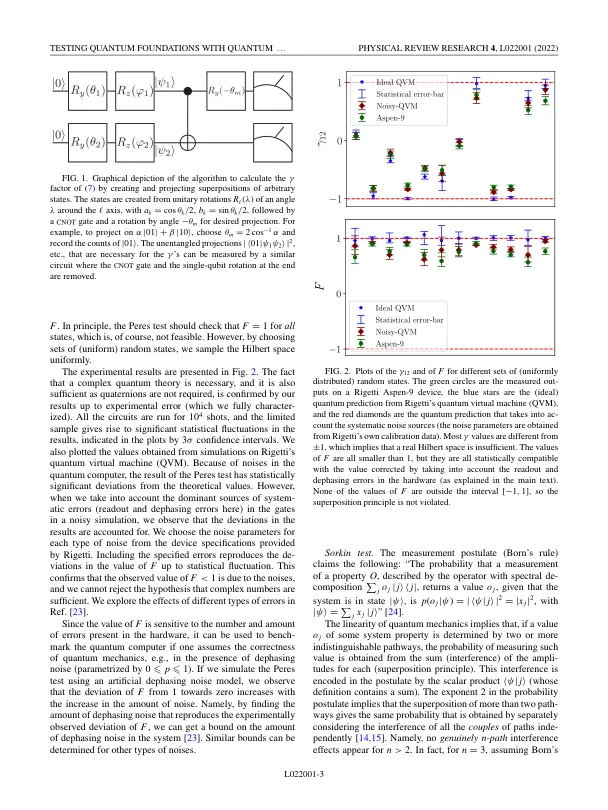
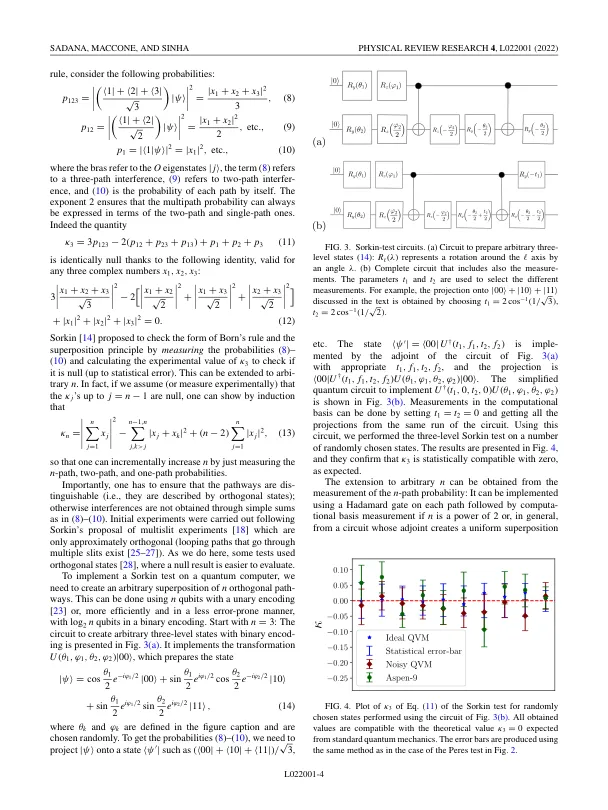
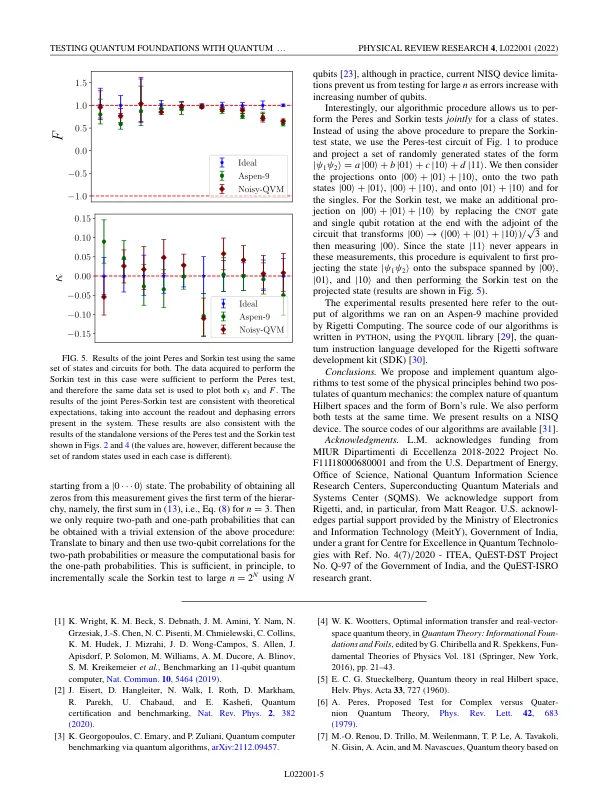
机构名称:
¥ 1.0
物理学是实验性的,因此所有物理理论的假设都是基于实验的。在这里,我们建议使用量子计算机直接对量子力学的两个假设进行实验测试。在理想情况下,假设硬件完美,它们特别适合此目的,因为它们是具有大量自由度的量子系统。相反,在非理想情况下,即噪声中尺度量子 (NISQ) 设备,可以假设量子力学有效,并使用这些测试对 [ 1 – 3 ] 深量子级别的设备进行基准测试,因为它们基于理论的基础(假设)。换句话说,假设硬件完美,可以测试量子力学;假设量子力学,可以测试硬件。放宽这两个假设,可以执行自洽性检查来测试两者。我们提出了两个这样的实验测试:我们为 Peres 和 Sorkin 测试提供算法和量子机器代码,并在 Rigetti 量子计算机上运行它们。第一个实验是对量子力学状态公设(即叠加原理)的检验,该公设认为量子态存在于复希尔伯特空间中。原则上,可以设想基于实数[ 4 , 5 ]、复数或四元希尔伯特空间[ 6 ]的量子力学:选择基于实验结果,例如Peres的实验;另见参考文献[ 7 – 12 ]。复数是必要(且充分)的事实具有有趣的含义,例如,它意味着量子态是局部可区分的[ 13 ],并且它与某些量子现象的局部性有关[ 7 ]。第二个实验测试由Sorkin [ 14 ]提出,是对玻恩公设的检验。玻恩规则表明量子概率是
使用量子计算机测试量子基础
主要关键词