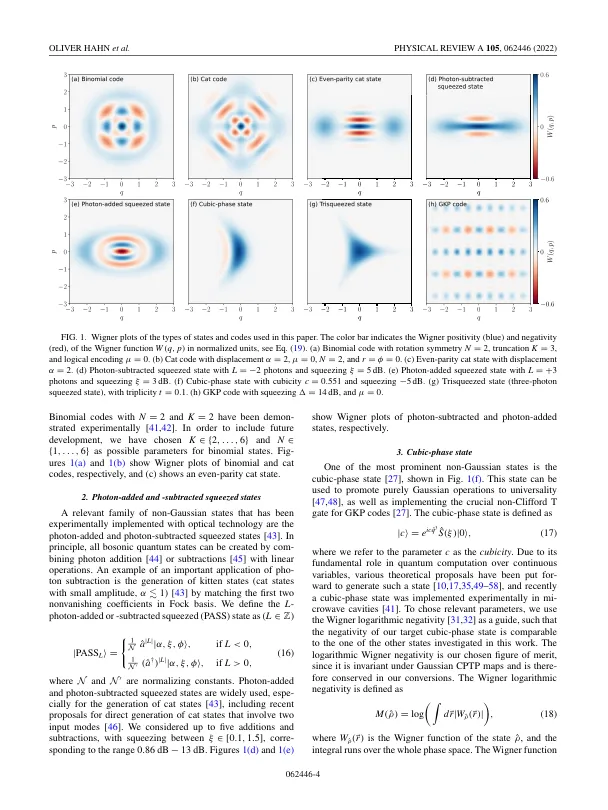
机构名称：
¥ 1.0
在连续变量量子技术的背景下，高斯状态和操作通常被视为自由可用的，因为它们相对容易通过实验获得。相比之下，非高斯状态的生成以及非高斯操作的实施则带来了重大挑战。这种分歧促使人们引入非高斯性的资源理论。对于任何资源理论，确定资源之间的自由转换协议（即非高斯状态之间的高斯转换协议）具有实际意义。通过系统的数值研究，我们通过任意确定性的一对一模式高斯映射解决了实验相关的单模非高斯状态之间的近似转换。首先，我们表明，对于有限能量，猫状态和二项式状态大致等效，而这种等效性以前仅在无限能量极限下才为人所知。然后，我们考虑从光子增加和光子减少的压缩态生成猫态，通过引入额外的压缩操作来改进已知方案。我们开发的数值工具还允许人们设计出三压缩态到立方相态的转换，超越之前报道的性能。最后，我们确定了其他各种不可行的转换。
非...的确定性高斯转换协议
主要关键词
相关文件推荐
