XiaoMi-AI文件搜索系统
World File Search System二维材料中的相变 - 李巨课题组
大量核素和电子的自组织导致物质出现不同相。相代表一种可以在空间上无限复制的组织方式,其特性会随着外场的变化而不断变化,与其他相不同。因此,当材料经历相变时,某些系统特性会发生变化。相变的一般特征是,它要么涉及根据相变的朗道范式 1 – 3 的序参量的不连续性,要么涉及拓扑不变量的变化 4、5。发现、表征和控制物质的不同相是凝聚态物理学和材料科学的核心任务。特别是,对二维系统中相变的研究在促进我们对相变的理解方面发挥了至关重要的作用(图 1)。 2D 材料 6 – 10 是可以在两个方向上无限复制,但在第三个方向上具有原子级厚度的物质。例如,单层 MoS 2 的厚度为 6.7 Å,在通过机械剥离 6 制备的实验室样品中,平面内厚度通常为微米,因此,其长宽比为 ~10 3 或更大。为了进行比较,一张典型的 A4 大小的纸(~100 μm × 29.7 cm × 21 cm)的长宽比也相似,为 ~10 3 。虽然 2D ↔ 3D/1D 相变无疑是有趣的讨论主题,但在这里,我们重点关注 2D → 2D 转变。最早对 2D 相变的研究大多是理论上的;例如二维 Ising 自旋模型的精确解 11 、 Hohenberg–Mermin–Wagner 定理的提出 12 , 13 以及 Kosterlitz–Thouless 转变的发现 14 , 15 (图 1 )。20 世纪 80 年代初,半导体技术的进步使得人们能够实验研究半导体界面和强磁场下的二维电子系统,从而带来了突破性的
经典方差是否应作为基本测量...
摘要 - 由于测量结果并不比其不确定度更好,因此指定不确定度是计量学的一个非常重要的部分。人们倾向于相信物理学中的基本常数随时间不变,并且它们是建立国际系统 (SI) 标准和计量学的基础。因此,在最先进的水平上明确指定这些物理不变量的不确定性应该是计量学的主要目标之一。但是,通过观察某些物理量的行为,我们可能会扰乱标准,从而引入不确定性。一系列观测中的随机偏差可能是由测量系统、环境耦合或标准中的固有偏差引起的。由于这些原因,并且由于相关随机噪声在自然界中与不相关随机噪声一样普遍存在,因此普遍使用经典方差和均值标准差可能会混淆而不是澄清有关不确定性的问题;即,这些测量仅适用于随机不相关偏差(白噪声),而白噪声通常是观察到的偏差频谱的子集。如果事实上该系列不是随机和不相关的,即没有白色频谱,那么由于测量是在不同时间进行的,因此系列中每个测量都是独立的假设应该受到质疑。在本文中,频率标准、标准电压电池和量块的研究提供了长期随机相关时间序列的例子,这些时间序列表明行为不是“白色”(不是随机和不相关的)。本文概述并说明了一种简单的时域统计方法,该方法为幂律谱提供了一种替代估计方法,可用于大多数重要的随机幂律过程。了解频谱可以在存在相关随机偏差的情况下提供更清晰的不确定性评估,所概述的统计方法还为白频谱提供了一个简单的测试,从而使计量学家能够知道使用经典方差是否合适或是否要结合更好的不确定性评估程序,例如,如本文所述。
迈克尔·保罗·兰德里简介
研究文章 12. 与 Y. Minsky 和 S. Taylor 一起研究同步通用圆 25 页。arXiv:2412.06986。 11. 与 Y. Minsky 和 S. Taylor 一起研究横向曲面和伪 Anosov 流,已提交 2024 年。48 页。arXiv:2406.17717。 10. 与 CC Tsang 一起研究端周期映射、分裂序列和分支曲面,几何与拓扑,即将出版。144 页。arXiv:2304.14481 9. 与 Y. Minsky 和 S. Taylor 一起研究通过伪 Anosov 流实现的端周期映射,已提交 2023 年。50 页。arXiv:2304.10620。 8. 与 Y. Minsky 和 S. Taylor 一起研究流动、增长率和转向多项式,遍历理论和动力系统,第 43 卷,号。 9,第 3026-3107 页。2023. 7. 与 Y. Minsky 和 S. Taylor 合作的用于转向三角剖分的多项式不变量欧洲数学学会杂志第 6 卷,第 2 期,第 731-788 页。2024. 6. 转向三角剖分和 Thurston 范数:与同位素的同源性数学进展,第 396 卷,论文 108102,2022 年,53 页。5. 稳定环和几乎横向曲面群、几何和动力学第 17 卷,第 1 期,第 35-75 页。2023. 4. 来自转向三角剖分的绷紧分支曲面代数和几何拓扑18 1089-1114,2018。3. On symplectic capacities of toric domains with M. McMillan and E. Tsukerman Involve Vol. 8, pp. 665-676, 2015。2. Knotprojections with a single multi-crossing with Adams, Crawford, DeMeo, Lin, Montee, Park, Venkatesh, and Yhee Journal of Knot Theory and its Ramifications Vol. 24 (3), 2015。
JB HI 特别专题“脑信号和神经成像的模糊系统和计算方法:
鉴于处理从神经成像模式获得的脑信号所面临的重大挑战,模糊集和系统已被提出作为分析脑活动的有用且有效的框架,以及实现脑与外部设备(脑机/机接口)之间的直接通信途径。虽然人们对这些问题的兴趣越来越大,但模糊系统的贡献因应用领域而异。一方面,考虑到脑活动的解码,处理不确定性的高级计算智能方法(如模糊集和系统)代表了一种极好的工具,可以克服处理极度嘈杂的信号的挑战,这些信号很可能受到非平稳性、不变量和泛化能力差的影响。另一方面,就神经科学研究而言,可能性和模糊性同样被用于测量突触、神经元和大脑区域或区域之间的平滑整合。在此背景下,拟议的特刊旨在建立一个专门的论坛,作为计算智能研究人员的媒介,他们希望利用模糊系统和模糊逻辑等先进技术来模拟和表达对脑信号和神经成像数据分析的不确定性。任何与神经科学相关的领域,如计算神经科学、脑机接口、神经科学、神经信息学、神经人体工程学、计算认知神经科学、情感神经科学、神经生物学、脑映射、神经工程和神经技术都是合适的。本期特刊重点介绍在不同知识领域研究的模糊系统和应用于脑信号和神经成像的计算方法的最新进展、挑战和未来前景。因此,我们邀请研究人员为本期特刊贡献原创作品,利用脑信号和神经成像中使用计算和数学技术的最新方法,并解决开发用于各种临床应用的专用系统的挑战,同时提出未来发展的新想法和方向。感兴趣的主题包括但不限于以下内容:
arXiv:2311.11218v1 [quant-ph] 2023 年 11 月 19 日
层论的语境定义对我们理解语境起到了重要作用,因为它为直观的语境概念提供了精确的数学结构。层论框架最早由 Abramsky 和 Brandenburger [11, 13] 提出,他们在测量场景中定义了事件和分布,并确定了这些概念的层结构。在这里,我们可以将全局分布与隐变量模型联系起来,该模型因无法解释量子理论的独特特征而闻名。Abramsky、Barbosa 和 Mansfield [16] 进一步探讨了语境的一种度量。这项工作开辟了在给定量子场景中量化语境的方法。随后同调方法对语境的研究也为在给定测量场景中观察语境提供了重要的方法。 Abramsky、Mansfield 和 Barbosa [12] 提出了基于ˇ Cech 上同调不变量的方法,该方法利用层上同调的强大工具来检测经验模型中的语境性。Okay、Roberts、Bartlett 和 Raussendorf [21] 的提议建立了识别语境性的拓扑方法,该方法有可能提供更精细的分析,尽管必须考虑额外的拓扑结构。Aasnæss [18] 将这些方法联系起来,通过将论据从一种转化为另一种,补充了每种方法的通用性和完整性。另一方面,同一研究小组还描述了一种更强形式的语境性,即全有与全无 (AvN) 论据。Abramsky 等人 [14, 15] 参考 Mermin [9, 10] 的观察,将量子信息系统中的逻辑不一致性形式化为 AvN 论证。在 Aasnæss [18] 的著作中,这种语境性也被看作是上同调群的一个障碍。虽然层论框架为 MBQC 和浅层电路的量子优势提供了论证基础,但应用的最后一个案例,即参考文献 23 和 24,可以追溯到 Kochen 和 Specker 关于形式化语境性的框架,即所谓的封闭子理论中的语境性。这个概念似乎用
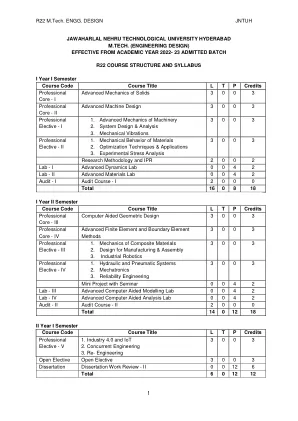
R22 工程技术硕士设计 JNTUH
确定施加载荷的位置点,以避免航空航天应用中使用的薄截面发生扭曲。 理解区分曲梁中中性轴和质心轴的概念。 理解为分析受扭转的非圆形杆而开发的类比模型,以及分析滚动体之间产生的应力和三维物体中的应力。 UNIT-I:应力分析:点的应力状态、任意平面上的应力分量、主应力、应力不变量、莫尔圆、最大剪切平面、八面体应力、平面应力状态、平衡微分方程、边界条件。应变分析:点附近的变形、点的应变状态、剪应变分量的解释、应变和主应变的变换、兼容条件。平面应变状态。线性应力-应变-温度关系:内能密度和互补内能密度。各向异性、正交各向异性和各向同性弹性的胡克定律。各向同性材料的热弹性方程 UNIT-II 剪切中心:轴对称和非对称截面的弯曲轴和剪切中心-剪切中心。薄壁截面的剪切应力、箱梁的剪切中心非对称弯曲:非对称弯曲梁的弯曲应力、非对称弯曲导致的直梁挠度。 UNIT-III:曲梁理论:温克勒-巴赫周向应力公式 – 局限性 – 校正系数 – 曲梁的径向应力 – 闭环承受集中和均匀载荷 – 链环中的应力。第四单元:扭转:线性弹性解,一般棱柱形杆——实心截面,如圆形、椭圆形、三角形和矩形,普朗特弹性膜(皂膜)类比;窄矩形截面,空心薄壁扭转构件,多连通截面。第五单元:接触应力:介绍,确定接触应力的问题,接触应力解所基于的假设;主应力表达式;计算接触应力的方法,点接触物体的挠度;两个物体在窄矩形区域接触的应力(线接触)垂直于面积的载荷,两个物体线接触的应力,垂直于和切向于接触面积的载荷。
社论:神经成像的计算方法
计算方法已被提出作为分析大脑活动的有用且有效的框架。鉴于处理从神经成像模式获得的大脑信号存在重大困难,在大脑和外部设备(脑机接口)之间建立直接通信通路是必要的。虽然人们对这些问题的兴趣越来越大,但模糊系统的贡献因应用领域而异。在解码大脑活动时,处理可能受非平稳性、不变量和泛化不良影响的极其嘈杂的信号是一项重大挑战。然而,处理不确定性的高级计算智能方法(如模糊集和系统)是克服这一挑战的绝佳工具。然而,在神经科学中,可能性和模糊性的概念已被类似地用于衡量神经元、突触和其他大脑区域之间的协调程度。拟议的研究主题旨在满足对专用平台的需求,计算智能领域的专家可以齐聚一堂,讨论如何建模和传达神经成像数据处理中固有的不确定性。神经科学包含许多子领域,包括但不限于:计算神经科学;脑机接口;神经科学;神经信息学;神经人体工程学;计算认知神经科学;情感神经科学;神经生物学;脑映射;神经工程;神经技术。神经成像中使用的计算方法是本研究主题的主题,它探讨了各个学科的最新发展、问题和未来观点。因此,我们鼓励研究人员为本研究主题做出新的原创性贡献,利用神经成像中计算和数学技术的最新方法,应对为各种临床应用开发专用系统的挑战,并提出未来发展的新想法和方向。在这个研究主题中,来自不同领域的专家讨论了计算方法在神经成像中的当前发展、困难和潜在方向。本部分共提交了 26 篇文章,但只有 5 篇被选中进行审查。每篇提交的文章至少有两位审稿人和两轮审查。下面,我们简要概述了这些出版物各自的贡献。
海事系统设计与验证的形式化方法...
摘要 海上自主水面舰艇 (MASS) 正在接近现实,为海上控制系统带来了新的复杂性和关键性。在本文中,我们研究了如何使用形式化方法 (FM) 来设计和验证海上控制系统,以实现安全有效的 MASS。FM 是一系列基于数学的规范和验证方法。我们首先对 FM 进行高级介绍。我们讨论了当前的海上控制系统认证实践和走向自主化的需求。我们给出了三个具体示例,说明如何应用 FM 来满足这些需求:COLREG 的形式化规范、基于合同的设计和基于模拟的测试的自动化。最后,讨论了 FM 的一些局限性。我们得出结论,FM 似乎是满足部分自主性需求的有希望的候选者,并鼓励对 MASS 的 FM 进行进一步研究。关键词 海上自主水面舰艇、形式化方法、验证、规范、保证 简介 海上自主水面舰艇 (MASS) 正在接近现实,正在进行的项目众多,从小型研究原型到全尺寸工业船舶。虽然存在几种程度的自主性,但 MASS 的典型特点是能够在非平凡操作中独立于人类操作员运行,需要态势感知和规划能力。这些特点使得 MASS 开发人员需要新的设计方法,监管机构 (IMO 2021、NMD 2020) 和船级社 (DNV 2018) 也需要新的安全保证方法和流程。形式化方法 (FM) 是一类基于数学的规范和验证方法,源自理论计算机科学 (Woodcock 等人2009)。FM 提供高水平的保证,因此几十年来一直被积极用于其他行业(如航空航天和铁路)关键系统的开发和验证。随着自主系统的出现,FM 被认为是解决它们带来的一些保证挑战的有希望的候选者。这导致了过去十年来对应用于自动驾驶汽车和飞行器的 FM 的积极研究(Luckcuck 等人2019)。海运业尚未看到 FM 的广泛采用。然而,这种情况似乎正在改变,因为去年发表了一些文章。Shokri-Manninen 等人。福斯特等人。(2020) 创建了一个基于自动机的单船相遇正式模型,并综合了一种构造正确的导航策略。Park 和 Kim (2020) 基于可达性分析,综合了一种构造正确的船舶自动停靠控制器。(2020) 提出了一种混合动力系统形式的自主船舶控制器,并使用自动定理证明器来验证一些安全不变量。本文旨在通过首先进行高级介绍,引起海事界对 FM 的关注。接下来,我们回顾当前海事控制系统设计和验证的实践,并讨论一些走向自主化的需求。然后,我们在三个特定用例中激励并演示了 FM 的使用,以满足这些需求。最后,我们讨论一下 FM 的一些局限性。
法力和魔法定义及结点状态的模糊性
近年来,出现了许多论文讨论不同模型(如 CFT、结点理论等)的 magic 和 mana 属性 [1–3]。这些量表征此类模型中定义的某种量子力学状态与 Clifferd 群元素的距离 [4]。根据 Gottesmann-Knill 定理 [5],Clifferd 群元素可以在经典计算机上进行有效建模。因此,有人声称“magic”实际上是某种状态的非经典性,而 mana 则衡量这种非经典性。如果结合量子计算讨论这些属性,这些属性可能很重要。Gottesman-Knill 定理基于以下事实:Clifferd 群是所研究群 G 的一个有限子群,而 G 是几个 SU(N) 的张量积。然而,它并不是唯一的有限子群。对于同一个群 G ,可以定义无数个这样的子群。其中,克利福德群的定义性质是它与 sigma 矩阵的联系。从量子计算的角度来看,没有必要要求这一点。因此,根据想要向量子计算机呈现的问题集,可以对 mana 进行不同的定义。我们认为 mana 实际上是一种相对属性,而不是绝对属性。在本文中,我们将介绍克利福德群的通常定义方式以及如何对其进行修改以获得其他有限子群。我们将应用这个新的 mana 定义来研究结点状态。结点理论是一个被广泛研究的课题,与其他理论有很多关系。其中,结点理论与量子计算之间存在联系,它既提供了使用量子算法计算结点多项式的方法,也提供了将量子算法描述为有效拓扑场论中的一些结点配置 [14]- [19]。这涉及通过 Reshetikhin-Turaev 算法 [6]- [13] 使用酉矩阵计算结点。具体来说,对于某些特定的结点系列,任何量子算法都可以描述为一系列结点的连续近似 [18,19]。然而,在本文中,我们讨论了结点理论的不同方法。法力和魔法是量子态(密度矩阵)的属性,而不是酉运算。有一种方法可以定义对应于结点的量子态 [2],使用拓扑场论的思想 [20,21]。这个密度矩阵的矩阵元素由特殊点处的结点多项式构成。因此,这种状态的经典性为我们提供了有关如何在经典计算机上计算这些结点不变量的一些信息。论文组织如下。在第 2 章中,我们定义了 Clifferd 群,它是 SU ( N ) 群的一个有限子群。在第 3 章中,我们提供了 mana 的定义,就像其他关于该主题的论文(如 [1–3])中给出的那样。在第 4 章中,我们讨论了 mana 定义中的歧义,并展示了如何修改定义以给出与 SU ( N ) 的不同有限子群相关的 mana。在第 4 章中,我们根据 [2,20,21] 定义了描述不同结的量子力学状态。在第 5 章中,我们研究了结状态下的 mana 是什么样子,以及如何通过不同的 mana 定义来改变它。
过去定向标量场梯度和标量张量热力学
有多种动机将引力理论扩展到爱因斯坦广义相对论 (GR) 之外。所有将这一理论与量子物理相协调的尝试都会以额外场、高阶运动方程或高阶曲率不变量的形式引入与广义相对论的偏差。例如,取弦理论中最简单的玻色弦理论的低能极限,得到 ω = − 1 布兰斯-迪克理论,而不是广义相对论,后者是标量张量理论的原型(ω 是布兰斯-迪克耦合)[1,2]。然而,研究替代引力理论的最有力动机来自宇宙学。例如,最受数据青睐的膨胀模型,即斯塔罗宾斯基膨胀,包括对广义相对论的量子修正。最重要的是,基于广义相对论的标准冷暗物质宇宙学模型无法令人满意地理解当今宇宙的加速膨胀:它需要引入一个令人惊奇的精细调节的宇宙常数或另一种形式的特设暗能量,而暗能量的性质仍然难以捉摸[3]。无论如何,即使承认暗能量的存在,冷暗物质的其他问题仍然无法解决,如哈勃张力[4,5]、对同样神秘的暗物质的要求,以及困扰宇宙学和黑洞物理学的奇点问题。因此,研究其他引力理论来解决或缓解这些问题至少是合理的。修改广义相对论最简单的方法是增加一个标量(大质量)自由度,这导致了 Brans-Dicke 引力[6]及其标量-张量推广[7-10]。 f(R) 类引力理论原来是标量张量理论的一个子类,它在解释当前没有暗能量的宇宙加速过程中非常流行([11],参见[12-14]的评论)。在过去的十年中,旧的 Horndeski 引力 [15] 被重新审视并进行了深入研究(参见[16]的评论)。这类理论被认为是最一般的标量张量引力,允许二阶运动方程,但后来人们发现,如果满足合适的退化条件,更一般的退化高阶标量张量 (DHOST) 理论可以允许二阶运动方程(参见[17]的评论)。Horndeski 和 DHOST 理论在其作用中包含任意函数,这使得场方程非常繁琐,研究起来也很困难。多信使事件 GW170817/GRB170817 [ 18 , 19 ] 证实了引力波模式以光速传播,这基本上排除了结构最复杂的 Horndeski 理论 [ 20 ],但仍存在许多可能性(对应于作用中的四个自由函数)。因此,很难掌握这些理论及其解决方案的详细物理意义,并且大部分工作必然局限于形式理论方面和寻找分析解决方案。





![arXiv:2311.11218v1 [quant-ph] 2023 年 11 月 19 日](/simg/d\d7d33fa4e28ccabd530710ff87e02a66bfea49a4.webp)