XiaoMi-AI文件搜索系统
World File Search Systemprékopa -leindler不平等的定量稳定性结果
如上所述,优化器以Brunn -Minkowski和Prékopa -Leindler不平等现象而闻名。然而,尽管知道这些不平等的平等案例,但人们可能会问,如果一个人知道平等是“几乎”达到的,可以推论哪些几何特性。这通常称为稳定性估计。最近,已经获得了有关几何和功能不平等的各种重要稳定性结果。例如,Fusco,Maggi,Pratelli [28]证明了等等不等式的最佳稳定性版本。该结果扩展到各向异性等等不平等,以及figalli,Maggi,Pratelli [23,24]的Brunn – Minkowski不等式(对于后一种问题,目前的最佳估算是由于Koles-Nikov-Nikov,Milman,Milman,Milman [33])。可以进一步提及,例如,由Barthe,Böröczky,Fradelizi [5]提供了更强版本的Blaschke-Santaló不平等现象。由Ghilli,Salani [30],Rossi,Salani [42,43]和Balogh,Kristály[3]提供的Borell -Brascamp -Lieb不平等现象; Figalli,Zhang [26]的Sobolev不等式(扩展了Bianchi,Egnell [6]和Figalli,Neumayer [25]),Nguyen [38]和Wang [47]; Gozlan [31]的Log-Sobolev不平等现象;以及Caglar,Werner [12],Cordero-erausquin [15]和Kosov [32] Kolesnikov的一些相关不平等。Eldan [17,Lemma 5.2]获得了对数 - conconcave函数的prékopa-leindler不平等的“同构”的性结果。
prékopa -leindler不平等的定量稳定性结果
如上所述,优化器以Brunn -Minkowski和Prékopa -Leindler不平等现象而闻名。然而,尽管知道这些不平等的平等案例,但人们可能会问,如果一个人知道平等是“几乎”达到的,可以推论哪些几何特性。这通常称为稳定性估计。最近,已经获得了有关几何和功能不平等的各种重要稳定性结果。例如,Fusco,Maggi,Pratelli [28]证明了等等不等式的最佳稳定性版本。该结果扩展到各向异性等等不平等,以及figalli,Maggi,Pratelli [23,24]的Brunn – Minkowski不等式(对于后一种问题,目前的最佳估算是由于Koles-Nikov-Nikov,Milman,Milman,Milman [33])。可以进一步提及,例如,由Barthe,Böröczky,Fradelizi [5]提供了更强版本的Blaschke-Santaló不平等现象。由Ghilli,Salani [30],Rossi,Salani [42,43]和Balogh,Kristály[3]提供的Borell -Brascamp -Lieb不平等现象; Figalli,Zhang [26]的Sobolev不等式(扩展了Bianchi,Egnell [6]和Figalli,Neumayer [25]),Nguyen [38]和Wang [47]; Gozlan [31]的Log-Sobolev不平等现象;以及Caglar,Werner [12],Cordero-erausquin [15]和Kosov [32] Kolesnikov的一些相关不平等。Eldan [17,Lemma 5.2]获得了对数 - conconcave函数的prékopa-leindler不平等的“同构”的性结果。
arXiv:2002.12887v2 [quant-ph] 2020 年 9 月 9 日
摘要:借助量子信息论中的技术,我们开发了一种方法,可以系统地获得多个矩阵变量中的算子不等式和恒等式。它们采用迹多项式的形式:涉及矩阵单项式 X α 1 ··· X α r 及其迹 tr ( X α 1 ··· X α r ) 的多项式表达式。我们的方法依赖于将对称群在张量积空间上的作用转化为矩阵乘法。因此,我们将极化的凯莱-汉密尔顿恒等式扩展为正锥上的算子不等式,用 Werner 状态见证来表征多线性等变正映射集,并在张量积空间上构造置换多项式和张量多项式恒等式。我们给出了与量子信息论和不变理论中的概念的联系。
量子信息——硕士学位...
国家和团体。量子力学公理、量子比特、自旋-1/2、光子极化、密度算子、二分量子系统、布洛赫球、施密特分解、纠缠、集合解释的模糊性、凸性、集合的准备、比光还快?量子擦除、HJW 定理、两个量子态相距多远?、保真度和乌尔曼定理、距离测量之间的关系。措施和演变。正交测度及其他、正交测度、广义测度、量子通道、求和算子表示、可逆性、海森堡框架中的量子通道、量子运算、线性、完全正性、通道状态对偶和通道扩张、通道状态对偶、Stinespring 扩张、重新审视公理、三个量子通道、去极化通道、相移通道、振幅衰减通道、开放量子系统的主方程、马尔可夫演化、刘维尔、阻尼谐振子、非马尔可夫噪声、高斯相位噪声、自旋回波、量子比特作为噪声谱仪、非零温度下的自旋玻色子模型。量子纠缠。 EPR 对的不可分离性、隐藏量子信息、爱因斯坦局部性和隐藏变量、贝尔不等式、三个量子硬币、量子纠缠与。爱因斯坦局域性、其他贝尔不等式、CHSH 不等式、最大违反、量子策略优于经典策略、所有纯纠缠态都违反贝尔不等式、光子、实验和漏洞、使用纠缠、密集编码、量子隐形传态、量子隐形传态和最大纠缠、量子软件、量子密码学、EPR 量子密钥分发、无克隆、混合态纠缠、可分离性的部分正转置准则、无纠缠的非局域性、多方纠缠、量子三盒、猫态、纠缠增强通信、操纵纠缠。
相互无偏基的熵不确定关系的最优上界
2 | ⟨ ψ | [ A, B ] | ψ ⟩| 取决于初始状态,因此并不固定,以至于当 | ψ ⟩ 的某些选择时它会消失,这些选择不必是可观测量 A 和 B 的同时特征函数。此外,基于偏差的不确定性关系通常不能捕捉可观测量互补方面 [12] 的物理内容和信息内容的传播 [13]。用可观测量的熵来表示不确定性最早是由 Everett [17] 提出的。参考文献 [14] 对此进行了肯定的回答,即位置和动量可观测量的熵之和满足不等式。对于具有连续谱的可观测量,这种熵不确定关系分别在参考文献 [15, 16] 中得到证明和改进。当系统状态为高斯波包时,不等式的下界成立。熵不确定性关系在有限维希尔伯特空间中的可观测量的扩展最早在文献[11]中提出,后来在文献[18]中得到改进。我们希望
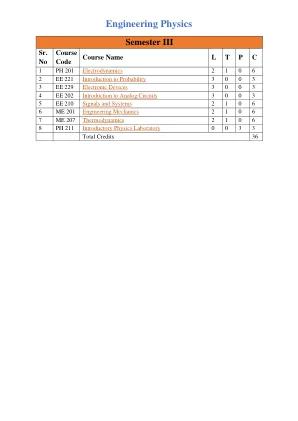
工程物理学
简介:学习本课程的动机、必修基础数学复习、实线子集上概率与长度的关系、概率形式定义、事件与$\sigma$代数、事件独立性与条件概率、事件序列与Borel-Cantell引理。随机变量:随机变量的定义、随机变量的类型、CDF、PDF及其性质、随机向量与独立性、随机变量变换简介、高斯随机向量简介。数学期望:通过例子了解平均值的重要性、期望的定义、矩与条件期望、MGF、PGF与特征函数的使用、方差与k阶矩、MMSE估计。不等式与收敛概念:马尔可夫、切比雪夫、切尔诺夫与Mcdiarmid不等式、概率收敛、均值与几乎必然、大数定律与中心极限定理。随机过程的简要介绍:示例和正式定义、平稳性、自相关和互相关函数、遍历性的定义。
使用UAV- ...
本文提出了一种集中式供应链网络优化模型,该模型最大化了一家生产和/或外包生产,商店,船只和出售产品的公司获得的总利润,并使用由卡车组成的机队,以及在最后一英里的船队中,也是无人机。该模型以无人机的形式包括无人机(UAV)的现实特征,其基本限制(例如电池容量低和交付范围较短)。受约束的非线性优化问题被提出为变异不等式。的存在和唯一性结果以及详细的数值模拟的结果提供了解决变化不等式的结果,这些模拟的结果强调了使用混合机队从增强利润到减少空气污染的优势。我们的定量结果揭示了物流行业的巨大希望和见解,即在整体供应链网络环境中使用新兴的无人机技术作为最后一英里包裹的实用解决方案。
教授Pantelimon George POPESCU - 量子 CS
90. PGPopescu,问题 XII.218[考虑 G 上的自同态全射得出 G 可交换],Revista Arhimede,5-8/2005,第 56 页。 91. PGPopescu,JLDiaz-Barrero,《某些零点和系数不等式》,《Archimede》杂志,nr. 5-8,2005,页2-6。 92. JLD´ıaz-Barrero,PGPopescu,凸函数的基本数值不等式,RGMIA - 研究报告集(在线和论文),2005,8(2):1-6,ISSN:1443-5764。 93. PGPopescu,问题 31,La Gaceta de la RSME,(第 8.1 卷(2005 年)),ISSN 1138-8927。 94. PGPopescu,《问题 37》,La Gaceta de la RSME,(第 8.2 卷(2005 年)),ISSN 1138-8927。 95. IVMaftei,PGPopescu,《问题 58》,La Gaceta de la RSME,(第 9.2 卷(2006 年)),ISSN 1138-8927。 96. IVMaftei,PGPopescu,《问题 68》,La Gaceta de la RSME,(第 9.3 卷(2006 年)),ISSN 1138-8927。 97. JLD´ıaz-Barrero,PGPopescu,《涉及复数多项式的一些恒等式》,RGMIA——研究报告集(在线和纸质),2006,9(2):1-6,ISSN:1443-5764。 98. JLD´ıaz-Barrero、JGB´aguena、PGPopescu,《涉及有理和的身份》,RGMIA - 研究报告集(在线和纸质),2006,9(4):1-5,ISSN:1443-5764。 99. PGPopescu,JLD´ıaz-Barrero,《凸函数的某些不等式》,《纯粹数学和应用数学不等式杂志》,2006,7(2):1-5,ISSN: 1443-5756。 100. JLD´ıaz-Barrero,PGPopescu,《某些平均值不等式》,《Octogon Mathematical Magazine》,Vol. 14,没有。 1,2006 年 4 月,页134-137,ISSN:1222-5657。 101. JLD´ıaz-Barrero,PGPopescu,问题 B-1025,Fibonacci Quarterly,(44 (4) : 371-371, 2006),ISSN:0015-0517。 102. JLD´ıaz-Barrero,PGPopescu,问题 U25,数学。反思,(5(2006))。 103. JLD´ıaz-Barrero,PGPopescu,问题 U26,数学。反思,(5(2006))。 104. JLD´ıaz-Barrero,PGPopescu,利用拉格朗日定理推导的不等式,Octogon数学杂志,第15卷。 15,没有。 1,2007 年 4 月,页80-83,ISSN:1222-5657。 105. JLD´ıaz-Barrero、JGB´aguena、PGPopescu,涉及中位数和三角形面积的不等式,Octogon数学杂志,第15卷。 15,没有。 2,2007 年 10 月,页725-729,ISSN:1222-5657。 106. JLD´ıaz-Barrero、PGPopescu,《指数不等式》,《Fibonacci Quarterly》,Vol. 45,没有。 3,2007,页279-280,ISSN:0015-0517。 107. PGPopescu,JLD´ıaz-Barrero,问题 B-1039,Fibonacci Quarterly,(45 (3) : 278-278, 2007),ISSN:0015-0517。 108. PGPopescu,JLD´ıaz-Barrero,问题 3269,Crux Mathematicorum 与数学混乱,(33 (6) : 367-367 (2007)),ISSN 1706-8142。 109. JLD´ıaz-Barrero,PGPopescu,问题 3281,Crux Mathematicorum 与数学混乱,(33 (7) : 429-429 (2007)),ISSN 1706-8142。 110. JLD´ıaz-Barrero,PGPopescu,问题 3282,Crux Mathematicorum 与数学混乱,(33 (7) : 429-429 (2007)),ISSN 1706-8142。 111. IVMaftei,PGPopescu,《问题 85》,La Gaceta de la RSME,(第 10.2 卷(2007 年)),ISSN 1138-8927。 112. JLD´ıaz-Barrero,PGPopescu,问题 120,La Gaceta de la RSME,(第 11.4 卷(2008 年)),ISSN 1138-8927。113. JLD´ıaz-Barrero,PGPopescu,问题 3313,Crux Mathematicorum with Mathematical Mayhem,(34 (2) : 104-104 (2008)),ISSN 1706-8142。114. JLD´ıaz-Barrero,PGPopescu,问题 H-674,Fibonacci Quarterly,(46/47 (3) : 283-283, 2009),ISSN:0015-0517。115. PGPopescu,JLD´ıaz-Barrero,斐波那契数的逆数之和,Fibonacci Quarterly,第 11.4 卷(2008 年)),ISSN:0015-0517。 46/47,第 1 期,2009 年,第 46 页。 88-89,ISSN:0015-0517。 116. PGPopescu,JLD´ıaz-Barrero,问题 3418,数学混乱的症结,(35 (2):111-111 (2009)),ISSN 1706-8142。 117. JLD´ıaz-Barrero,PGPopescu,问题 3539,数学混乱的症结,(36 (4) : 241-241 (2010)),ISSN 1706-8142。 118. PGPopescu, JLD´ıaz-Barrero,《涉及 π 和斐波那契数的不等式》,《斐波那契季刊》,第 48 卷,第 3 期,2010 年,第 286-286 页,ISSN:0015-0517。119. PGPopescu,JLD´ıaz-Barrero,《问题 B-1069》,《斐波那契季刊》,(48 (2) : 183-183,2010 年),ISSN:0015-0517。120. PGPopescu,JLD´ıaz-Barrero,《问题 B-1074》,《斐波那契季刊》,(48 (3) : 278-278,2010 年),ISSN:0015-0517。 121. JLD´ıaz-Barrero,PGPopescu,问题 1878,数学杂志,(84 (4) : 297-297 (2011)),ISSN:0025-570X。
使用不受信任的设备计算量子密码的安全密钥率
独立于设备的量子密钥分发 (DIQKD) 提供了最强大的安全密钥交换形式,仅使用设备的输入输出统计数据即可实现信息论安全性。尽管 DIQKD 的基本安全原理现已得到充分理解,但为高级 DIQKD 协议推导出可靠且强大的安全界限仍然是一项技术挑战,这些界限要超越基于违反 CHSH 不等式而得出的先前结果。在这项工作中,我们提出了一个基于半有限规划的框架,该框架为使用不受信任设备的任何 QKD 协议的渐近密钥速率提供可靠的下限。具体而言,我们的方法原则上可用于基于完整输入输出概率分布或任何贝尔不等式选择来为任何 DIQKD 协议找到可实现的密钥速率。我们的方法还扩展到其他 DI 加密任务。
准随机量子信道
与图相关的自然过渡矩阵的混合(或准随机)属性可以通过其与完全图的距离来量化。不同的混合属性对应于测量此距离的不同范数。对于密集图,Chung、Graham 和 Wilson 在 1989 年的开创性工作中证明了两个这样的属性(称为谱扩展和均匀性)是等价的。最近,Conlon 和 Zhao 使用著名的 Grothendieck 不等式将这种等价性扩展到稀疏顶点传递图的情况。在这里,我们将这些结果推广到非交换或“量子”情况,其中过渡矩阵成为量子信道。特别是,我们表明,对于不可约协变量子信道,扩展等同于图的均匀性的自然类似物,推广了 Conlon 和 Zhao 的结果。此外,我们表明,在这些结果中,非交换和交换的格罗滕迪克不等式产生了最佳常数。



![arXiv:2002.12887v2 [quant-ph] 2020 年 9 月 9 日](/simg/2\266fcfc90101fc10fe1a8b82fd7ef6ff26d4692f.webp)