XiaoMi-AI文件搜索系统
World File Search System强磁化旋转偶极子中的粒子加速和辐射反应
背景。中子星被超强电磁场有效加速的超相对论粒子所包围。这些粒子通过曲率、同步加速器和逆康普顿辐射大量发射高能光子。然而,到目前为止,还没有任何数值模拟能够处理这种极端情况,即非常高的洛伦兹因子和接近甚至超过量子临界极限 4.4 × 109T 的磁场强度。目的。本文旨在研究旋转磁偶极子中的粒子加速和辐射反应衰减,其实际场强为 105 T 至 1010 T,这是毫秒和年轻脉冲星以及磁星的典型场强。方法。为此,我们在简化的 Landau-Lifshitz 近似中实现了一个精确的分析粒子推动器,包括辐射反应,其中假设电磁场在一个时间步长积分期间在时间上恒定而在空间上均匀。使用速度 Verlet 方法执行位置更新。我们针对时间独立的背景电磁场(如交叉电场和磁场中的电漂移以及偶极子中的磁漂移和镜像运动)对我们的算法进行了广泛的测试。最后,我们将其应用于真实的中子星环境。结果。我们研究了粒子加速以及辐射反应对插入毫秒脉冲星、年轻脉冲星和磁星周围的电子、质子和铁核的影响,并与没有辐射反应的情况进行了比较。我们发现最大洛伦兹因子取决于粒子种类,但与中子星类型的影响很小。电子的能量高达 γ e ≈ 10 8 − 10 9 ,而质子的能量高达 γ p ≈ 10 5 − 10 6 ,铁的能量高达 γ ≈ 10 4 − 10 5 。虽然质子和铁不受辐射反应的影响,但电子的速度却急剧下降,使其最大洛伦兹因子降低了四个数量级。我们还发现,在几乎所有情况下,辐射反应极限轨迹都与简化的朗道-利夫希茨近似非常吻合。
具有碱土金属一氧化物和一硫化物阳离子的偶极子声子量子逻辑
在所有量子系统中,囚禁离子量子比特已证明具有最高保真度的量子操作 1–4 。因此,如果能够应对集成和扩展相关技术的挑战,它们将成为可扩展量子信息平台的有希望的候选者。这些挑战中最主要的是这种激光器的集成,这不仅是冷却离子所必需的,而且通常也是操纵量子比特所必需的。目前,正在研究两种主要方法来解决这个问题。首先,如果硅光子学中展示的能力可以扩展到与原子离子量子比特所需的可见光和紫外波长兼容的材料,那么集成光子学可以提供一种可扩展的方式来传输必要的激光器 5,6 。其次,人们正在探索几种无激光操控原子离子量子比特的方案,这些方案涉及微波场与强静态磁场梯度 8-10、微波磁场梯度 11-13、微波修饰态 14 或运动模式频率附近振荡的磁场梯度 15,16 的配对。集成光学和微波控制都需要离子阱制造技术的进步才能真正实现可扩展性。
Chern,偶极子和四极杆拓扑阶段,具有方形晶格和非常规单位单元格
用于研究光子学中的拓扑阶段,而量子 - 大实型型前一阶手性边缘状态通常在磁光光子晶体中实现,而高阶拓扑状态大多在全dielectric光子晶体中探索。在这项工作中,我们研究了磁光子光子晶体中的一阶和二阶拓扑光子状态。在特定的情况下,我们在一个平方晶格中重新访问一个简单的磁光子光子晶体,每个单元中有一个旋风磁缸。However, rather than investigating the conventional unit cell where the cylinder is at the center of the square unit cell as previous works have done, we consider a configuration where the cylinders are located at the four corners of the square unit cell and show that this configuration hosts rich topological phases, such as dual-band Chern, dipole, and quadrupole topological phases.我们对这些拓扑状态的详细特征基于Wannier带和它们通过Wilson Loop和Nested Wilson Loop方法的极化。我们详细研究了不同拓扑阶段的边缘和角状态,并表明它们具有“频谱鲁棒性”的特殊特征。例如,尽管生活在带隙中的偶极相的边缘和角状态可以通过调谐边界条件将其推入散装带,但它们可以通过散装带并在不同的带隙内重新出现。对于双波段四极阶段,我们可以找到一个政权,两个乐队差距同时容纳了一组角状态,并且有趣的是,一组角状状态的填充异常可以使它们的签名在另一组拐角处的异常状态中,尽管它们被广泛的国家数量占据了一个拐角处。在简单的磁光子光子晶体中揭示的丰富拓扑物理学不仅为时间反转对称性折叠光子系统提供了对高阶拓扑阶段的新见解,结果还可以通过利用边缘和角状态的电势来找到有希望的应用。
在 Dzyaloshinskii–Moriya 相互作用下使用量子记忆实现两个耦合偶极子自旋的熵不确定性
1 艾资哈尔大学理学院物理系,艾斯乌特 71524,埃及;ANkhedr@azhar.edu.eg (ANK);amabdelaty@ub.edu.sa (A.-HA-A.);tammam@azhar.edu.eg (MT) 2 萨坦·本·阿卜杜勒阿齐兹王子大学阿夫拉杰科学与人文学院数学系,沙特阿拉伯阿夫拉杰 11942 3 艾斯乌特大学理学院数学系,艾斯乌特 71515,埃及 4 比沙大学理学院物理系,比沙 61922,沙特阿拉伯 5 索哈杰大学理学院数学系,索哈杰 82524,埃及; mabdelaty@zewailcity.edu.eg 6 沙迦大学应用物理与天文学系,沙迦 27272,阿拉伯联合酋长国;heleuch@sharjah.ac.ae 7 阿布扎比大学艺术与科学学院应用科学与数学系,阿布扎比 59911,阿拉伯联合酋长国 8 德克萨斯 A&M 大学量子科学与工程研究所,德克萨斯州大学城 77843,美国 * 通讯地址:abdelbastm@aun.edu.eg
扩展了分子集合的Tavis – Cummings模型 - 探索偶极子自我能量和静态偶极矩的效果
有机分子与纳米级腔的真空场的强耦合可用于修饰其化学和物理性质。我们扩展了分子集合的Tavis – Cummings模型,并表明,静态偶极矩和偶极子自我能量产生的经常被忽视的相互作用术语对于正确描述了极化化学中的光 - 肌肉交互作用至关重要。在完整的量子描述的基础上,我们模拟了MGH +分子的激发态动力学和光谱,并共偶联与光腔。我们表明,对于获得一致的模型来说,必须包含静态偶极矩和偶极子自我能量。我们构建了一种有效的两级系统方法,该方法重现了真实分子系统的主要特征,可用于模拟较大的分子集合。
DOI: 10.29026/oea.2023.220154 用于光发射和光检测的无 ITO 硅集成钙钛矿电化学电池
第 2 部分:钙钛矿层光提取方向模拟细节考虑到 PeLEC 在自发发射模式下运行,我们考虑将一个方位角可变超过 360°(计算期间)的光学点偶极子放置在钙钛矿层内作为发光源。在 SI 图 S1(a) 中,有一个 PeLEC 的光发射提取曲线与点偶极子方向的组合,其中沿基底表面(即在小角度下)实现了最大提取效率,约为 13%。随着点偶极子方向角度的增加,提取效率急剧下降。根据发射光电场矢量模量图,参见 SI 图 S1(b),对于对提取效率贡献最大的较小角度(< 45°),观察到类似于各向同性的角度分布。在这种情况下,我们能够对点偶极子方向角上的提取效率进行平均,并确定平均提取效率,考虑到方位角,平均提取效率为 9.2%。因此,实验观察到的数据可以通过以下假设来解释:大部分 PeLEC 的光发射都被 Si 基板吸收。
积极的青年发展STEM学会使用力量! ...
现在我们了解电力,让我们讨论磁铁。磁铁是产生磁场的材料。磁场是看不见的,但负责拉动其他铁磁材料(例如铁或钢)的力。仅使用铁磁材料(例如钢)可以用作磁铁。这是因为材料内部有偶极子,可以将其对齐。偶极子是具有正电荷和负电荷区域的分子。当偶极对齐时,它会产生一个磁场。我们将材料的一侧称为北极,另一侧是南极。并非所有材料都有此特性,因此并非所有材料都可以是磁铁。在永久性磁铁中,偶极子始终对齐,因此材料总是在创建磁场(您看不到字段)。例如,冰箱磁铁是永久磁铁。
讲座 6 吸收与光生成
原子移离平衡位置后,原子核会从电子云中移开。光子的电场会与原子核(电子云偶极子)产生共振(场是附加的),从而被吸收。硅、锗等共价材料往往是较差的光吸收剂。需要晶格振动才能在晶体中诱导偶极子,然后光才能被吸收=间接间隙。
第 8 讲状态方程、平衡和爱因斯坦......
原子移离平衡位置后,原子核会从电子云中移开。光子的电场会与原子核(电子云偶极子)产生共振(场是附加的),从而被吸收。硅、锗等共价材料往往是较差的光吸收剂。需要晶格振动才能在晶体中诱导偶极子,然后光才能被吸收=间接间隙。
了解脑电图来源定位的有用性
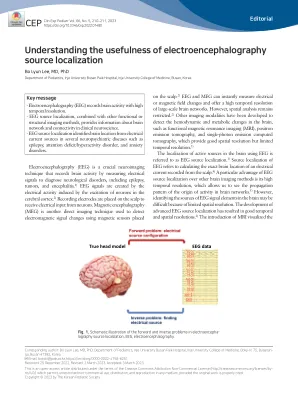
基于EOM的审查,源本地化过程必须解决前进和反问题(图1)。1,3,5,6)远期问题是当前来源对头皮电势的期望,可以通过准确的头部模型来解决。1,3,5)脑组织的形状和传导分布强烈影响脑电图信号。因此,应使用个性化的MRI来构建确切的头部模型并实现更精确的源定位。4)反问题是指使用头皮电势测量值估算大脑中电流源的精确位置。1)解决此问题的一种方法是使用有关体积导体和发电机解剖结构的合理假设来设定局限性。已经引入了有关反问题的几个建议。1,2,4,5)尤其是作者描述了源分析模型的方法,例如偶极源定位和分布式源定位。从头皮脑电图记录的偶极子源定位可以通过计算当前偶极子的位置,方向和矩参数来估计位置源。4,7)然而,偶极子源定位需要先验假设大脑中的几个活动区域,假定有限数量的等效偶极子,并且可能会因缺失的偶极子而产生偏见。4,5)脑成像方法的最新发展导致了更复杂的选项,可以从头皮EEG信号中定位大脑来源,目前使用了几种分布式源定位方法。4,5,8)4,5)最受欢迎的分布式源模型是最低规范解决方案的修改算法,例如加权最小规范解决方案,低分辨率电磁断层扫描和局部自回旋平均值。