XiaoMi-AI文件搜索系统
World File Search System应用物理学研究生课程的教学大纲
详细信息第一学期MPYC-101(经典力学)标记100单位I:粒子系统的力学:惯性和非惯性框架的参考框架。拉格朗日公式,速度依赖性电位和耗散功能,守恒定理和对称特性,空间的HO形成性和各向同性以及线性和角度动量的守恒,时间和能量的均匀性。Hamiltonian Formulation: Calculus of variations and Euler Lagranges equation, Brachistochrone problem , Hamiltons principle, extension of Hamiltons principle to nonholonomic systems , Legendre transforma-tion and the Hamilton equations of motion, physical significance of Hamiltonian ,Derivation of Hamiltons equations of motion from a variational principle , Rouths procedure , Principle of least action.(12)单元-II:规范转换:规范转换,生成功能的类型,规范转换的条件,庞美列的整体不变性,Poissons Theorem,Poisson和Lagrange Bracket,Poisson和Poisson和Lagrange括号,作为典型的Infitites Invarities Invarities Invarities Invarity Invarise Invarient anderical Transferations Theoremations theorems,liounion theorems,liou nou。汉密尔顿-Jacobi理论:汉密尔顿 - 汉密尔顿主管功能,谐波振荡器和开普勒问题的雅各布方程 - 汉密尔顿 - 雅各比方法,雅各比方法,完全可分离的系统的动作角度变量,开普勒系统中的开普勒问题在动作角度变量,地球光学和波浪机制。(15)单位-III:小振荡:小振荡的问题,两个耦合振荡器的示例,小振荡的一般理论,正常坐标和正常的振动模式,线性截然分子的自由振动。刚体运动:独立于刚体的坐标,正交转换,欧拉角,Cayley-Klein参数,欧拉斯对刚性体运动,无限旋转,载体的变化速率,coriolis力量的效力。刚体动力学:一点点运动的角动量和动能。:惯性和惯性动量,惯性张量的特征值和主要轴变换。重对称顶部具有一个点固定的。关于非线性和混乱的质量。(13)书籍:1。古典力学H. Goldstein 2。古典力学-Landau和LiftShitz 3。古典力学Corben&Stehle 4。古典动态Marion&Thornton 5。分析力学L. Hand和J. Finch 6。经典力学J.C. UPADHYAYA MPYC-102(Physics-I中的数学方法)完整标记-100单元I复杂分析:简要修订复数及其图形表示。Euler的公式,De Moivre的定理,复数的根。复杂变量的功能。分析性和cauchy-riemann条件。分析功能的示例。奇异函数:杆和分支点,奇异性的顺序,分支切割。集成一个复杂变量的函数。Cauchy'sInquality.cauchy的积分公式。简单和
分子对接单元5:QSAR统计方法Dr.D....
许多配体的灵活性使得这些计算变得困难,需要开发和使用特殊方法。以下两个例子说明了对此类工具的需求:蛋白酶抑制剂的设计和与特定 MHC 受体结合的肽抗原的分析和设计。我们回顾了从刚体对接扩展到柔性对接的计算概念,以及以下重要的柔性对接和设计策略:(a) 蒙特卡洛/分子动力学对接,(b) 现场组合搜索,(c) 配体构建,以及 (d) 位点映射和片段组装。讨论了使用经验自由能作为目标函数。由于方法学的快速发展,大多数新方法仅在有限数量的应用上进行了测试,并且可能会改进更传统的计算或图形工具获得的结果。
无人机惯性在线测量...
动力学模型及其参数的辨识是机器人技术和系统动力学建模领域的基本问题之一。对于物体具有六个自由度 (6-DOF) 的一般情况,例如无人机 (UAV) 的情况,关键物理参数是飞行器质量和转动惯量。尽管无人机质量及其几何/拓扑结构很容易获得,但考虑到惯性张量无法通过静态试验测量,因此很难辨识。本文介绍了一种基于双线摆和机载集成传感器系统的简单有效的刚体惯性在线估计方法。其中,测试对象(即无人机)由两根细平行线悬挂,形成绕垂直轴的双线扭摆。使用无人机飞行控制器 (FC) 单元的机载传感器记录和处理摆锤振动,以获得用于最终惯性估计阶段的无趋势和无噪声信号。针对与无人机控制箱和完整无人机配置相关的两个典型悬浮物体案例,通过实验验证了所提出的识别算法。
高空长航时容错控制
摘要:高空长航时 (HALE) 飞机由极轻的结构、大翼展和大纵横比组成。这些特性的组合导致飞机系统具有独特的动态行为,其特点是结构和刚体特征模态的强烈相互作用。这些特性对此类飞机的飞行控制算法的稳健性和容错性提出了特定要求。控制系统必须能够让飞机安全地沿着定义的轨道飞行,即使在发生故障的情况下也是如此。由于这些飞机的尺寸较大,它们通常会过度驱动,具有多个冗余控制面。本文利用这种冗余来设计容错控制系统,以确保在故障情况下实现最佳控制性能。该策略基于故障检测和隔离 (FDI) 算法来检测故障的控制面。此故障信息用于在多模型控制方法中切换到备用控制律。FDI 滤波器是使用基于零空间的设计范例设计的,而备用控制器是应用结构化 H ∞ 控制设计技术合成的。
火箭发射器的主动姿态控制
由于运载火箭的性能与其飞行控制系统密切相关,因此航天飞行中的一个重大挑战是设计姿态控制算法,以确保运载火箭的稳定性,同时遵循确定的轨迹并抑制外界干扰。本报告旨在描述设计这种控制算法并最终评估其性能的通用方法。首先,回顾了现有的姿态控制方法并介绍了线性控制理论。然后介绍影响运载火箭的重要现象,包括刚体动力学、空气动力学、发动机惯性、下垂模式和弯曲模式。然后,使用给定的案例研究作为示例来估计描述所有这些现象的参数。然后推导线性运动方程,并提出构建车辆及其执行器的状态表示的方法。基于该线性模型,本文描述了一种逐步方法来计算用于处理所有相关现象的稳定 PID 控制器。最后,进行包括稳定性、时间响应、灵敏度和鲁棒性在内的性能分析,以评估控制器行为。
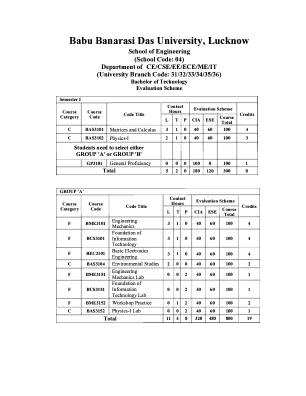
巴布·巴纳拉西达斯大学,勒克瑙
>s lurncnt,I lnlroJut。:tion,剪切力和D�1h.l i ng剪切力和弯矩的微分方程,静定梁的剪切力和弯矩图。桁架:介绍,简单桁架和简单桁架的解决方案,截面法;接头法;如何确定构件是处于拉伸还是压缩状态;简单桁架;零力构件质心和惯性矩:介绍,平面,曲线,面积,体积和复合体的质心,平面面积的惯性矩,平行轴定理和垂直轴定理,复合体的惯性矩。运动学和动力学:线性运动、瞬时中心、达朗贝尔原理、刚体旋转、冲量和动量原理、功和能量原理。简单应力和应变:应力的定义、应力张量、轴向载荷构件的法向应力和剪应力、应力-应变关系、延性和脆性材料单轴载荷的应力-应变图、胡克定律、泊松比、剪应力、剪应变、刚度模量、弹性常数之间的关系。不同横截面构件的一维载荷、温度应力、应变能。
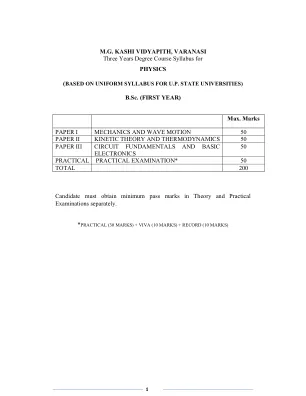
瓦拉纳西的喀什维迪亚皮特
试卷 I - 力学与波动 第一单元 惯性参考系、牛顿运动定律、直线和圆周运动中粒子的动力学、保守力和非保守力、能量守恒、线性动量和角动量、一维和二维碰撞、横截面。 第二单元 简单物体的转动能量和转动惯量、刚体在水平和倾斜平面上的平动、转动和运动的综合、陀螺运动的简单处理。弹性常数之间的关系、梁的弯曲和圆柱体的扭转。 第三单元 中心力、两粒子中心力问题、减小质量、相对和质心运动、万有引力定律、开普勒定律、行星和卫星的运动、地球静止卫星。 第四单元 简谐运动、SHM 的微分方程及其解、复数符号的使用、阻尼和强迫振动、简谐运动的合成。波动的微分方程、流体介质中的平面行进波、波的反射、反射时的相变、叠加、驻波、压力和能量分布、相速度和群速度。
气动弹性运载火箭的晃动观测器设计
本文重点介绍滑模观测器的设计,以估计晃动质量的位置和速度状态。这些状态随后用作姿态控制器的反馈信号。简单的比例微分 (PD) 刚体控制器无法安全地执行姿态命令,否则会遇到稳定性问题,即使在稳定状态下,非零晃动质量位置也会导致旋转角度抖动。通过晃动状态反馈,即使是非最优 PD 控制器也会在有限的执行器活动下表现出平滑的响应。然而,观测器的晃动模型参数的轻微不确定性会对控制器性能产生负面影响,从而增加液体的振幅和振荡行为。需要额外的观测器来估计正确的参数值。更强大的增量非线性动态逆控制器可以改善控制器响应,但需要进一步开发,例如,在反馈回路中加入陷波滤波器。
飞行路径重建滤波器扩展,用于灵活跟踪...
I. 简介 飞行测试是任何新型飞机开发过程的核心部分。作为测试的一部分,记录飞机在各种机动过程中的响应,从中可以确定描述其特性的飞机稳定性系数。然后可以使用这些估计值来验证或更新现有的数值模型。但是,测量到的响应有噪声、有偏差,并且可能以不同的速率采样,这可能导致模型不准确。因此,在估算这些稳定性系数之前,飞行路径重建 (FPR) [ 1 , 2 ] 通常是过滤和检查收集的飞行测试数据的一致性的第一步。FPR 是一种过滤技术,通过将飞机运动方程与响应测量相结合来重建飞机状态的时间历史。在这些方程中,飞机被表示为在空中移动的点质量。然而,为了提高燃油效率,飞机结构变得更轻,从而也更灵活。这反过来导致飞机的结构动力学与飞机飞行动态响应具有更大的相互作用。因此,为了正确地模拟这种相互作用,还需要重建结构的动力学和刚体状态。除了气动弹性建模外,跟踪飞机结构变形对于结构等应用也很重要
在存在的情况下进行多体量子态控制......
量子态控制对于量子信息处理和通过量子网络传输量子信息至关重要。在本文中,我们研究如何通过设计描述系统内部几何形状或配置的时间相关物理参数来控制多体量子系统的时间演化。一个有趣的经典类比是,一只坠落的猫可以重新调整自己的方向,以便它四脚着地,最大限度地减少对身体的伤害[1-4]。这种经典现象的可控性与这样一个事实有关:猫不是刚体[5],但可以改变身体的形状和身体各部分的相对方向,使它能够在不违反角动量守恒定律的情况下旋转。在量子领域,自主控制问题可能变得更加复杂,因为量子变形体并不是一个经过充分研究的、能够轻易表现出量子控制特性的平台。为了说明我们的方法,我们考虑一个由耦合谐振子链组成的量子系统,我们将使用它来展示在给定的控制运行时间内通过改变耦合和频率来实现量子猫态的传输和重新定位。